РАСЧЕТ ПЕРЕДАЧИ ЛАЗЕРНОЙ ЭНЕРГИИ СТРАТОСФЕРНОМУ МНОГОЦЕЛЕВОМУ ДИРИЖАБЛЮ ИЗ ЛАЗЕРА КОСМИЧЕСКОГО БАЗИРОВАНИЯ
Базухаир Мохаммед Ахмед
Бакалавр,
Казанский национальный исследовательский технический университет им. А. Н. Туполева – КАИ
РАСЧЕТ ПЕРЕДАЧИ ЛАЗЕРНОЙ ЭНЕРГИИ СТРАТОСФЕРНОМУ МНОГОЦЕЛЕВОМУ ДИРИЖАБЛЮ ИЗ ЛАЗЕРА КОСМИЧЕСКОГО БАЗИРОВАНИЯ
Аннотация
В данной статье рассматривается математическая модель передачи лазерной энергии стратосферному дирижаблю, характеризуемому подвешенным полетом, из лазера космического базирования, установленного на геостационарной орбите. Концепция получила название лазерного стратосферного многоцелевого дирижабля (ЛСМД).
Ключевые слова: лазерный ЛА, беспроводная передача энергии ЛА, лазерный дирижабль, стратосферный дирижабль.
Bazuhair Mohammed Ahmed
Bachelor,
Kazan National Research Technical University named after A. N. Tupolev - KAI
CALCULATION OF LASER ENERGY TRANSMISSION FROM SPACE-BASED LASER TO MULTIPURPOSE STRATOSPHERIC AIRSHIP
Abstract
In this paper, we view a mathematical model of laser energy transmission to a hovering stratospheric airship supplied by space-based laser positioned on the geostationary orbit. This concept became called as multipurpose stratospheric laser airship (MPSLA).
Keywords: laser aerial vehicle, aerial vehicle with wireless power transmission, laser airship, stratospheric laser dirigible.
Определение интенсивности лазерного излучения
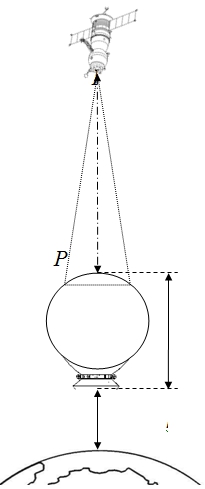
Рис. 1 - постановка предложенной системы в пространстве, показывающая способ передачи электроэнергии ЛСМД
Здесь R=35756 км, h = 30 км
Наиболее точно определить падающую мощность Pпад, посылаемую от лазера космического базирования (ЛКБ), можно через вычисление мощности лазерного луча на граничном слое атмосферы до того момента, когда его исходная мощность Po начнет гаситься пропорционально пути L вследствие ослабляющих лазерный луч факторов. Так как [1]![]() (1)
(1)
Здесь ![]() – радиус солнечной панели ЛСМД; Aф – площадь одного фотоэлемента в солнечной панели;
– радиус солнечной панели ЛСМД; Aф – площадь одного фотоэлемента в солнечной панели; ![]() – мощность одного фотоэлемента;
– мощность одного фотоэлемента; ![]() – коэффициент полезного действия солнечной панели, используя формулу интенсивности лазерного луча ϕ с учетом ослабляющих факторов в атмосфере, получим [3]
– коэффициент полезного действия солнечной панели, используя формулу интенсивности лазерного луча ϕ с учетом ослабляющих факторов в атмосфере, получим [3]
![]() (2)
(2)
где ε – коэффициент затухания лазерного луча в изучаемой среде; L – расстояние от термосферы до высоты ![]() (см. рис 1);
(см. рис 1); ![]() – коэффициенты дифракции, турбулентности, дрожания и расплывания, последовательно, характеризующие ослабление мощности Po лазерного луча вдоль пути L, см. [3]. Условия и параметры в атмосфере изменяются с изменением высоты h, где в некоторых слоях они начинают колебаться между положительными и отрицательными значениями температуры T и т.п., что требует их учесть.
– коэффициенты дифракции, турбулентности, дрожания и расплывания, последовательно, характеризующие ослабление мощности Po лазерного луча вдоль пути L, см. [3]. Условия и параметры в атмосфере изменяются с изменением высоты h, где в некоторых слоях они начинают колебаться между положительными и отрицательными значениями температуры T и т.п., что требует их учесть.
В наших расчетах принята высота полета, равная h = 30000 м от уровня моря, т.е. путь лазерного луча до ряда фотоэлементов дирижабля равен L=120–30 = 90000 м.
Итак, количество лазерного луча, потерянного из-за дифракции, можно вычислить следующим образом [3]
![]() (3)
(3)
где B – качество луча; λ– длина волны лазерного луча; ![]() – наименьший диаметр пятна от луча на формирующей оптике, причем
– наименьший диаметр пятна от луча на формирующей оптике, причем ![]() .
.
Коэффициент затухания ε разных волн при проникновении лазерного луча вплоть до ряда фотоэлементов резко отличается в зависимости от длины волны λ и присутствия пара и аэрозоля в атмосферной среде. Зависимость ε от его составляющих ![]() и
и ![]() записывается в виде [3][5]
записывается в виде [3][5]
![]() (4)
(4)
Поскольку пары и аэрозоли не существуют на рассматриваемой нами высоте вдоль L, то ε можно пренебречь для упрощения основных расчетов. Большая высота h повышает экономичность передачи энергии излучения, так как потеря передаваемой мощности при этом наименьшая.
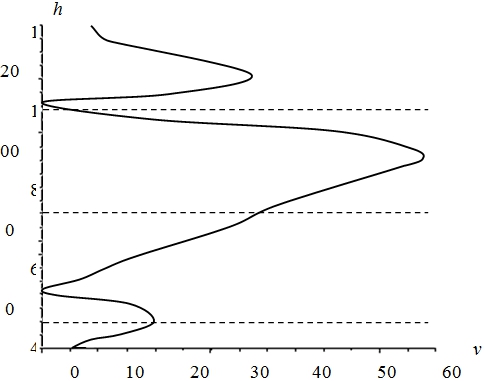
Метеорологические исследования показывают, что чем выше подняться в атмосферу, тем сильнее будут ветра и турбулентность из-за тепловой конвекции на высотах 7-10 км и 65-70 км, где происходят так называемые струйные течения со скоростью от 108 км/ч до 250-350 км/ч, имеющие крупные пространственные размеры [1]. Луч, проходящий через атмосферную среду, подвергается турбулентности, которая в максимуме достигает 63 м/с как показано на рис. 2.
Рис. 2 - изменение скорости ветра в атмосфере
Следовательно, значение постоянной атмосферной структуры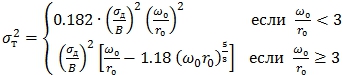 (5)
(5)
Выбор той или иной условной формулы требует нахождение параметра Фреда ro, заданного в следующем виде [3]
![]() (6)
(6)
где k – постоянная распространения волны, равная![]() ;
; ![]() – угол Зенита, который записывается так [2]
– угол Зенита, который записывается так [2]
![]() (7)
(7)
где φ – это местная широта; γ – часовой угол по местному солнечному времени; ![]() – текущее отклонение Солнца, которое можно определить в любой день года N из формулы [4]
– текущее отклонение Солнца, которое можно определить в любой день года N из формулы [4]
![]()
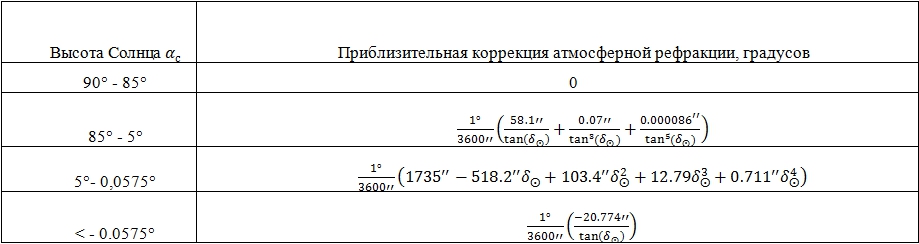
Стоит отметить, что данная формула только определяет теоретическую координату Солнца без учета влияния атмосферной рефракции. Для коррекции погрешности при определении наблюдаемого отклонения Солнца можно использовать следующую таблицу 1, где высота солнцa ![]() рассчитывается с помощью выражения [2][4]:
рассчитывается с помощью выражения [2][4]:
![]()
Таблица 1 - формулы вычисления приблизительной коррекции атмосферной рефракции
Как известно, постоянная атмосферной структуры ![]() имеет неизменную величину в случае прохождения лазерного луча по горизонтали. Однако нам необходимо, по ходу решения уравнения Фреда, найти интеграл функции изменения высоты L, начиная с высшего слоя L ≥ 90000 м до
имеет неизменную величину в случае прохождения лазерного луча по горизонтали. Однако нам необходимо, по ходу решения уравнения Фреда, найти интеграл функции изменения высоты L, начиная с высшего слоя L ≥ 90000 м до ![]() [3]
[3]
![]() (8)
(8)
где W – коэффициент корреляции ветра.
В лазерах высокой мощности коэффициент дрожания ![]() , влияние которого возникает из-за вибрации лазера и его оптики, составляет 4-6μрад [3]. Лазер космического базирования (ЛКБ), вращающийся на геостационарной орбите, находится под воздействием ряда сил (возмущений), изменяющих параметры этой орбиты. В частности, к таким возмущениям относятся гравитационные лунно-солнечные возмущения, влияние неоднородности гравитационного поля Земли, эллиптичность экватора и т.д. Деградация орбиты выражается в двух основных явлениях:
, влияние которого возникает из-за вибрации лазера и его оптики, составляет 4-6μрад [3]. Лазер космического базирования (ЛКБ), вращающийся на геостационарной орбите, находится под воздействием ряда сил (возмущений), изменяющих параметры этой орбиты. В частности, к таким возмущениям относятся гравитационные лунно-солнечные возмущения, влияние неоднородности гравитационного поля Земли, эллиптичность экватора и т.д. Деградация орбиты выражается в двух основных явлениях:
- ЛКБ смещается вдоль орбиты от своей первоначальной орбитальной позиции в сторону одной из четырёх точек стабильного равновесия, так называемых «потенциальных ям геостационарной орбиты» (их долготы 75,3°E, 104,7°W, 165,3°E, и 14,7°W) над экватором Земли;
- наклонение орбиты к экватору увеличивается (от первоначального 0) со скоростью и достигает максимального значения 15 за 26,5 лет.
Для компенсации этих возмущений и удержания конструкции в заданной точке ЛКБ оснащается двигательной установкой (химической или электроракетной).
В итоге, мы подбираем наименьшую величину ![]() , так как орбитальное дрожание не происходит интенсивно за малый промежуток времени t, что способствует уменьшению его влияния в краткосрочном периоде.
, так как орбитальное дрожание не происходит интенсивно за малый промежуток времени t, что способствует уменьшению его влияния в краткосрочном периоде.
При проникновении лазерного луча через любую, в том числе атмосферную, газовую среду температура столба луча, т.е. воздуха ![]() , характеризуется последовательностью её температурной концентрации. В середине столба газовые частицы имеют высокую температуру
, характеризуется последовательностью её температурной концентрации. В середине столба газовые частицы имеют высокую температуру ![]() , что приводит к уменьшению их местной плотности
, что приводит к уменьшению их местной плотности ![]() , а с другой стороны, граничные частицы обладают меньшей температурой
, а с другой стороны, граничные частицы обладают меньшей температурой ![]() , соответственно, большой местной плотностью
, соответственно, большой местной плотностью ![]() . В результате этого явления расфокусируется часть луча, т.е. происходит расплывание вокруг столба лазерного луча. Величина этого теплового расплывания
. В результате этого явления расфокусируется часть луча, т.е. происходит расплывание вокруг столба лазерного луча. Величина этого теплового расплывания ![]() определяется из выражения [3]
определяется из выражения [3]
![]() (9)
(9)
где коэффициент, учитывающий потерю при проникновении в атмосферную среду равен ![]() , а коэффициент ψ, в свою очередь, равен [3]
, а коэффициент ψ, в свою очередь, равен [3]
(10)
Причем коэффициенты пропорциональности ![]() и определяются следующими соотношениями [3]
и определяются следующими соотношениями [3]
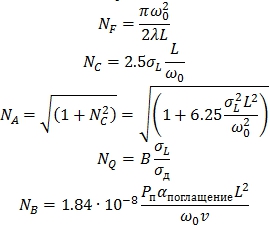
Следует отметить, что одним из параметров, влияющих на тепловое расплывание лазерного луча ![]() , является скорость течения v частиц газовой среды, через которую проникает луч (см. рис.2). Однако маленькая плотность высоких слоев атмосферы уменьшает неблагоприятный эффект теплового расплывания
, является скорость течения v частиц газовой среды, через которую проникает луч (см. рис.2). Однако маленькая плотность высоких слоев атмосферы уменьшает неблагоприятный эффект теплового расплывания ![]() .
.
Заключение
В данной работе мы рассматривалась математическая модель передачи лазерной энергии стратосферному дирижаблю, характеризуемому подвешенным полетом и питаемому дистанционно из лазера космического базирования, установленного на геостационарной орбите с учетом необратимых потерь. Проект сокращенно получил название лазерного стратосферного многоцелевого дирижабля (ЛСМД).
В дальнейшем планируется рассмотреть задачу об эффективности передачи лазерного излучения с учетом необратимых потерь.
Литература
- Базухаир М. А. Концепция стратосферного многоцелевого дирижабля с лазерным питанием из лазера космического базирования.: Молодой ученый. — 2015. — № 82. С. 126-130.
- Average wind speed in the stratosphere is minimal at altitudes of about 20 km, [Электронный ресурс] URL: http://www.intercomms.net/AUG03/content/struzak 1.php (Дата обращения08.2014)
- Jacobson, Mark Z. Fundamentals of Atmospheric Modeling.: Cambridge University Press. – 2005. С. 317.
- Richard Mason, feasibility of laser power transmission to a high-altitude unmanned aerial vehicle / Technical report of RAND // prepared for the united states air force. – 2011. С. 73
- Solar Calculation Details / Earth System Research Laboratory // NOAA Solar Calculations day. [Электронный ресурс] URL: http://www.esrl.noaa.gov/gmd/grad/solcalc/calcdetails.html (Дата обращения 05.10.2014)
- Sprangle, J.R. Peñano, and A. Ting. Plasma Physics Division and B. Hafizi, Icarus Research, Inc., Propagation of High-Energy Lasers in a Maritime Atmosphere, U.S. Naval Research Lab 4555. [Электронный ресурс] URL: http://www.nrl.navy.mil/research/nrl-review/2004/featured-research/sprangle/ (Дата обращения 05.10.2014)
References
- Bazuhair M. A. Koncepcija stratosfernogo mnogocelevogo dirizhablja s lazernym pitaniem iz lazera kosmicheskogo bazirovanija.: Molodoj uchenyj. — 2015. — № 82. S. 126-130.
- Average wind speed in the stratosphere is minimal at altitudes of about 20 km, [Jelektronnyj resurs] URL: http://www.intercomms.net/AUG03/content/struzak 1.php (Data obrashhenija 20.08.2014)
- Jacobson, Mark Z. Fundamentals of Atmospheric Modeling.: Cambridge University Press. – 2005. S. 317.
- Richard Mason, feasibility of laser power transmission to a high-altitude unmanned aerial vehicle / Technical report of RAND // prepared for the united states air force. – 2011. S. 73
- Solar Calculation Details / Earth System Research Laboratory // NOAA Solar Calculations day. [Jelektronnyj resurs] URL: http://www.esrl.noaa.gov/gmd/grad/solcalc/calcdetails.html (Data obrashhenija 05.10.2014)
- P. Sprangle, J.R. Peñano, and A. Ting. Plasma Physics Division and B. Hafizi, Icarus Research, Inc., Propagation of High-Energy Lasers in a Maritime Atmosphere, U.S. Naval Research Lab 4555. [Jelektronnyj resurs] URL: http://www.nrl.navy.mil/research/nrl-review/2004/featured-research/sprangle/ (Data obrashhenija 05.10.2014)