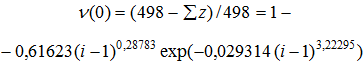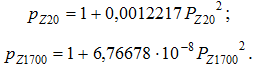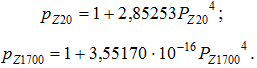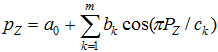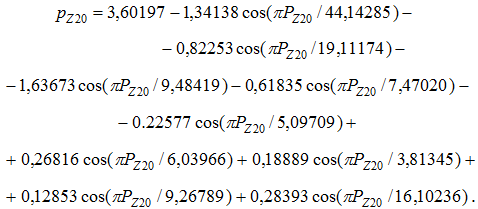ПРИРОСТ ЦЕЛЫХ ПРОСТЫХ ЧИСЕЛ

Мазуркин П.М.

Доктор технических наук, Поволжский государственный технологический университет

ПРИРОСТ ЦЕЛЫХ ПРОСТЫХ ЧИСЕЛ

Аннотация

Главным отличительным признаком прироста, как «ступенек» от «лестницы Римана», является вторая вертикаль квантификации. При квантификации простых чисел переводом их из десятичной в двоичную систему счисления только эта вертикаль заполняется полностью. Заполнение второй вертикали нетривиальными нулями и единицами наблюдается на ряде целых простых чисел любой мощности, до бесконечности. 

Ключевые слова: целые простые числа, прирост, критичная линия, корень 1/2, волновые закономерности

Mazurkin P.M.

Doctor of Technical Sciences, Volga State University of Technology

INCREMENT INTEGER PRIMES

Abstract

The main feature of the growth as "stu-stump" from the "ladder Rome" is the second vertical quantification. When quantification primes transfer them from decimal to binary number system only this vertical is filled completely. Fill-second of vertical non-trivial zeros and ones observed in the number of primes of any integer power indefinitely.

Keywords: integer prime number, increment, the critical line, the root of 1/2 wave patterns

Прирост простых чисел

Ряд простых чисел (ПЧ) можно представить как череду годичных приростов многолетнего растения (табл. 1), например, в высоту или толщину.

Такая аналогия с биологическими процессами наглядна [9]. В итоге прирост можно рассматривать обособленно от ряда простых чисел (ступеньки отделены от основания гауссовой лестницы). Лучше всего оказалось принятие зависимости прироста от самого простого числа. Причем оказалось, что анализ прироста нагляднее из-за компактности записи прироста ряда простых чисел в двоичной системе счисления.

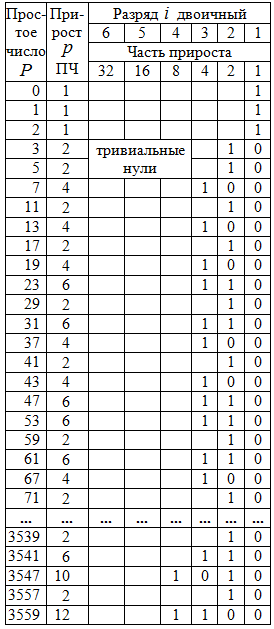
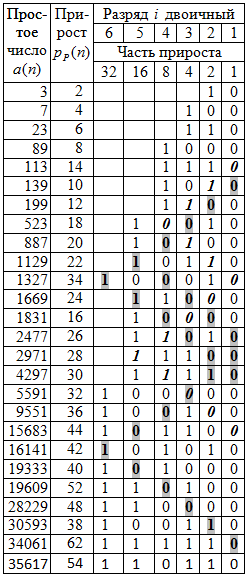
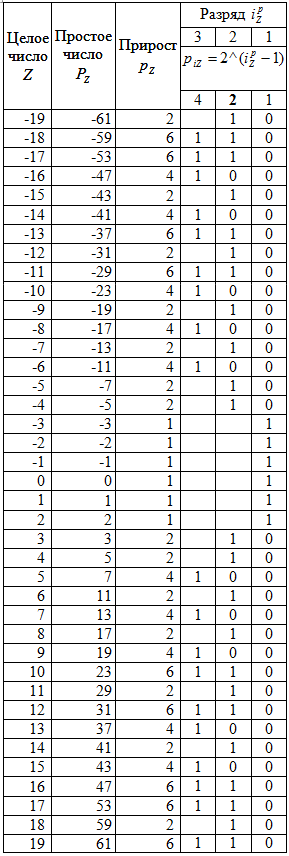
Таблица 1 - Ряд прироста 500 простых чисел в двоичной системе счисления

 

Коренное отличие ряда прироста от самого ряда простых чисел заключается в том, что в приросте (тоже число – абстрактная мера количества) только один столбец i=2 разряда двоичных чисел (или критической линии Римана) является полностью заполненным. А первый разряд имеет нетривиальные нули (кроме прироста 1 у критичных простых чисел 0, 1, 2) для множества P>2.

Полное заполнение второго столбца, начиная с простого числа 3,  продолжится до бесконечности, поэтому можно считать доказанным факт очередного появления минимального прироста p=2 при любой мощности P, вплоть до бесконечности. Отсюда следует, что столбец i=2 является критической линией, причем не только для рада приростов [6, 7], но критичной и для ряда простых чисел.

Математический ландшафт прироста

Все обращают внимание на нетривиальные нули и давно ищут их на критичной линии второй вертикали по данным таблицы 1. Их уже насчитали несколько триллионов [9]. Но до сих пор уверенности у математиков в их не тривиальности нет. Из таблицы 1 по приростам видно, на критичной линии Римана i=2, то есть на второй вертикали двоичного разложения прироста простых чисел, идет закономерное чередование нетривиального нуля и 1, в тривиальные нули начинают появляться уже с третьей вертикали. Доказательство того, что нетривиальные нули могут быть и не  на критичной линии Римана, видно также из таблицы 6: например, у простого числа 89 при приросте 8, впервые появляется нетривиальный нуль на третьей вертикали i=3.

Для построения математического ландшафта прироста (рис. 1) исключим из таблицы 1 те строки, в которых по пяти вертикалям находится хотя бы один тривиальный нуль. Это исходит из того, что пустые клетки (тривиальные нули в пустых клетках таблицы 1) не являются цифрами и поэтому программная среда CurveExpert-1.40 их не воспринимает.

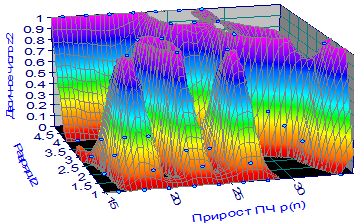
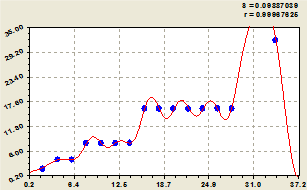
Рис. 1 - Ландшафт прироста в ряду из 500 простых чисел

Тогда минимальный, учтенный на рисунке 1, прирост среди 500 простых чисел был равен 16.

Показателем является двоичное число z=z₂ в области действительных чисел (0;1). Математический ландшафт прироста на рисунке 1 оказался сложнее ландшафта самих простых чисел.

Блоки двоичного разложения прироста имеют сложную линию по сравнению с  ступенчато расширяющейся влево границы блоков ряда простых чисел из 1 от второй вертикали или критичной линии Римана.

Влияние прироста на первом разряде

 Бернхард Риман в 1859 году по результатам анализа дзета-функции утверждал, что нетривиальные нули находятся на одной линии. После Харди доказал, что нетривиальные нули находятся и вне критичной линии. Ныне полагают, что она как критичная линия пересекает математический ландшафт дзета-функции. Пока наглядности через дзета-функцию так и не добились. Однако из данных таблицы 1 видно, что для нового параметра ряда – прироста простых чисел – такая единственная линия есть. Это – вертикаль j=2. Покажем, что остальные вертикали составляющих простых чисел всегда приближаются к критичной линии при условии j→∞.

Тем самым еще раз подтвердим доказательство Харди о том, что в ряду имеется бесконечное множество нетривиальных нулей, часть которых может и не лежать на критичной линии Римана (см. простое число 3547 при приросте 10 в таблице 1, где есть нетривиальный нуль вне критичной линии).

Для первого разряда i=1 (рис. 2) двоичного разложения по нетривиальным нулям на первой вертикали имеем:

- для гауссова ряда (начинающегося с цифры 2) из 500 простых чисел

- для полного ряда 500+1 простое число

где j - порядок-ранг простого числа из полного ряда.

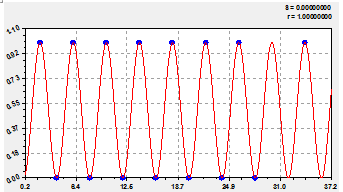
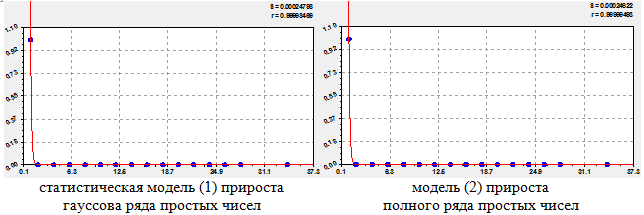 Рис. 2 - Графики распределения двоичного числа у прироста простых чисел на первом разряде двоичной системы разложения

Обе формулы являются законом экспоненциальной гибели (закон Лапласа в математике, закон Мандельброта в физике, закон Ципфа в биологии и закон Парето в эконометрике). Параметры закона экспоненциальной гибели изменились только из-за наличия впереди традиционного гауссова ряда цифр 0 и 1, то есть двоичной системы счисления.

Влияние прироста на двоичное число мало зависит от типа ряда простых чисел (ряд Гаусса, усеченный и полный ряд). Однако ясно, что при теоретическом нулевом приросте получаем огромное двоичное число 1781, намного превышающее 1. Этот факт указывает на аномальное влияние нулевого прироста на критических простых числах 0, 1 и 2.

Влияние прироста на втором разряде

На второй вертикали, как видно из данных таблицы 1, в обоих рядах прироста (гауссова ряда и полного ряда простых чисел) вначале находятся тривиальные нули (пустые клетки). Поэтому математическая обработка возможна только со строки P=3.

После статистического моделирования получаем фундаментальный закон прироста (рис. 3) для любого ряда простых чисел в виде уравнения

 

Рис. 3 - График распределения двоичного числа в зависимости от прироста 500+1 простых чисел по модели (3) на критичной линии Римана

Критичная линия Римана на вертикали i=2 получила однозначную формулу влияния прироста на двоичное число, причем с тригонометрической функцией косинуса без сдвига волны.

Математическая константа √2 по сравнению с самим рядом простых чисел исключилась.

В модели (3) остались три математические константы:

1) число 1;

2) 1/2 – рациональный корень по гипотезе Римана (этот корень 1/2 в формуле (6.3) встречается трижды);

3) π=3,14159… число Архимеда (число пространства).

Тогда получается, что из-за наличия π формула (3) показывает сущность свойств у пространства, причем без учета времени.

Влияние прироста на других разрядах

Для третьего разряда i=3 системы двоичного счисления исключим из вертикалей по таблице 1 клетки с тривиальными нулями. Тогда исключатся 97 первые числа у простых чисел-близнецов и останутся 402 строки.

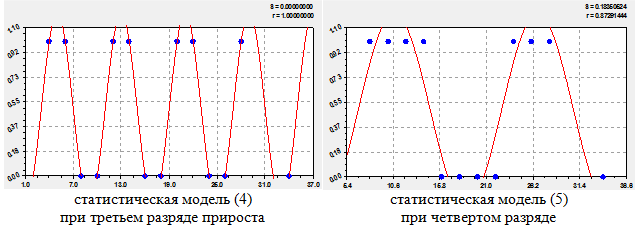
После идентификации (рис. 4) 402 значений получена закономерность

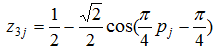
которая одинакова по конструкции с формулой (3), но не совпадает по сдвигу колебания (π/4 вместо π/2) параметру √2/2 перед функцией косинуса.

Для разряда i=4 (рис. 4) по 183 значениям оставшихся, после 500 членов ряда, простых чисел была получена формула

   

Рис. 4 - Графики распределения двоичного числа от влияния приростов простых чисел

Еще большее отклонение от критичной линии происходит на пятом разряде. Из 37 точек на пятой вертикали только одна получает 0, а остальные 36 приростов имеют значение 1.

Поэтому для повышения адекватности моделей на четвертом и последующих вертикалях нужно увеличивать мощность ряда простых чисел.

Влияние разряда двоичной системы счисления

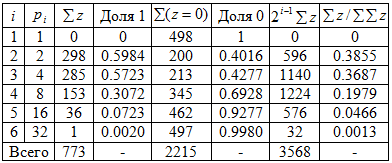
В среде Excel суммируем по столбцам таблицу 1 (с ) и получим количество единиц ∑z по разрядам двоичной системы счисления (табл. 2).

Таблица 2 - Влияние разряда двоичной системы (498 строк)

  

Модели лучше давать по относительным величинам - долям, что позволяет сравнивать разные по мощности ряды простых чисел.

После идентификации биотехнического закона [2-4] были поучены следующие статистические закономерности:

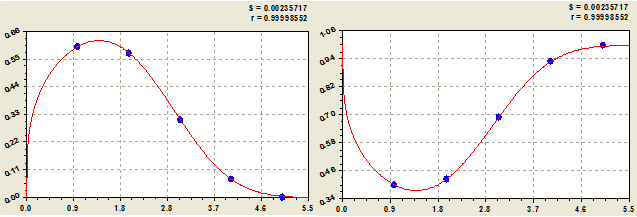
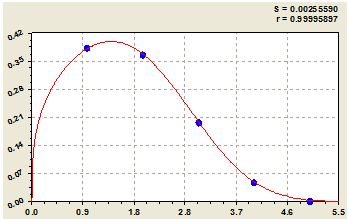
- доли 1 в (рис. 5) строках двоичной матрицы прироста простых чисел

- доли нулей (рис. 5), включая тривиальные и нетривиальные нули, в строках двоичной матрицы прироста простых чисел

 

Рис. 5 - Доля единиц (слева) и нулей (справа) в строках матрицы (табл. 2)

В пользу вычислений количества единиц вместо нулей имеются две отличительные особенности:

1. число нулей (тривиальных и нетривиальных) почти в три раза больше единиц (табл. 2);
2. по конструкции формула (6) биотехнического закона проще и компактнее по сравнению с математическим выражением (7).

По-видимому, параметр 0,61623 с ростом ряда  n→∞ будет приближаться к золотому сечению 0,618… . Получается, ориентировочно на критичной линии находятся φ^-1=0,618… единиц и 0,618² нетривиальных нулей.

Вклад суммы единиц по столбцам (рис. 6) к сумме (в таблице 2 эта сумма равна 773) будет равен

 

  Рис.  6. График вклада суммы единиц

На критической линии i=2 вклад суммы 1 приблизится к квадрату золотого сечения.по столбцам таблицы 6.2

По росту простого числа через формулу влияния m-числа Фибоначчи [10], мы косвенно получили функциональную связь с золотой пропорцией и другими математическим константами. При этом выяснилось, что число 1 - одно из основных понятий в теории групп - является фундаментальной математической константой.

Поэтому, деля 1 на 2,  получаем дробное число 1/2 – рациональный корень дзета-функции Римана [8].

А при рассмотрении отдельно ступенек лестницы Гаусса-Римана в формулах (6) и (7) мы четко получили, что на критической линии Римана (второй вертикали) приростов находятся φ^-1=0,618 единиц и 0,618² нетривиальных нулей. При условии  m=1 поучаем φ=Φ₁=(1+√5)/2 - золотая пропорция - или число 1,618… .

Начало координат четко определяется в точке (Z=0, P_z=0). Это – точка сингулярности из-за того, что по существующему определению простого числа (свойство деления на самого себя) происходит деление простого числа на самого себя, то есть 0 / 0.

При этом деление только на 1 превращает эту точку в нуль.

Минимальная выборка простых чисел

Методом отсечения снизу от строк таблицы 1 для ряда некритичных простых чисел определим минимальную выборку (табл. 3), где еще действует устойчивый закон критичной линии по формуле (3).

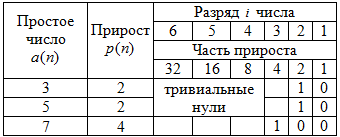
Таблица 3 - Минимальный ряд простых чисел в гауссовом ряду ПЧ

 

Минимальный ряд некритичных простых чисел образуют всего три члена, по которым было получено уравнение (3) с рациональными параметрами, приведенными в таблице 4. Погрешность приближения 0.5→1/2 пренебрежимо мала.

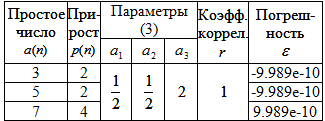
Таблица 4 - Влияние прироста ПЧ на двоичное число на втором разряде двоичной системы

 

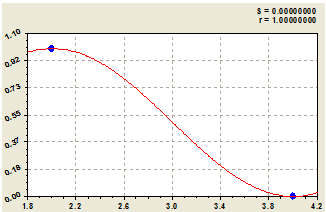
График простого по конструкции уравнения (3) с параметрами модели из таблицы 4 показан на рисунке 7.

Рис. 7 - График формулы (3) для трех не критических простых чисел

У других разрядов i₂>2 нужно возрастающее количество (мощность) простых чисел. Такое требование возникает из-за усложнения формулы (3) дополнительными параметрами модели.

Между приростом и его составляющей существует закономерность перехода чисел из десятичной системы счисления в двоичную. При этом прирост простых чисел оказывается более точным в сравнении с рядом ПЧ.

Реперы блоков простых чисел

Первые левые единицы образуют асимптотическую линию, левее которой находятся только тривиальные нули. При этом эта линия становится ломанной и ступенчато расширяющейся с ростом разряда двоичной системы счисления.  Рассмотрим реперы в ряде из 500 простых чисел.

Репера образуют блоки и тем самым становятся новым параметром, характеризующим распределение простых чисел. В массиве из 500 точек прироста ПЧ их немного (табл. 5), всего пять.

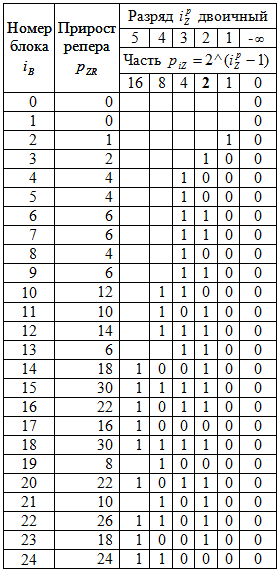
Таблица 5 - Репера прироста 500 ПЧ

 

Исходя из условия, что в начале ряда (см. табл. 1) прирост равен единице, была получена (рис. 8) формула

где индекс R обозначает реперное простое число или число на границе блока.

Рис. 8 - График реперной функции прироста

Применение реперов гораздо компактнее известного отношения x/π(x).

Как было показано в статье [5], посвященной блочной структуре ряда целых простых чисел (ЦПЧ), репера блоков позволяют «заглянуть» далеко вперед относительно заранее известной линии 2^i-1

Первичный прирост

Это – третий показатель (первый – критичная линия, второй – репера блоков), дающий картину роста прироста  простых чисел.

Первичный прирост показывает последовательность прироста по росту значений с учетом его положения в ряду прироста простых чисел.

Параметр первичного прироста p_p(n) для ряда из 100 000 простых чисел приведен в таблице 6. Первичный прирост нерегулярен, например, прирост 14 появляется после 8 и раньше значений 10 и 12. на это сильно влияет геометрия распределения простых чисел и их приростов. Различным шрифтом выделены треугольники (узоры геометрии) со сторонами (при i₂₌₁ – нетривиальные нули). Тогда гармоничные геометрические структуры определяют алгоритм наращивания прироста и даже простого числа.

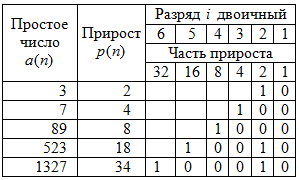
Таблица 6 - Первичный прирост в ряду из 100 000 членов

    Тогда гармонично расположенные относительно ряда ПЧ геометрические структуры определяют неизвестный пока алгоритм наращивания (генерации) прироста и даже самого простого числа.

Например, в данных таблицы 6 четко видны два треугольника с вершиной на приросте 34 у простого числа 1327 в виде общей фигуры

Рис. 9 - Фигура треугольника с вершиной 34

Основание треугольников выполнено из вертикального ряда нетривиальных нулей из первого разряда двоичной системы счисления.

А боковые линии должны быть симметричными по диагональному ряду из одного набора 0 и 1. тогда получается, что прирост 34 появляется в ряду ПЧ только из-за того, чтобы построить красивую фигуру.

Линия первичного прироста меняется с начальной постоянной «двойкой», а дальше будут колебания, по тренду

Для условия n→∞ всегда будет p_min(n)=2.

Огибающая линия ряда прироста

Приросты левее асимптотической линии имеют тривиальные нули. Поэтому учитывается волновая огибающая линия, которая в разных местах касается критичной линии i₂=2. Это –  четвертый параметр ряда прироста.

Разделим прирост на две части p(n)=p′(n)+p″(n). На огибающей линии построчно в таблице 1 (рис. 10) находятся части прироста p′(n)=2ⁱ_2max^-1.

Рис. 10 - График огибающей линии прироста ряда из 500 простых чисел

А внутри располагаются части прироста 0≤p″(n)= 2ⁱ_2max^-1.

Тренд с единицей из формулы с тремя колебаниями имеет вид

При условии n→∞ в формуле (11) всегда будет 1 в начале ряда простых чисел.

Частные огибающие линии можно построить по характерным переходам между строками прироста по ходу возрастания ряда простых чисел.

Особенности прироста целых простых чисел

Этот новый показатель оказался наглядным и в то же время математически более простым для изучения ряда простых чисел.

Прирост изменяется по тем же разрядам системы двоичного счисления, поэтому i=i_j^P=i_j^p. Для примера примем ряд ЦПЧ с правой границей блоков P_Z″=61 из таблицы 3 и оставим только двоичное разложение приростов (табл. 7).

Вторая вертикаль двоичного разложения прироста ЦПЧ по данным таблицы 7 получает два отличительных признака:

• центр симметрии на второй вертикали имеет тривиальные нули, поэтому прирост ряда ЦПЧ имеет центральный разрыв, который позволяет отдельно рассматривать отрицательную и положительную ветви прироста;
• при этом приросты по обоим направлениям (отрицательному и положительному) вдоль оси абсцисс положительные, что дает возможность анализа только одной правой части в виде полуоси положительных натуральных чисел, начиная с 3;
• положительные приросты дает возможность анализа по всей оси целых чисел, так как обе ветви приростов симметрично изменяются относительно отрицательной и положительной сторон шкалы целых чисел.

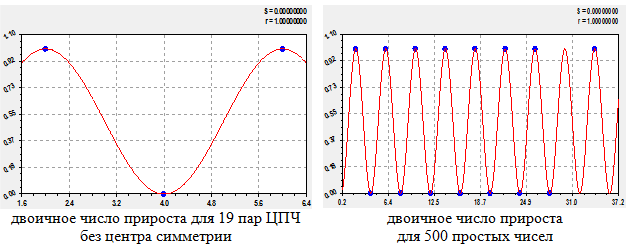
Двоичное число на второй вертикали (рис. 11) определяется при любой мощности ряда ЦПЧ формулой вида

Рис. 11 - Графики двоичного числа по второй вертикали разложения ЦПЧ

Таблица 7 - Прирост ЦПЧ

 

В  итоге повторяется формула (3) и фундаментальный закон прироста (рис. 11) действителен для любого ряда в виде ПЧ или ЦПЧ. При этом в законе (12) повторяется три раза действительный корень 1/2.

Бесконечность ряда простых чисел была доказана 2300 лет назад Евклидом. Поэтому ряд прироста простых чисел также является бесконечным.

Тогда становится очевидным, что количество реперов и часть от них в виде простых чисел-близнецов Голстона также обладает свойством стремиться к бесконечности.

Если есть ряды с постоянным приростом 2, то должны быть и ряды с постоянными другими четными числами 4, 6, 8, … . Поэтому мы предложили новый класс рядов ПЧ и ЦПЧ – это простые числа с постоянным приростом.

Скачки прироста по блокам

В таблице 8 показано разложение прироста реперов (скачков между блоками) в ряду из 10 млн. простых чисел. Тривиальные нули не учитываются.

Тогда, начиная с прироста 2 (рис. 11), снова соблюдается формула (12).

Таким образом, прирост ПЧ и ЦПЧ одинаков для разной длины рядов, не зависит от блоков и это упрощает анализ и специальных рядов простых чисел.

Таблица 8 - Прирост реперов блоков

Для проверки достоверности возможна простая рекомендация: если приросты чисел в специальном ряду не удовлетворяют условию формулы (12), то этот ряд или очередное сгенерированное число не относится к простым числам.

Прирост на двоичное число

За объясняющую переменную берем прирост простого числа.

Тогда по разным разрядам двоичной системы счисления образуются свои статистические модели типа

где a₁…a₆ - параметры модели (13).

Если не учитывать первый и последний разряды двоичной системы, то близко к рациональному числу 1/2 по вещественным значениям находится разряд i₂=2 (критичная линия Римана).

Для критической линии i₂=2  формула (13) редуцируется (рис. 12) к упрощенному, без сдвига волны и при постоянной частоте 1/2,  виду

Но расчетное значение двоичного числа (поэтому специалисты по шифрованию могут не беспокоиться) всегда будет иррациональным только из-за того, что в формуле содержится иррациональное число Архимеда (число пространства) π «пи» с разной точностью записи.

Формулу (12) можно проверить на любом ряде простых чисел.

На рисунке 12 показан график прироста на втором столбце (разряде двоичного числа) для ряда А000040.

Рис. 12 - Графики формулы (12) для ряда простых чисел А000040

Гипотеза Римана полностью доказана и вторым столбцом двоичной записи прироста простых чисел снимаем следующее сообщение для математиков из Интернет: «А вот знаменитая гипотеза Римана, что вещественная часть корня всегда в точности равна 1/2, ещё никем не доказана, хотя её доказательство имело бы для теории простых чисел в высшей степени важное значение. В настоящее время гипотеза проверена для 7 миллионов корней».

С увеличением мощности простых чисел уравнение (12) для критической линии сохранится, только на графиках типа рисунков 13 будут частые колебания из-за повышения прироста с ростом номера простого числа.

Но прирост нарастает гораздо медленнее простого числа. И эта особенность ряда прироста дает практическую возможность наглядного анализа.

Проверка закона критичной линии

Проверим устойчивость уравнения закона критической линии Римана  на других примерах. Докажем, что на критической линии i₂=2 указанная модель (12) распределения прироста устойчива и при других количествах (другой мощности) в ряду простых чисел.

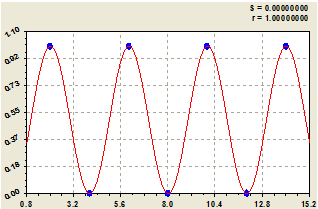
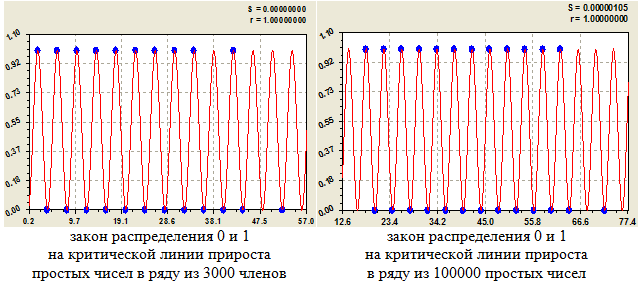
На рисунке 13 показаны графики распределения по формуле закона критической линии (12) прироста для рядов из 3000 и 100000 простых чисел.

Максимальный прирост 52 получает двоичное число, равное нулю. При этом единица находится только на приросте 42. С дальнейшим ростом численности ряда простых чисел волна по функции косинуса будет продолжаться и дальше. Это видно также из графика на рисунке 13 по распределению двоичного числа по формуле  на критической линии Римана по вертикали i₂=2 для 100000 простых чисел.

Рис. 13 - Графики формулы (6.12) для доказательства гипотезы Римана

Распределение прироста гораздо компактнее ряда простых чисел.

С увеличением мощности ряда до 3000 по сравнению с массивом 500 (рис. 11) возрастает количество точек прироста в графике (рис. 13). Но при этом программная среда CurveExpert включает в график по оси абсцисс весь интервал изменения прироста от 2 до 52. Для проверки было взято только подмножество (1704 строки) приростов p(n)≥18 из 100 000 простых чисел. Максимальное значение прироста равно 72 с нулем двоичного числа.

С увеличением численности приростов, из-за роста максимального прироста, график двоичного числа становится недостаточно наглядным.

Отсюда следует, что в любой выборке приростов простых чисел разной численности соблюдается закон  критической линии Римана. Мы вручную проверили ряд простых чисел до 100000. Но эффективнее составить программу для составления ряда прироста по формуле (12), а затем проверять закон  на больших рядах.

Проверка правильности простых чисел выполняется легко:

если нарушается график прироста по закону

то члены такого ряда неверны, то есть найденное число не является простым. Это будет критерием проверки простоты генерируемого простого числа.

Простые числа как шкала для прироста

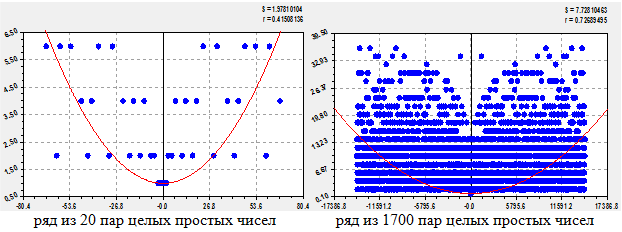
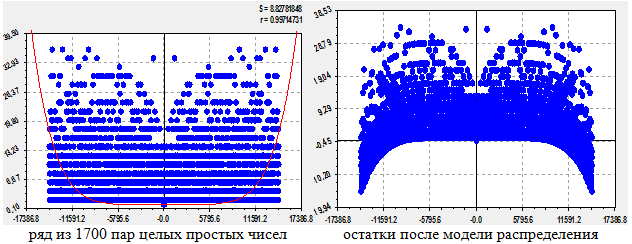
Далее для сравнения рассмотрим примеры прироста у двух симметричных рядов ЦПЧ с количеством пар простых чисел 20 и 1700 (близко к пределу заполнения исходными данными программной среды CurveExpert-1.40).

Отрицательные числа придется возводить в квадрат или иную чётную степень, то есть применять уравнения с натуральными четными числами.

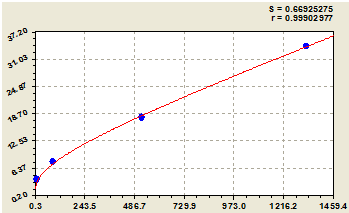
По двум симметричным конечномерным рядам (рис. 14) были получены уравнения со степенями 2:

  

С увеличением количества пар ЦПЧ коэффициент корреляции квадратичной формулы изменения прироста в зависимости от значений самих простых чисел возрастает.

Рис. 14 - Квадратичная зависимость прироста от целых простых чисел при различных количествах пар ЦПЧ

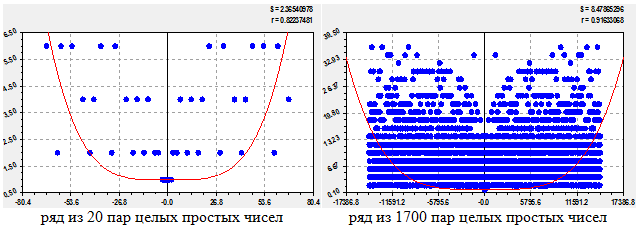
Построим эту закономерность и на других степенях (рис. 15):

Рис. 15 - Четвертичная зависимость прироста от целых простых чисел при различных количествах пар ЦПЧ

Адекватность формул (16) и (17) значительно повысилась.

Тогда получается, что Гаусс не совсем был прав, принимая для аппроксимации симметричных (нормальных) распределений квадратичную форму.

Четвертая степень распределения куда интереснее. Шестая степень у численности из 20 пар не получается, а восьмая степень дает коэффициент корреляции более 1 (то есть неверная статистическая закономерность).

Поэтому для достаточно мощных по численности членов симметричных рядов ЦПЧ подходит (рис. 16) статистическая модель

Поэтому может оказаться, что четная степень будет нарастать с ростом мощности ряда целых простых чисел.

Рис. 16 - Шестеричная зависимость прироста от целых простых чисел при количестве 1700 пар целых простых чисел

Однако такую гипотезу можно будет проверить только на суперкомпьютере со специальной программной средой, позволяющей рассматривать и другие варианты закономерностей, кроме формулы (18).

Число 6 в степени формулы (18) символичное, его можно интерпретировать как два векторных направления (+ и -) по трем осям пространства [1].

Волновая структура прироста по рядам ЦПЧ

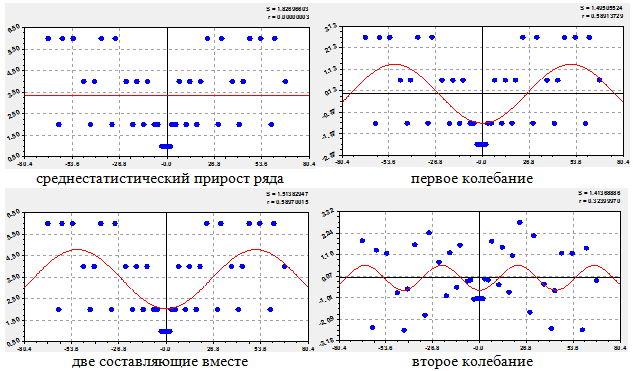
Для наглядности берем только 20 пар целых простых чисел. Последовательность регулярных волн приведена на рисунках 17 и 18.

Рис. 17 - Последовательность идентификации первых гармоник прироста 20 пар ЦПЧ

Индуктивно можем записать общую формулу множества гармоник

 

Если бы удалось выявить однозначную статистическую модель, то она стала бы генератором ряда целых простых чисел.

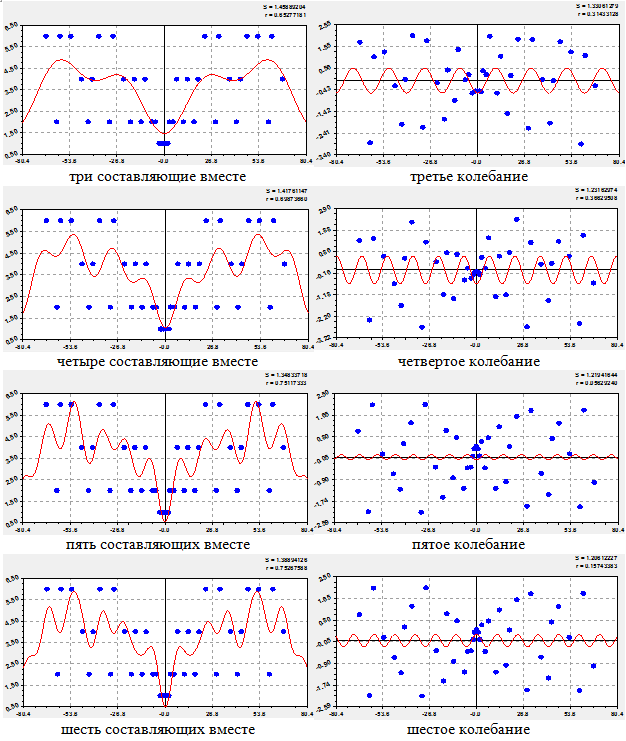
Новыми составляющими в виде колебаний график общей волновой функции усложняется (рис. 18).

Пока можем сказать, что прирост равен бесконечной сумме гармоник.

Рис. 18 - Продолжение последовательности гармоник прироста в ряду из 20 пар ЦПЧ

Предыдущие пять колебаний были с отрицательным знаком (кризисная волновая адаптация), а шестое колебание по рисунку 6.19 и последующие гармоники стали положительными.

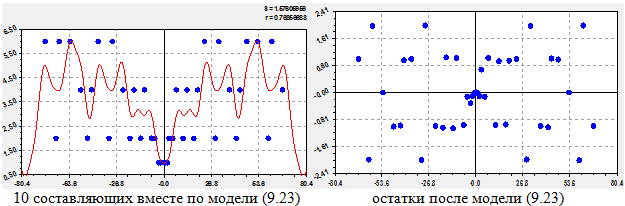
На рисунке 19 показан график после 10 составляющих (предел программной среды CurveExpert-1.40 с 19 параметрами модели) по уравнению

Рис. 19 - График функции из девяти гармоник прироста в ряду из 20 пар ЦПЧ

Из остатков на рисунке 19 видно, что ядро центра симметрии как бы стягивает с двух сторон по шкале целых чисел значения приростов у всего ряда некритичных простых чисел. При этом стягивание по полуосям или рукавам происходит асимметрично, но постепенно всё возрастающее количество точек прироста сжимается по амплитуде колебаний вокруг центра симметрии всего конечномерного ряда целых простых чисел.

Выводы

На основе статистического моделирования рядов целых простых чисел получили фундаментальный закон прироста на критичной линии Римана в виде уравнения

где z₂^p - двоичное число, вещественно изменяющееся от 0 до 1 на второй вертикали матрицы двоичного разложения целых простых чисел,

p_z - прирост целого простого числа, представляемого физически как ступеньки лестницы Гаусса-Римана, располагающиеся вдоль оси ЦПЧ

z- ось абсцисс целых чисел, ранг ЦПЧ от -∞ до +∞,

1/2 - действительный корень дзета-функции Римана, встречающийся три раза в этой формуле.

Вычислительные эксперименты показали, что трудоемкость моделирования простых чисел ускоренно возрастает с увеличением численности членов ряда. Наилучшим факторным отношением становится влияние простого числа на свой прирост. Прирост нарастает гораздо медленнее самого простого числа. И эта особенность ряда прироста дает практическую возможность наглядного анализа до 100000 простых чисел и более.

Нетривиальные нули имеются и в других разрядах двоичной системы счисления прироста простых чисел, причем вдоль ряда простых чисел они расположены вперемежку с тривиальными нулями.

Первые граничные единицы образуют асимптотическую ломаную линию, левее которой находятся только тривиальные нули. Репера образуют в матрице двоичного представления прироста отдельные блоки. Даже в массиве из 100 000 простых чисел их немного, всего пять. На ступенчатой матрице двоичного представления прироста репер располагается в левом верхнем углу каждого блока. Применение реперов гораздо компактнее известного математикам отношения x/π(x).

Первичный прирост – третий показатель (первый – критическая линия ½, второй - репера), дающий картину роста прироста у ряда простых чисел. Он показывает последовательность прироста по росту значений с учетом его положения в ряду прироста простых чисел. Причем первичный прирост, по нарастающим простым числам, расположен нерегулярно, например, первичный прирост 14 появляется после 8 и раньше значений 10 и 12.

Приросты правее асимптотической линии имеют нетривиальные нули. Поэтому учитывается волновая огибающая линия, которая в разных местах касается критичной линии i₂=2. Это –  четвертый параметр ряда прироста простых чисел. Огибающая имеет вид ступенчатой линии.

Критичная линия Римана на второй вертикали матрицы двоичного счисления прироста была проверена на рядах из 500, 3000 и 100000 простых чисел. В любой выборке приростов простых чисел разной численности соблюдается закон критической линии Римана.

В формуле критичной линии содержится иррациональное число π=3,14159…, то есть фундаментальная физическая постоянная пространства (число Архимеда). Закон критичной линии не угрожает криптографии.

Литература

1. Герштейн С.С., Логунов А.А., Мествиришвили М.А. Гравитационные волны в релятивисткой теории гравитации // Теоретическая и математическая физика, 2009, 160: 2, 270-275. URL: tmf6397.pdf.
2. Мазуркин П.М. Биотехнический закон и конструирование адекватных моделей // Успехи современного естествознания. 2009. № 9. С.125-129.
3. Мазуркин П.М. Биотехнический закон, эвроритм и алгоритм поиска параметров // Успехи современного естествознания. 009. № 9. С.88-92.
4. Мазуркин П.М. Биотехнический принцип в статистическом моделировании // Успехи современного естествознания. 2009. № 9. С.107-111.
5. Мазуркин П.М. Блоки целых простых чисел // Х Международная научно-практическая конференция «Научное обозрение физико-математических и технических наук в XXI веке». Ежемесячный научный журнал «Prospero». №5. 2014. С. 23-34.
6. Мазуркин П.М. Прирост простых чисел // Современные наукоемкие технологии. 2012. № 10. С.31-39.
7. Мазуркин П.М. Прирост у целых простых чисел // Сборник научных трудов SWorld. Выпуск 3. Том 4. Одесса: КУПРИЕНКО СВ, 2013. ЦИТ: 313-0468. С.43-48.
8. Цагир Д. Первые 50 миллионов простых чисел. URL: http://www.egamath.narod.ru/ Liv/Zagier.htm.
9. Mazurkin P.M., “Wavelet Analysis of a Number of Prime Numbers.” American Journal of Numerical Analysis, vol. 2, no. 2 (2014): 29-34. doi: 10.12691/ajna-2-2-1.
10. 1 Vera W. de Spinadel. From the Golden Mean to Chaos. Nueva Libreria, 1998 (second edition, Nobuko, 2004).

References

1. GersteinS.S, LogunovA.A, Mestvirishvili M.A.Gravitational waves in therelativistictheory of gravitation//Theoretical and Mathematical Physics, 2009, 160: 2, 270-275. URL: tmf6397.pdf.
2. MazurkinP.M.Biotechnicallawand constructionof adequate models//Successes contemporary science. 2009. № 9. Р.125-129.
3. MazurkinP.M.Biotechnicallawevroritmandsearch algorithmparameters//Successes contemporary science. 2009. № 9. Р.88-92.
4. MazurkinP.M.Biotechnicalprinciple instatistical modeling//Successes contemporary science. 2009. № 9. Р.107-111.
5. MazurkinP.M.integerblocksof prime numbers//X-International onscientific andpractical conference"Scientific Reviewof physical and mathematicalsciences and engineeringin the XXI century." Monthlyscientific journal«Prospero».№5.2014. Р.23-34.
6. MazurkinP.M.Gainprimes//Modern high technologies. 2012. № 10. Р.31-39.
7. MazurkinP.M.Growthin wholeprimes//Collection of scientific worksSWorld.Issue 3.Volume 4.Odessa:KuprienkoNE,2013.CIT: 313-0468. Р.43-48.
8. D.Zagier. First 50 millionprimes.URL: http://www.egamath.narod.ru/ Liv / Zagier.htm.
9. Mazurkin P.M., “Wavelet Analysis of a Number of Prime Numbers.” American Journal of Numerical Analysis, vol. 2, no. 2 (2014): 29-34. doi: 10.12691/ajna-2-2-1.
10. 1 Vera W. de Spinadel. From the Golden Mean to Chaos. Nueva Libreria, 1998 (second edition, Nobuko, 2004).