О НЕКОТОРЫХ СВОЙСТВАХ БАЗЫ НЕЧЕТКИХ ПРОДУКЦИОННЫХ ПРАВИЛ
Сергиенко М.А.
Кандидат технических наук,
Воронежский государственный университет
О НЕКОТОРЫХ СВОЙСТВАХ БАЗЫ НЕЧЕТКИХ ПРОДУКЦИОННЫХ ПРАВИЛ
Аннотация
В статье представлены свойства базы нечетких продукционных правил и критерии их проверки.
Ключевые слова: продукция, база нечетких продукционных правил.
Sergienko M.A.
PhD in Technical Sciences,
Voronezh State University
ABOUT SOME PROPERTIES OF FUZZY RULES BASE
Abstract
The article considers the properties of fuzzy rules base and the criteria for their verification.
Keywords: production, fuzzy rule base.
Рассмотрим базу нечетких «если-то» правил 
вида
где 
– входные переменные, которые могут быть как четкими, так и нечеткими; 
– область определения входной переменной (посылки), 
– область определения соответствующей переменной, 
– область определения выходной переменной (заключения); 
– нечеткие множества, определенные на 
с функциями принадлежности 
соответственно [1].
Пусть 
– нечеткое множество, определенное на X, с функцией принадлежности 
, тогда 
примет вид
.
Рассмотрим некоторые свойства базы нечетких продукционных правил и критерии их выполнения.
Частичная непротиворечивость
Два правила, имеющие одинаковые условия, 
и являются несовместными по заключениям со степенью α , если
,
где T, I – Т-норма и оператор импликации соответственно [1].
База правил 
называется частично непротиворечивой (совместной), если она не содержит несовместные по заключениям правила.
Правило 
совместно с базой , если из непротиворечивости следует, что база 
также непротиворечива.
Полнота
Понятие полноты базы нечетких продукционных правил можно рассматривать как в узком, так и широком смыслах.
База правил полна в узком смысле, если не существует такого правила R, которое совместно с этой базой.
Определение полноты базы правил в широком смысле предлагается трактовать через понятия численной и лингвистической полноты.
Нечеткая модель является полной, если с каждым входным состоянием 
, принадлежащим области X, она может связать некоторое выходное состояние 
[2].
Нечеткая модель является неполной, если с некоторым входным состоянием 
нельзя связать ни одного выходного состояния 
.
Нечеткое разбиение области значений 
переменной 
является полным, если выполнено следующее соотношение
,
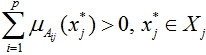где p – число нечетких множеств 
, которые могут быть значениями .
Полная нечеткая модель представляет собой более точную модель реальной системы, чем неполные.
Пусть в нечеткой модели с каждым входом ассоциирована лингвистическая шкала 
, пространство входных лингвистических значений задается 
, которое определяет все возможные лингвистические состояния входного вектора 
, а выход задан лингвистической шкалой 
.
База правил называется лингвистически полной, если каждому входному лингвистическому состоянию она ставит в соответствие хотя бы одно выходное лингвистическое состояние 
.
Численно полной называется база правил, для которой каждое четкое входное состояние 
приводит к активизации хотя бы одного правила (т.е. его заключения).
Поскольку активизация «хотя бы одного правила» позволяет вычислить значение на выходе модели, это определение, по своей сути, соответствует определению полной нечеткой модели.
Заметим, что лингвистически неполная база правил может быть численно полной, если подобраны функции принадлежности с достаточно широкими носителями. Если нечеткое разбиение областей значений входных параметров является неполным, то даже лингвистически полная база правил может не являться полной численно.
Частичная избыточность
Два правила 
являются специфичными по условиям/заключениям со степенью α, если 
В частности, если база правил содержит правила 
такие, что 
, то правило 
более специфично по условию, чем 
.
Два правила идентичны по условиям/заключениям со степенью α, если
где T – Т-норма, I – оператор импликации.
База правил называется частично избыточной, если в ней содержатся правила, идентичные по посылкам или заключениям.
Разделимость
База правил называется разделимой, если 
где 
– ядро нечеткого множества 
– носитель нечеткого множества 
.
Из данного определения следует, что удаление какого-либо правила из базы приводит к появлению таких значений входных переменных, к которым не применимы оставшиеся правила.
Литература
- Леденева Т.М. Обработка нечеткой информации: учебное пособие. – Воронеж: Воронежский государственный университет, 2006. – 233 с.
- Пегат А. Нечеткое моделирование и управление. – М.: БИНОМ, 2009. – 798 с.
References
- Ledeneva T.M. Obrabotka nechetkoj informacii: uchebnoe posobie. – Voronezh: Voronezhskij gosudarstvennyj universitet, 2006. – 233 s.
- Pegat A. Nechetkoe modelirovanie i upravlenie. – M.: BINOM, 2009. – 798 s.