АНАЛИТИЧЕСКОЕ РЕШЕНИЕ НЕЛИНЕЙНОГО УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО МАЯТНИКА
Сарбасов Е.К.1, Шагатаева З.Е.2
1Кандидат технических наук,
2Магистр образования,
Жетысуский государственный университет им. И.Жаснсугурова, Республика Казахстан
АНАЛИТИЧЕСКОЕ РЕШЕНИЕ НЕЛИНЕЙНОГО УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО МАЯТНИКА
Аннотация
В работе получено аналитическое решение задачи о нелинейном колебании эллиптического маятника методом частичной дискретизации нелинейных уравнений. Полученное решение сравнивается с решением задачи, соответствующего малым колебаниям, описывающейся системой линейных уравнений.
Ключевые слова: маятник, нелинейные уравнения, колебания.
Sarbasov Y.K.1, Shagatayeva Z.E.2
1Candidate of Technical Sciences,
2Master of education,
Zhetysu State University named after I. Zhansugurov, Republic of Kazakhstan
ANALYTICAL SOLUTION OF THE NONLINEAR EQUATION OF THE ELLIPTIC PENDULUM
Abstract
In work the analytical solution of a task on nonlinear fluctuation of an elliptic pendulum is received by method of partial sampling of the nonlinear equations. The received decision is compared to the solution of a task, corresponding to small fluctuations, the described system of the linear equations.
Keywords: pendulum, nonlinear equations, fluctuations.
Система имеет две степени свободы. В качестве независимых координат возьмем абцисы х центра тяжести тела М1 и угол отклонения стержня от вертикали. Изучим закономерность нелинейного отклонения тела М2, принимаемого за материальную точку.
Нелинейное уравнение движения эллиптического маятника имеет вид
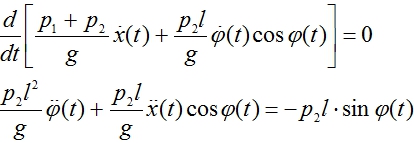 (1)
(1)
Ниже решим следующую задачу
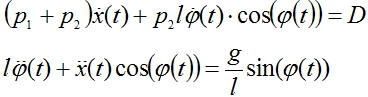 (2)
(2)
Для малых углов отклонения φ справедливы следующие уравнения
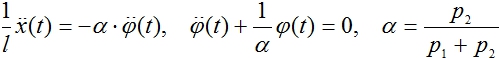
Начальные условия
![]()
Из уравнений (2) имеем
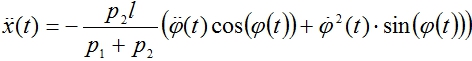 (3)
(3)
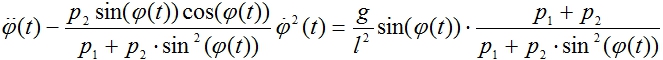 (4)
(4)
Частичная дискретизация [1-4] в классе обобщенных функций дает
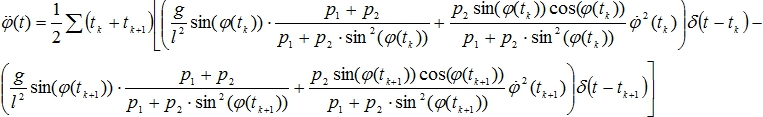 (5)
(5)
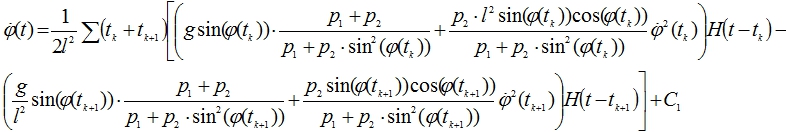 (6)
(6)
Общее решение (5) будет иметь вид
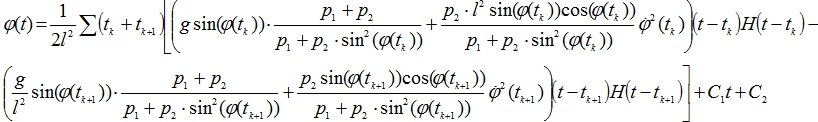 (7)
(7)
Таким образом решение задачи (1), (3) представляется в виде
![]() (9)
(9)
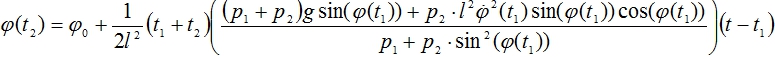 (10)
(10)
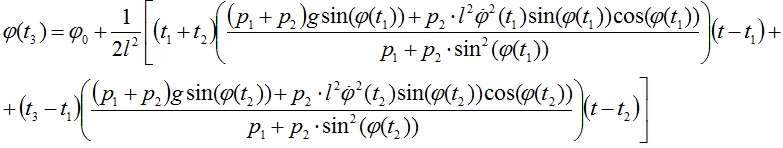 (11)
(11)
Используя метод математической индукции получая
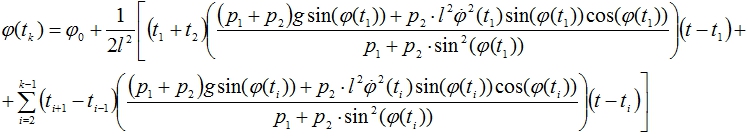 (12)
(12)
где
![]() (13)
(13)
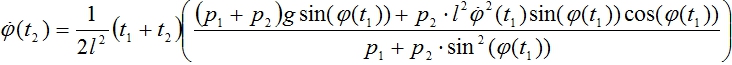 (14)
(14)
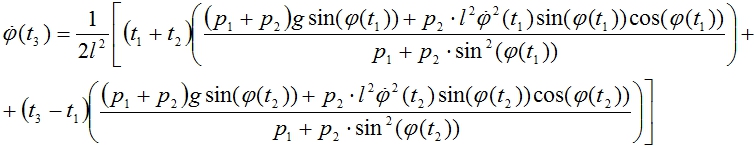 (15)
(15)
Методом математической индукции запишем выражение для
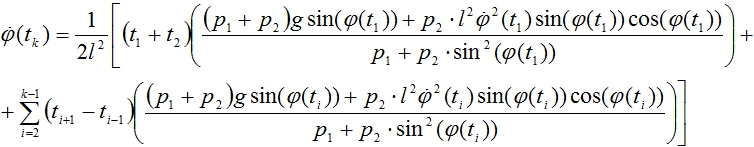 (16)
(16)
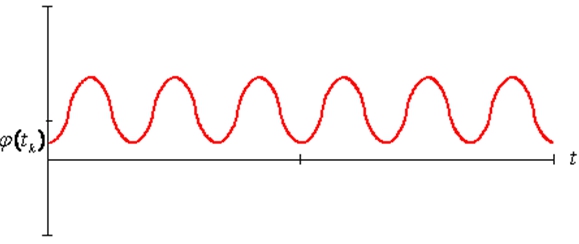
Рис. 1 - Колебание эллиптического маятника
Анализ полученного решения показывает, что система совершает установившееся колебание.
Литература
- Тюреходжаев А.Н., Шагатаева З.Е. Квазистатический гистерезис одномерной разномодульной системы с контактным сухим трением. Международный конгресс «Механика и трибология транспортных систем 2003». Ростов-на-Дону.
- Тюреходжаев А.Н., Шагатаева З.Е. О свободном колебании нелинейной разномодульной системы с контактным сухим трением. Вестник КазНТУ №1. Алматы. 2004.
- Тюреходжаев А.Н., Султаналиева Р.М., Шагатаева З.Е. Резонансное колебание разномодульной системы с контактным сухим трением. Международный научно-технический юбилейный симпозиум «Образование через науку», посвященный 50-летию ФПИ-КТУ им. И.Раззакова. Бишкек, 2004.
- А.Н.Тюреходжаев, А.Г.Ибраев, М.Ж.Сергазиев, Шагатаева З.Е. Распространение волн в механических системах с нелинейным механизмом диссипации энергии. Международная конференция «Дифференциальные уравнения, теория функции и приложения», посвященная 100-летию со дня рождения академика И.Н.Векуа Новосибирск, 2007г.
References
- Tyurekhodzhayev A.N., Shagatayeva Z.Y. Kvazistatic hysteresis of one-dimensional differently the modular system with contact dry friction. International congress "Mechanics and tribology of transport systems 2003". Rostov-on-Don.
- Tyurekhodzhayev A.N., Shagatayeva Z.Y. About free fluctuation of nonlinear differently the modular system with contact dry friction. Messenger of KAZNTU No. 1. Almaty. 2004.
- Tyurekhodzhayev A.N., Sultanaliyeva R. M., Shagatayev Z.Y. Resonant fluctuation of differently the modular system with contact dry friction. The international scientific and technical anniversary symposium "Education through science", FPI-KTU devoted to the 50 anniversary of I. Razzakov. Bishkek, 2004.
- A. N. Tyurekhodzhayev, A. G. Ibrayev, M. Zh. Sergaziyev, Shagatayeva Z.Y. Distribution of waves in mechanical systems with the nonlinear mechanism of dissipation of energy. The international conference "Differential Equations, Theory of Function and Appendix" devoted to the 100 anniversary since the birth of the academician I. N. Vekua Novosibirsk, 2007.
