ТОЧНОЕ АНАЛИТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ О ВЗАИМОДЕЙСТВИИ АТОМОВ ОБЛАДАЮЩИХ СФЕРИЧЕСКОЙ СИММЕТРИЕЙ ЭЛЕКТРОННЫХ ОБОЛОЧЕК

Баранов М.А.

Профессор, доктор физико-математических наук, Алтайский государственный технический университет

ТОЧНОЕ АНАЛИТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ О ВЗАИМОДЕЙСТВИИ АТОМОВ ОБЛАДАЮЩИХ СФЕРИЧЕСКОЙ СИММЕТРИЕЙ ЭЛЕКТРОННЫХ ОБОЛОЧЕК

Аннотация

Баланс зарядов разных знаков в атомах делает неправомерным применение приближённых и численных методов к определению энергии их кулоновского взаимодействия. Точные аналитические выражения этой энергии приводятся для атомов, электронные оболочки которых описываются произвольными функциями радиального распределения электронной плотности. Рассмотрены квантовые поправки. Данные выражения открывают возможность установления непосредственных связей между показателями свойств веществ и параметрами функций радиального распределения электронной плотности в оболочках атомов.

Ключевые слова: кулоновская энергия, интеграл перекрытия, электронная плотность, радиальное распределение. 

Baranov M.A.

Professor, PhD in physics and mathematics Altay State Technical University

EXACT ANALYTICAL SOLUTION OF THE PROBLEM ON INTERACTION OF ATOMS HAVING SPHERICAL-SYMMETRICAL ELECTRONIC SHELLS

Abstract

Balance of charges of different signs forming atoms makes illegitimate application of approximated and numerical methods to definition of energy of coulomb interactions of atoms. Exact analytical expressions of this energy are resulted for atoms which electronic shells are described by arbitrary functions of radial distribution of electronic density. Quantum corrections are considered. Given expressions open an opportunity of establishment of direct connections between indicators of properties of substances and parameters of functions of radial distribution of electronic density in shells of atoms forming these substances.

Keywords: coulomb energy, overlap integral, electronic density, radial distribution.

ВВЕДЕНИЕ

К настоящему времени доказано, что почти во всех уголках Вселенной, доступных нашему наблюдению присутствует вещество, сформированное атомами сравнительно небольшого числа химических элементов. Достижения химии и даже простое созерцание окружающих нас явлений доказывают, что бесчисленное многообразие свойств веществ обусловлено не только их химическим составом, но во многом и связями между образующими их атомами. Устойчивость же самих атомов крайне удивительна. По крайней мере, естественное и искусственное взаимопревращение элементов в условиях Земли имеет место в ничтожнейших объёмах по сравнению с теми, которые охватываются химическими реакциями или жизненными процессами. Под устойчивостью атомов обычно понимается неизменность конфигураций их электронных оболочек. Именно они, в конечном счёте, оказываются ответственными за многообразие свойств веществ. В этой связи воссоздание конфигураций электронных оболочек является необходимым условием для адекватного решения актуальных задач описания, прогнозирования, моделирования и программирования свойств веществ. Конфигурации электронных оболочек могут быть воссозданы исходя из принципа Паули. Альтернативный подход заключается в том, чтобы в качестве исходного постулата непосредственно принять неизменность и идентичность конфигураций электронных оболочек атомов одного и того же химического элемента. В любом случае для решения указанных выше задач необходимо установление количественных законов взаимодействия атомов. Существующей классификации различных типов связей и знания законов валентности для этого уже недостаточно. При этом возникает необходимость вникать в строение электронных оболочек атома, опираясь не только на его номер в периодической системе, но и на имеющуюся совокупность экспериментальных фактов.

ЭЛЕКТРОСТАТИЧЕСКАЯ ЭНЕРГИЯ

Общепризнанно, что стационарные состояния электронов в атомах могут быть найдены в результате решения уравнения Шрёдингера. Такая задача для свободных атомов и ионов решена [1]. Соответствующие волновые функции представлены слетэровскими функциями – в виде произведений степенной функции и экспоненты. Применение же уравнения Шрёдингера к описанию взаимодействия атомов представляется неоправданно сложным, что заставляет прибегать к всевозможным упрощениям (методы сильной и слабой связи, МТ потенциала и др.) и последующим применениям приближённых и численных методов. Между тем, бесчисленные факты свидетельствуют о том, что взаимодействия атомов обусловлены главным образом балансом электростатического притяжения и отталкивания между их ядрами и электронными оболочками [2]. Следовательно, в основу адекватного описания межатомных взаимодействий должен быть положен закон Кулона. Для дальнейшего анализа необходимо отметить важнейшие, хотя и воспринимаемые в настоящее время как само собой разумеющиеся и даже наивные свойства кулоновских взаимодействий. Во-первых, они парные; во-вторых – консервативные; в третьих – дальнодействующие; в четвертых, в природе имеет место идеальный баланс положительных и отрицательных зарядов. Последнее обстоятельство приводит к тому, что электростатическая энергия взаимодействия двух электрически нейтральных систем, какими, в частности, являются атомы, представляется в виде алгебраической суммы положительной (Е₊) и отрицательной (Е_-) составляющих

  (1)

описывающих взаимодействие одноимённых и разноимённых зарядов соответственно. Эти составляющие огромны и почти полностью компенсируют друг друга. Например, для пары атомов железа, отстоящих друг от друга на расстоянии ~2 Ǻ кулоновская энергия взаимодействия их ядер составляет ~3000 эВ. Величина энергии взаимодействия электронных оболочек примерно такая же. Поэтому абсолютная величина Е₊ и, очевидно, Е_- в данном примере составляет около 6000 эВ. Это примерно в 20000 раз больше экспериментально наблюдаемого значения энергии взаимодействия пары ближайших атомов в кристаллической решётке. Во взаимной компенсации Е₊ и Е_- заключается основная проблема описания кулоновских взаимодействий. Действительно, ничтожное изменение конфигураций электронных оболочек атомов в целом нейтральной системы приведёт и к относительно ничтожным изменениям как положительной, так и отрицательной составляющих кулоновской энергии. При этом энергия взаимодействия системы зарядов системы может измениться как в положительную, так и в отрицательную сторону. По сравнению же с Е^С₁₂ величина этого изменения может оказаться вовсе не ничтожной, а очень даже существенной. Данное обстоятельство свидетельствует о чрезвычайной чувствительности кулоновской энергии нейтральной системы к перераспределению в ней заряда и во многом объясняет трудности предвидения, а зачастую и непредсказуемость результата кулоновских взаимодействий. Вместе с межатомными взаимодействиями чрезвычайно чувствительными к изменениям конфигураций оболочек оказываются и показатели свойств веществ.

С точки зрения математики сказанное означает возникновение неопределённости типа ∞-∞. То есть, при определении каким-либо образом вкладов Е₊ и Е_- и их последующем сложении имеет место потеря нескольких первых значащих цифр. Поэтому точность определения этих вкладов должна быть такой, чтобы можно было доверять последующим цифрам. Так, ошибка в шестом знаке энергии взаимодействия оболочек пары атомов приводит к ошибке в первом знаке энергии взаимодействия атомов в целом, а ошибка в четвертом знаке Е₊ не позволяет оценить даже порядок величины Е^С₁₂. Применение приближённых методов, в соответствии с их статусом, не позволяет достичь требуемой точности. Единственная возможность решения данной проблемы заключается в строгом доказательстве и последующем применении точных аналитических выражений, описывающих электростатическое взаимодействие атомов в зависимости от их взаимного расположения и конфигураций электронных оболочек.

Формально энергия кулоновского взаимодействия пары атомов сортов 1 и 2 записывается в виде двойного интеграла по пространству от произведения зарядовых плотностей ρ₁ и ρ₂ каждого из атомов, включая и распределения зарядов в ядрах, представляемые обычно дельта - функциями

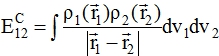  (2)

где  – заряды, сопутствующие атомам 1 и 2 и находящиеся в дифференциально малых объёмах dv₁ и dv₂ вблизи точек, определяемых радиусами-векторами . Поскольку эти векторы зачастую проводятся из центра каждого из атомов, интегралы типа (2) принято называть двуцентровыми или интегралами перекрытия. Соотношение (2) часто приводится в литературе, но непосредственно к численным расчётам оно, как правило, не применяется. В связи с отмеченной выше проблемой требование аналитической интегрируемости (2) превращается из второстепенного [3] в принципиальное. Для упрощения записей в соотношении (2) и в дальнейшем, вплоть до выполнения численных операций будет подразумеваться система единиц, в которой заряд измеряется в элементарных зарядах, расстояния в ангстремах, а коэффициент пропорциональности в законе Кулона равен единице.

СФЕРИЧЕСКАЯ СИММЕТРИЯ

Симметрия равновесной конфигурации электронной оболочки атома должна соответствовать симметрии одной из точечных групп. Простейшей точечной группой является группа сферы или шара SO(3). Распределение электронной плотности в сферически-симметричной оболочке задаётся функцией радиального распределения (ФРР) ρ(r). По физическим соображениям она должна быть положительно определённой и нормированной на заряд n, который в случае нейтрального атома должен совпадать с зарядом ядра.

   (3)

Квантово-механические представления о существовании различных энергетических состояний электрона в оболочке, а также вид рассчитанных волновых функций для свободного атома или иона [1] свидетельствуют о присутствии максимумов на функции радиального распределения. Количество этих максимумов, их расположение, высота и степень размытости индивидуальны для атомов и ионов каждого химического элемента. В конечном счёте, свойства веществ определяются именно деталями профилей ФРР образующих их атомов. Вероятнее всего, стабильные соединения формируются при попадании ядер одних атомов в положения максимумов электронной плотности других. В то же время, множество явлений, как, например, отклонения от соотношений Коши для кубических кристаллов не укладывается даже в рамки модели произвольных сферически симметричных оболочек. Взаимодействия атомов, имеющих сферически-симметричные оболочки, являются не только парными по своей природе, но и центральными. Под центральностью понимается то, что в системе сил взаимодействия пары атомов отсутствует вращающий момент, а линия действия главного вектора этих сил проходит через их ядра. Для произвольных ФРР не существует аналитического представления двуцентровых интегралов типа (2). В этой связи, электронную оболочку в целом необходимо представить в виде суперпозиции подоболочек, а ФРР – в виде линейной комбинации простых базисных функций (БФ) B_i(r), каждая из которых описывает единственный максимум и имеет смысл плотности вероятности (пси-квадрата), соответствующей i-му энергетическому состоянию.

  (4)

где q_i – коэффициенты разложения, понимаемые как заряды подоболочек. Условие нормировки БФ    (5) Из (3) – (5) следует, что    (6)

Адаптивность ρ(r) к реальным распределениям в атомах и возможность решения обозначенной выше проблемы может быть достигнута лишь при выполнении следующих требований к БФ: 1) непрерывность; 2) гладкость; 3) положительная определённость; 4) асимптотическое убывание на бесконечности; 5) наличие единственного максимума, положение и степень размытости которого не ограничены и определяются параметрами БФ; 6) существование точного аналитического представления интегралов типа (2). Часто используемые функции Слэтера типа  не удовлетворяют 5 му и 6 му требованиям. С их помощью не удаётся, например, расположить острый максимум на большом расстоянии от ядра, что, в свою очередь, исключает из рассмотрения широкий класс межатомных связей, реализующихся, например в диэлектриках. Предлагаемый вид БФ следующий [4-5]:

  (7)

где α_i и R_i – параметры. Возможно, что функции вида (7) не единственные, которые удовлетворяют всем вышеперечисленным требованиям, но других примеров пока нет. Вследствие сферической симметрии в положении ядра (r = 0) БФ достигает минимального значения

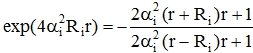   (8) Положение единственного максимума находится из условия равенства нулю первой производной БФ при r>0   (9) Подстановка явного вида (7) в (9) приводит соотношению    (10)

Левая часть (10) положительно определённая. Числитель правой части положительно определённый. Следовательно, решение (10) достигается при отрицательном значении знаменателя, то есть, при r<R_i. Поскольку экспонента намного превышает свой показатель, то левая часть (10) намного превышает величину 4α_i²R_ir, которая, в свою очередь, близка к значению числителя правой части. В целом же соотношение (10) выполняется, когда знаменатель правой части отрицателен, и близок к нулю, т.е. r ≈<R_i.

   (11)

Максимум БФ достигается при    (12)

При больших R_i и α_i положение максимума находится на сфере радиусом R_i. При α_i→∞ подоболочка, описываемая B_i(r) , превращается в тонкую заряженную сферу радиусом R_i. При R_i=0 положение максимума попадает на ядро и совмещается с центральным минимумом. БФ в этом случае превращается в функцию Гаусса

   (13)

Таким образом, адаптивность БФ к реальным распределениям достигается варьированием параметров R_i и α_i. БФ может быть как размытой, что характерно для атомов металлов, так и сильно локализованной на определённом расстоянии от R_i от ядра, что характерно для атомов металлоидов.

ВЗАИМОДЕЙСТВИЕ АТОМОВ

Рассмотрим теперь пару атомов со сферически симметричными, но, вообще говоря, различными оболочками. В этом случае к БФ потребуется добавить ещё один индекс, соответствующий номеру атома из пары (1 или 2). Энергия кулоновского взаимодействия пары атомов, центры которых расположены на расстоянии R друг от друга, представляется в виде

   (14)

где  – потенциал 1i подоболочки.  – энергия кулоновского взаимодействия сферически симметричного электронного облака, распределённого в пространстве по закону B_1i(r) с единичным точечным зарядом, находящимся на расстоянии R от его центра. Аналогично определяется и . –энергия кулоновского взаимодействия двух сферически-симметричных облаков, распределённых по законам B_1i(r) и B_2j(r) и находящихся на расстоянии R между их центрами. Потенциал электронного облака находится с помощью теоремы Остроградского-Гаусса

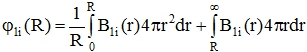    (15)

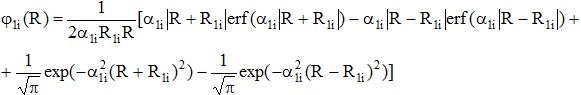и без труда допускает точное аналитическое представление     (16)

Очевидно, что при бесконечном удалении сферически-симметричного облака оно уподобляется точечному заряду, а энергия его кулоновского взаимодействия с единичным точечным зарядом устремляется к 1/R. Действительно, при R→∞ интегралы ошибок обращаются в единицы, а экспоненты в нули.

  (17) Энергия кулоновского взаимодействия между собой двух сферических облаков, распределённых по законам B_1i и B_2j, находится путём интегрирования   (18)

где R – расстояние между центрами облаков, r₁ и r₂ – расстояния от их центров до точки интегрирования. Для соотношения (18) также существует точное аналитическое представление, хотя оно является более громоздким по сравнению с (16). Его доказательство, в отличие от (16) также длительно и громоздко.

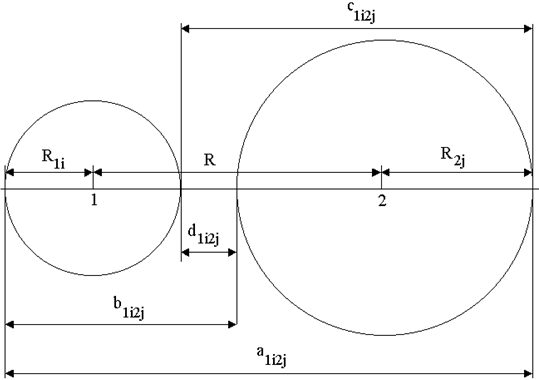
Рис. 1 - Взаиморасположение сфер радиусами R_1i и R_2j, при взаимодействии сферически-симметричных облаков, распределённых по закону (7)

Для того чтобы привести явный вид функции Φ_1i2j проведём сферу радиусом R_1i из центра первого атома и сферу радиусом R_2j из центра второго атома (рисунок 1). На рисунке 1 введены следующие обозначения:

Для дальнейшего сокращения записей обозначим a=a_1i2j; b=b_1i2j; c=c_1i2j; d=d_1i2j; β=β_1i2j. С учётом введённых обозначений появляется возможность представить точное аналитическое выражение для энергии взаимодействия электронных облаков, описываемых БФ вида (7)

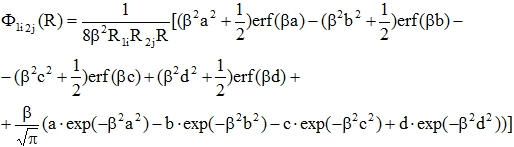   (24)

Очевидно, что при стремлении расстояния между центрами базисных распределений к бесконечности, они уподобляются точечным зарядам, а энергия их электростатического взаимодействия устремляется к 1/R. Действительно, в этом случае все интегралы ошибок обратятся в единицы, а экспоненты – в нули. Поэтому при R→∞

   (25)

С учётом того, что R>>R_1i и R>>R_2j от знаков модулей в (20) – (22) можно отказаться. Тогда выражение в квадратных скобках окажется равным 8R_1i R_2j, а интеграл перекрытия (25) устремится к 1/R.

КВАНТОВЫЕ ПОПРАВКИ

Реалистичные модели межатомных связей, разумеется, должны учитывать влияние и квантовых эффектов. Поскольку в формировании квантовых вкладов в энергию межатомных взаимодействий участвуют только электроны, то упомянутая выше проблема противоположных знаков зарядов не возникает. Это означает, что ничтожное перераспределение электронной плотности приведёт к ничтожным же изменениям квантового вклада в энергию взаимодействия атомов. В этом смысле квантовый вклад правомерно рассматривать в качестве поправки и применять для её определения приближённые методы. Точного аналитического выражения для энергии взаимодействия атомов, обусловленной квантовыми эффектами подобного (2), как это имеет место в электростатике, не существует. Плотность «квантовой» энергии приближённо выражается через электронную плотность в виде [6]

   (26)

Первое слагаемое в правой части (30) представляет собой плотность кинетической энергии электронов обусловленную принципом Паули, а второе – плотность т.н. «обменной» энергии. χ_k и χ_a – коэффициенты. Единого мнения по вопросу определения значений этих коэффициентов нет [7] и дискуссия продолжается. Дробные показатели электронной плотности являются косвенным свидетельством многочастичного характера квантовых поправок. Поскольку количественное описание многочастичных взаимодействий и его последующее применение представляются неоправданно сложными, то остаётся вновь прибегнуть к приближённым методам и ограничиться рассмотрением лишь парных перекрытий электронных оболочек. Квантовую поправку к энергии взаимодействия атомов 1 и 2, расположенных на расстоянии R друг от друга запишем в виде

   (27)

где r₁ и r₂ – расстояния от центров базисных распределений до точки интегрирования (рисунок 1), Ψ_1i2j –интеграл перекрытия БФ.    (28)

Таким образом «погрешности в определении квантовых поправок» могут быть скомпенсированы удачным подбором коэффициента χ_q в (27). После подстановки в (28) явного вида (7) БФ и применения аналитических и спекулятивных приёмов удаётся получить следующий вид интегралов перекрытия

  (29)

Окончательное выражение для энергии взаимодействия атомов сортов 1 и 2 получается путём объединения (14) – (16), (18) – (24) и (27) – (29). ЗАКЛЮЧЕНИЕ

Таким образом, для адекватного количественного предвидения свойств веществ необходимо воссоздание профилей ФРР. Поскольку результирующая электронная плотность представима в виде (4), а БФ – в виде (7), то данная задача сводится к определению наборов параметров {q_i, α_i, R_i} для каждого химического элемента. Возможны два альтернативных подхода к определению этих наборов параметров – первопринципный и эмпирический.

Первопринципный подход предполагает аппроксимацию распределений, заранее рассчитанных из первых принципов функциями вида (7). Однако, как отмечалось выше, малейшие отклонения построенных таким образом распределений от реальности и коварство электростатических сил могут привести к существенным отклонениям ожидаемых показателей свойств веществ от соответствующих экспериментальных данных. Остаётся либо оставить полученный набор параметров неизменным либо принять его за основу с тем, чтобы затем исправить на предмет соответствия эксперименту. Первопринципность при этом, естественно, будет утеряна.

Что же касается эмпирического подхода, то наиболее предпочтительным вариантом был бы непосредственный «промер глубин» электронной плотности в отдельно взятом атоме. Но отсутствие инструмента, позволяющего проводить подобные измерения с достаточной точностью, заставляет провести привязку наборов {q_i, α_i, R_i} к имеющимся экспериментальным данным. В качестве таковых могут быть геометрические параметры молекул и кристаллических решёток, собственные частоты колебаний атомов, энергии фазовых превращений и др. Принципиальная особенность такого подхода заключается в том, что {q_i, α_i, R_i} являются уже не отвлечёнными параметрами правдоподобных потенциальных функций, а несущими физический смысл представителями объективной реальности – распределений электронной плотности в оболочках атомов. Данное обстоятельство, в свою очередь, делает правомерным определение параметров ФРР из экспериментальных данных об одних веществах и применения их к другим, но содержащим те же атомы. Вполне вероятно что на начальном этапе из-за нехватки экспериментальных данных построенные таким образом ФРР окажутся «усреднёнными, сглаженными» по сравнению с имеющими место в действительности. Однако по мере привлечения и обработки всё большего числа фактов о соединениях, содержащих заданный химический элемент вуаль с соответствующей ФРР будет сниматься, а на её профиле проявятся характерные максимумы без которых невозможно адекватное описание всей совокупности наблюдаемых свойств веществ. Представление, например, оболочек атомов металлов в виде всего лишь одной внутренней и одной внешней подоболочкой в виде (7) [8-11] позволило адекватно описать состояния кристаллических решёток в сплавах сложного химического состава.

Материалы доказательного и аналитического характера, в частности, вывод соотношений (24) и (29) из-за их огромного объёма здесь не представлены, но они могут быть опубликованы, как только в этом возникнет потребность.

Литература

1. Clementi E., Roetti C. Roothan-Hartree-Fock atomic wavefunctions // Atomic Data and Nucl. Data Tables. – 1974. – v. 14. – N 3-4. – p. 177-478.
2. Киттель Ч. Введение в физику твёрдого тела. – М.: Наука, 1978. – 792 с.
3. В.Е. Зализняк, О.А. Золотов. Универсальный потенциал взаимодействия для чистых металлов // Наносистемы: физика, химия, математика. – 2012. – 3(1). – с. 76-86.
4. Баранов М.А. Сферическая симметрия электронных оболочек атомов и стабильность кристаллов // ЭФТЖ. - т.1. - в.1. - с. 34-48. http://eftj.secna.ru/ 0501/06013r.pdf.
5. Баранов, М.А. Воссоздание конфигураций электронных оболочек атомов на основе эмпирических данных // Ползуновский вестник. – 2012. – № 2/1.-С. 7-11.
6. Гомбаш П. Статистическая теория атома и её применение. – М.: ИЛ, 1951. – 399 с.
7. Слетэр Дж. Методы самосогласованного поля для молекул и твёрдых тел. – М.: Мир, 1978. – 662 с.
8. Баранов М.А., Дубов Е.А. Поля атомных смещений в кристаллах неупорядоченных сплавов ХН35ВТ И ХН35ВТЮ // Физика металлов и металловедение. – 2007. – т. 104. - № 3. – с. 314-318.
9. Баранов М.А., Щербаков В.М., Черных Е.В., Романенко В.В. Взаимосвязь механических свойств неупорядоченных гамма-фазных сплавов с состоянием их кристаллических решеток // Фундаментальные проблемы современного материаловедения. – 2009. – т. 6. – № 2. – с. 99-106.
10. Baranov M.A., Shcerbakov V.M. Simulation of Multicomponent Crystal States as Tool of Forecasting and Programming of Mechanical Properties of Alloys. // Journal of Materials Science and Engineering. A. – 2011. – v.1. – N 3. - p. 398-407.
11. Баранов М.А., Щербаков В.М. Роль превалирующей фазы в формировании механических свойств сплавов сложного химического состава // Международный научно-исследовательский журнал. – 2013. – ч.1. – т. 7(14). – с. 5-7.