ТЕПЛОВАЯ ИНТЕРФЕРЕНЦИЯ ЭЛЕМЕНТОВ ТРУБНЫХ РЕШЕТОК В ГРУНТОВОМ МАССИВЕ
Курицын Б.Н.1, Кузнецов С.С.2, Бычкова И.М.3
1Доктор технических наук, профессор;
2ассистент;
3магистрант,
Саратовский государственный технический университет имени Гагарина Ю. А.
ТЕПЛОВАЯ ИНТЕРФЕРЕНЦИЯ ЭЛЕМЕНТОВ ТРУБНЫХ РЕШЕТОК В ГРУНТОВОМ МАССИВЕ
Аннотация
В статье излагаются материалы теоретических исследований теплового взаимодействия между грунтовым массивом и системой трубопроводов, приводятся результаты экспериментальной апробации математических моделей на установке электротеплового моделирования.
Ключевые слова: грунт, трубная решетка, тепловая интерференция, моделирование.
Kuritsin B.N.1, Kuznetsov S.S.2, Bichkova I.М.3
1Doctor of technical sciences, professor;
2assistant professor;
3master,
Saratov State Technical University named after Gagarin Yu. A.
THERMAL INTERFERENCE OF ELEMENTS OF TUBE PLATES IN THE EARTHEN ARRAY
Abstract
The article contains materials of theoretical researches of thermal interaction between the earthen array and system of pipelines are used, results of experimental approbation of mathematical model of installation on electrothermal modeling are given.
Keywords: ground, tube plate, thermal interference, modeling.
В современной практике инженерного оборудования зданий все более широкое применение находят трубчатые грунтовые теплообменники. Они используют природное тепло (холод) грунтового массива в установках теплонасосного отопления и горячего водоснабжения, в системах приточной вентиляции для нагрева (охлаждения) воздуха, в установках естественной регазификации сжиженных газов и в других технических решениях [1, 2, 3].
Рациональное размещение грунтового теплообменника на территории, прилегающей к зданию, требует изучение такого важного вопроса, как тепловая интерференция элементов теплообменника при различных вариантах его компоновки. В целях компактности теплообменник может быть выполнен в виде змеевика (регистра) из труб, уложенных в грунте параллельно на определенном расстоянии друг от друга.
Взаимное тепловое влияние труб (тепловая интерференция) снижает удельный теплоприток (удельную холодопроизводительность) в расчете на 1 м трубопровода. Количественно этот эффект можно учесть с помощью коэффициента µ, который представляет собой отношение удельного теплопритока на единицу длины трубной решетки к удельному теплопритоку на единицу длины одиночного трубопровода.
Сформулируем задачу следующим образом. В однородном полуограниченном массиве (грунте) теплопроводностью λ на глубине h заложена цепочка из n цилиндрических труб длиной l и радиусом r0. Трубы расположены параллельно с шагом S так, как это показано на рис. 1. На поверхности труб поддерживается постоянная температура tтр, на поверхности массива – температура tгр. Температурный градиент по глубине массива и фазовые превращения воды в грунте отсутствуют.
Для решения задачи воспользуемся принципом квазистационарных тепловых состояний в сочетании с методом средних потенциалов (метод Г. Хоу) [2, 4]. В качестве исходной предпосылки примем следующие допущения: l>>r0 и h>>r0.
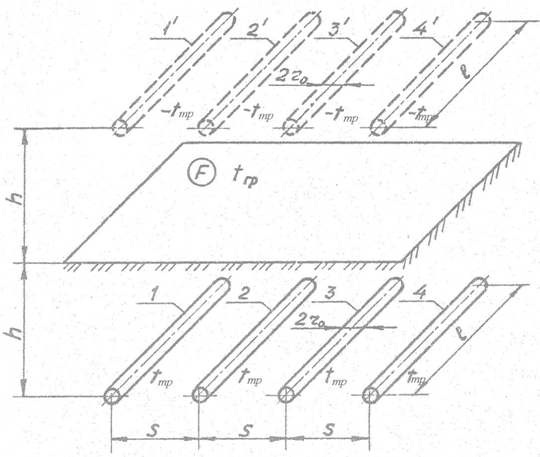
Рис. 1 - К расчету тепловой интерференции трубных решеток в грунтовом массиве
Считая, что тепловой поток распределен по поверхности трубопровода равномерно с линейной плотностью q, запишем уравнение, определяющее среднеинтегральную разность температур между грунтом и поверхностью одиночного трубопровода [4]:
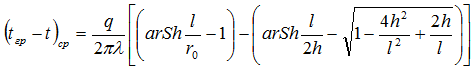 (1)
(1)
Перепишем (1) следующим образом:
![]() (2)
(2)
Где ![]() - геометрические параметры, характеризующие тепловое взаимодействие самой трубы и ее отображения.
- геометрические параметры, характеризующие тепловое взаимодействие самой трубы и ее отображения.
Уравнение (2) можно распространить также на цепочку из n параллельных труб конечной длины.
Тогда среднеинтегральная разность температур между грунтом и поверхностью k-й трубы будет иметь следующий вид:
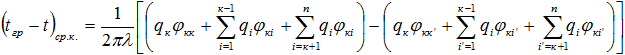 (3)
(3)
Где ![]() - геометрические параметры, характеризующие взаимодействие k-й трубы и ее отображения;
- геометрические параметры, характеризующие взаимодействие k-й трубы и ее отображения;
![]() - геометрические параметры, характеризующие воздействия i-й трубы и ее отображения на k-ю трубу;
- геометрические параметры, характеризующие воздействия i-й трубы и ее отображения на k-ю трубу;
![]() - линейная плотность теплового потока на поверхностях i-й и k-й труб.
- линейная плотность теплового потока на поверхностях i-й и k-й труб.
Причем, на основании (1) и (2):
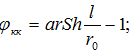 (4)
(4)
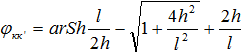 (5)
(5)
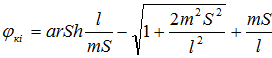 (6)
(6)
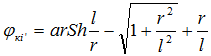 (7)
(7)
где S – расстояние между трубами;
m – число пролетов между k-й и i-й трубами;
r – расстояние между k-й трубой и отображением i-й трубы, определяемое по формуле
![]() (8)
(8)
Аналогичные выражения можно записать для остальных труб решетки. Полагая , приходим к системе из n-линейных уравнений:
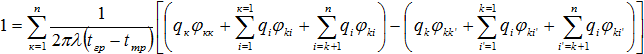 (9)
(9)
решая которую, находим линейную плотность теплового потока на поверхности трубопроводов:
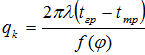 (10)
(10)
Где ![]() - функция от геометрических параметров трубной решетки.
- функция от геометрических параметров трубной решетки.
Общий теплоприток ко всем трубам решетки:
![]() (11)
(11)
Величину удельного теплопритока для одиночного трубопровода эквивалентной длины L=nl получим по формуле (1) при ![]()
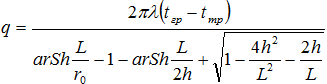 (12)
(12)
В частном случае при l >>h уравнение (12) принимает вид:
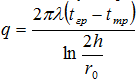 (13)
(13)
Общий теплоприток для всей длины одиночного трубопровода:
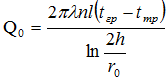 (14)
(14)
Коэффициент µ, учитывающий снижение теплопритока вследствие тепловой интерференции элементов трубной решетки:
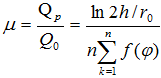 (15)
(15)
Система уравнений (1÷15) формирует математическую модель тепловой интерференции грунтовых теплообменников с горизонтальным расположением трубной решетки. Предложенная модель удобна для программирования и успешно реализуется средствами вычислительной техники.
В качестве практического применения предложенной математической модели (1-15) оценим тепловую интерференцию элементов грунтового теплообменника со следующими геометрическими параметрами: r0=0,011 м, h=2,5 м; l=6,0 м. Результаты расчетов для трубных решеток с числом элементов n=2 и 6 при шаге между трубами S от 0,25 до 2,0 м представлены на рис. 2.
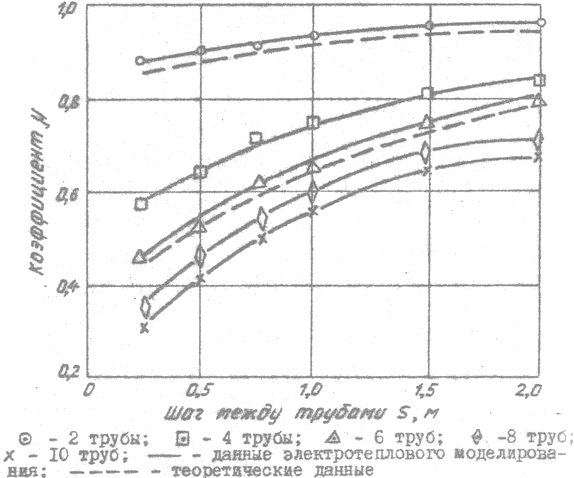
Рис. 2 - Значения коэффициента µ для трубных решеток в грунтовом массиве
Для сравнения на том же графике приводятся экспериментальные данные, полученные на установке электротеплового моделирования. Как видно из графика, результаты расчетов хорошо согласуются с данными экспериментальных исследований. Среднее расхождение результатов составляет 6,8 %; причем, как правило, теоретические расчеты дают более низкие значения коэффициента µ. Такое соотношение вполне оправдано, если учесть, что применение метода среднего потенциала обычно предопределяет заниженную величину расчетного теплопритока [4].
Использование предложенной математической модели в инженерной практике способствует совершенствованию методов расчета и проектирования трубчатых грунтовых теплообменников и повышает качество проектных проработок.
Литература
- Курицын Б. Н., Юшин А. Н. Грунтовые теплообменники в системах инженерного оборудования зданий // Научно-технический калейдоскоп. – Ульяновск: Издательство УлГТУ. – 2001. – № 10. – С. 65-67.
- Курицын Б. Н., Павлутин М. В., Осипова Н. Н. Испарительные установки сжиженного газа с трубчатыми грунтовыми теплообменниками // Инженерные системы: АВОК-Северо-Запад. – № 1 (27). – 2007. – С. 48-51.
- Курицын Б. Н., Осипова Н. Н. Использование природного холода грунта в системах бытового кондиционирования воздуха // Научно-технические проблемы совершенствования и развития систем газоэнергоснабжения. Сборник научных трудов. – Саратов: Издательство СГТУ. – 2006. – С. 196-203.
- Иоссель Ю. А. Расчет потенциальных полей в энергетике. – Спб.: Энергия. – 1998. – 350 с.
