МОДЕЛЬ КАМЕРЫ

Шуляев А.В.

Аспирант,

Воронежский институт высоких технологий

МОДЕЛЬ КАМЕРЫ

Аннотация

Цель статьи предоставить аналитическое описание модели камеры, позволяющей количественно связать отношения между некоторой точкой реального трехмерного мира и ее проекцией на двухмерную плоскость изображения.

Ключевые слова: внутренняя матрица, внешняя матрица, дисторсия, пинхол.

Shuljaev A.V.

Postgraduate student,

International Institute of High Technologies

CAMERA MODEL

Abstract

The purpose of the article is to provide an analytical description of the camera model which allows to estimate quantify the relationship between some point in real three-dimensional world and its projection onto a two-dimensional image plane.

Keywords: intrinsic matrix, extrinsic matrix, distortion, pinhole.

Первой камерой считается обскура, она была изобретена в XVI веке и представляла собой ящик с очень маленьким отверстием на своей фронтальной плоскости, внутри ящика свет, прошедший через отверстие проецировался на заднюю стенку. Изображение при этом получалось перевернутым, а величина проекции зависела от расстояния до проецируемого объекта. Камера-обскура демонстрировала законы перспективы. Математическая модель камеры-обскуры, или как ее еще называют, пинхол, подразумевает, что отверстие бесконечно мало, в реальности это конечно не так, более того, в современных камерах имеется сложная система линз призванных доставлять на светочувствительные элементы камеры больше света. Однако, такая грубая модель вполне успешно применяется в компьютерном зрении, в том числе и для высокоточных измерений в трехмерном пространстве [1]. Такие измерения применяются в фотограмметрии – научно-технической дисциплине, занимающаяся определением характеристик, взаимного расположения объектов по их фотографиям снятым с различных летательных аппаратов, измерения в трехмерном пространстве с помощью различных светочувствительных датчиков, в том числе и камер, широко применяется на производстве в задачах автоматической инспекции и сборки.

На Рис. 1 можно видеть, как точка P с мировыми координатами  проецируется на плоскость изображения  в точку  с координатами .

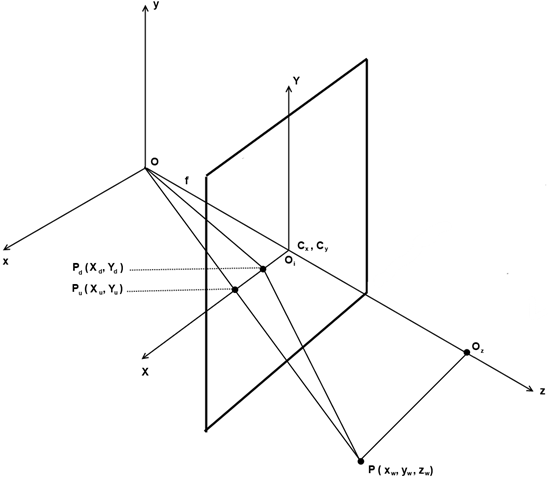
Рис. 1 – Геометрия камеры с учетом радиального искажения

Такое преобразование задается уравнениями перспективной проекции:

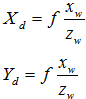                                               (1)

где f фокусное расстояние, определяемое кривизной линзы.

Оптическая ось Oz перпендикулярна плоскость изображения и пересекает ее в некоторой точке, которая в идеальном случае совпадает с центром изображения . Однако, в действительности, из-за асферичности поверхности линз, дефектах при сборке камеры и других технических проблемах это не так, именно поэтому координаты центра изображения входят в список параметров, которые должны быть откалиброваны. Среди параметров модели камеры выделяют две группы.

Внутренние параметры

Эта группа параметров описывает геометрию камеры, они не обходимы для преобразований на плоскости изображения, т.е. в 2D. Сюда входят, координаты центра изображения , фокусное расстояние f и коэффициенты дисторсии.

В своей работе [2] Janne Heikkilä и Olli Silvén записали внутренние параметры камеры в виде матрицы:

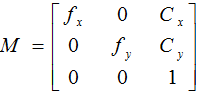                                              (2)

Использование линз в оптических системах приводит к различным аберрациям. Как правило, самой сильной и, в то же время, легко устранимой аберрацией является радиальная дисторсия. Она обусловлена тем фактом, что фокусное расстояние в разных частях линзы отличается.

Радиальная дисторсия моделируется следующим образом 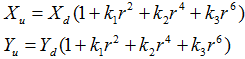[3]:

                               (3)

где .

Как правило, достаточно коэффициентов первого порядка, т.е. к параметрам модели добавляется два коэффициента дисторсии по X и Y.

Т.о. некоторая точка трехмерного мира может быть преобразована в однородные координаты изображения следующим образом.

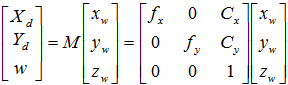                             (4)

В формуле (4) и далее, преобразования выполнены в однородных координатах, а w - фиктивная переменная.

Внешние параметры

Эта группа параметров описывает положение камеры в пространстве, ее ориентацию. Цель этой группы параметров связать мировые координаты, с системой координат камеры. В евклидовом пространстве это может быть сделано единственным образом, если ориентация камеры задается как набор углов вращений вокруг собственных осей.

В группу внешних параметров входят 3×3 ортонормированная матрица вращения R и вектор столбец T.

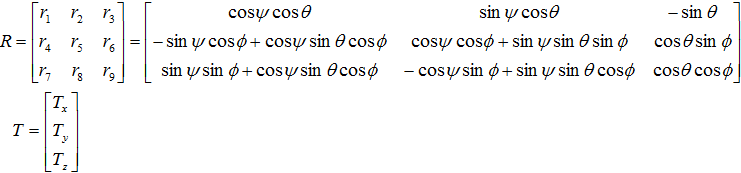
где

 - это углы вращения вокруг осей системы координат,

T - трехкомпонентный вектор параллельного переноса центра координат камеры.

Эта группа параметров может быть представлена в виде матрицы, называемой внешней матрицей камеры:

Т.о. преобразование некоторой точки трехмерного мира в систему координат связанную с камерой производится следующим образом:

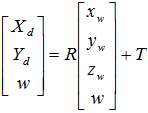                                          (5)

Комбинируя формулы (4) и (5) получим уравнение, которое однозначно связывает некоторую точку изображения в однородных координатах с некоторой точкой реального мира:

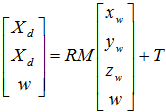                                       (6)

Перед началом работы с любым изображением, полученным с камеры, необходимо провести устранение дисторсии на основе формулы (2) игнорируя коэффициенты большого порядка.

Полученная модель позволяет проводить измерения в трехмерном пространстве с высокой точностью. Предварительно должны быть получены параметры модели камеры, в процессе калибровки. Калибровка камеры – это процесс, позволяющий получить внешние и внутренние параметры камеры, а так же коэффициенты искажений линз. Получение параметров модели камеры, позволяет установить количественные соотношения между некоторой точкой 3D объекта и ее наблюдаемой 2D проекцией на изображении с камеры. Возможны две ситуации:

1. Известна проекция некоторой точки реального мира, но неизвестны трехмерные координаты в системе координат связанной с камерой.
2. Имеются трехмерные координаты некоторой точки в системе координат связанной с камерой, но неизвестна проекция это точки.

Эти ситуация могут быть разрешены откалиброванной моделью камеры с помощью уравнений, описанных выше.

Литература

1. Tsai, R. Y. A Versatile Camera Calibration Technique for High-Accuracy 3D Machine Vision Metrology Using Off-the-shelf TV Cameras and Lenses // IEEE JOURNAL OF ROBOTICS AND AUTOMATION. – 1987. Vol. RA-3, № 4. – P. 343-344.
2. Heikkila, J., Silven O. A four-step camera calibration procedure with implicit image correction // IEEE Computer Society Conference on Computer Vision and Pattern Recognition: труды – 1997 P. 1106.
3. Gary Bradski, Adrian Kaehler. Learning OpenCV. O’Reilly, 2008. C. 375-378