АЛГОРИТМ СИЛОВОГО АНАЛИЗА ШАРНИРНО-СТЕРЖНЕВЫХ МАНИПУЛЯТОРОВ С ПРОСТРАНСТВЕННЫМ ПРИВОДНЫМ МЕХАНИЗМОМ

Бабоченко Н.В.

Кандидат технических наук, доцент,

Волгоградский государственный аграрный университет

АЛГОРИТМ СИЛОВОГО АНАЛИЗА ШАРНИРНО-СТЕРЖНЕВЫХ МАНИПУЛЯТОРОВ С ПРОСТРАНСТВЕННЫМ ПРИВОДНЫМ МЕХАНИЗМОМ

Аннотация

В статье представлен манипулятор с двухзвенной шарнирно- стержневой стрелой и рассмотрен силовой анализ шарнирно-стержневого манипулятора с определением его зоны действия, используя пространственный метод координат, для решения задач направленных на определение силовых характеристик шарнирно-стержневых манипуляторов.  

Ключевые слова: манипулятор, шарниры, стержни, гидроцилиндры, статика.

Babochenko N.V.

Сandidat of the technical sciences, assistant professor,

Volgograd State Agricultural University

ALGORITHM ANALYSIS OF POWER JOINT-BAR MANIPULATOR SPATIAL DRIVE MECHANISM

Abstract

The article presents a manipulator with articulated hinge-rod boom and power analysis considered jointed manipulator rod with the definition of its coverage, using spatial coordinates method for solving aimed at determining the characteristics of power-rod pivotally manipulators.

Keywords: manipulator’s, joints, pivotal, hydrocylinds, static’s.

Шарнирно-стержневые манипуляторы относится к семейству погрузочных манипуляторов с пространственным приводным механизмом [1]. Главной особенностью подобных манипуляторов является наличие двух расположенных под углом друг к другу гидроцилиндров, штоки которых посредством особого шарнирного устройства соединены между собой и со стрелой – её коренной секцией. Противоположные концы (корпуса) этих цилиндров крепятся на основании с помощью шарниров с двумя степенями свободы. Указанные звенья образуют особый пространственный приводной механизм, ведущими звеньями которого являются гидроцилиндры. Цилиндры обеспечивают подъём (опускание) стрелы в вертикальной плоскости и её разворот на углы до ± 65⁰ в горизонтальной плоскости.

Грузовая стрела манипулятора может быть шарнирно-сочлененной, в частности трехзвенной, как это предусмотрено в [1, 2]. Для задействования секций (звеньев) стрелы предусматриваются свои гидроцилиндры, которые работают в плоскости стрелы в обычном порядке. Предлагаемый шарнирно-стержневой гидроманипулятор (рис.1; [1,2]) формально включает двухзвенную шарнирно-сочлененную стрелу. В нём имеются: основание 1, два гидроцилиндра 2 и 3 для подъёма (опускания) и поворота коренной секции 4 и стрелы в целом. Штоки гидроцилиндров также соединены в особом шарнирном устройстве 5 со многими степенями свободы. Вторая секция 6 стрелы (рукоять с крюком на конце) приводится в действие двумя параллельно расположенными гидроцилиндрами 7.

В рассматриваемом манипуляторе сформирован целенаправленный силовой поток – звенья стрелы воспринимают усилия растяжения или сжатия. Обе секции стрелы – это пространственные фермы – большинство их узлов несут определенную функцию. В частности, в шарнирном устройстве 5 соединены между собой не только штоки гидроцилиндров 2 и 3, но стержни коренной секции 4 и корпуса гидроцилиндров 7 рукояти. Манипулятор в целом – вместе с гидроцилиндрами – представляет сложную, но функционально обусловленную пространственную ферму, геометрия которой видоизменяется не только за счёт изменения длины гидроцилиндров, но  и дискретного регулирования длины верхних поясов (стержней) обеих секций стрелы.

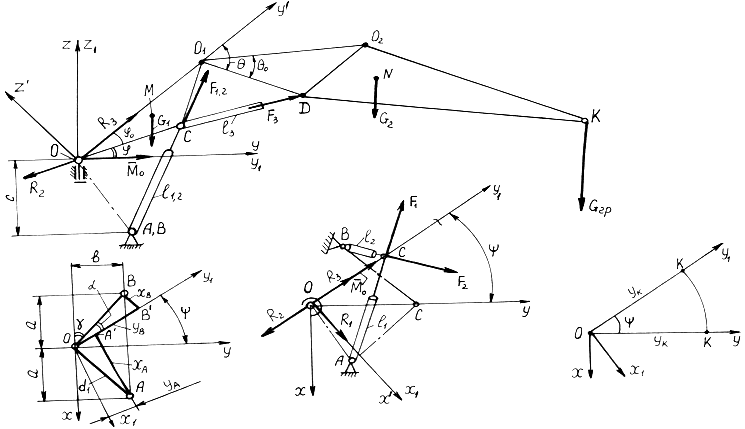
При силовом расчете двухзвенной шарнирно-стержневой стрелы считаются известными координаты точек А (а, в, -с) и В (-а, в, -с) крепления гидроцилиндров пространственного приводного механизма на основании; в выбранных системах отсчёта (рис. 2), координаты опоры О равны нулю. Известны также геометрические размеры двухзвенной шарнирно-стержневой стрелы, длина гидроцилиндров и их ход штока. Плоские фермы треугольников и, в частности, плоская ферма ОС коренной секции (рис. 1) первоначально трактуются как стержни, а при разработке расчётной схемы секции будет учитываться её реальная конструкция.

Требуется определить усилия F₁, F₂, F₃ в штоках гидроцилиндров (параллельные гидроцилиндры СD рукояти рассматриваются как одно кинематическое звено). В числе искомых величин  реакции R₀  и R₀₁ в шарнирах О и О₁ и момент в опорном шарнире О (на рис. 4, показан вектор-момент ). Изменения геометрии стрелы за счёт длины верхних стержней не рассматривается, как не принципиальное [1, 2].

Сначала определяются искомые величины в системе Оx₁y₁z₁, координатная плоскость Оy₁z₁ которой отслеживает поворот стрелы в горизонтальной плоскости на угол y и совпадает с плоскостью стрелы. С учётом того, что коренная секция набрана из стержней, составляющие R₂ и R₃ реакции в опоре О направлены по стержням, а третья составляющая R₁ – перпендикулярно плоскости стрелы – вдоль оси Оx₁.

Благодаря этому схема расчёта коренной секции и системы в целом упрощается – пространственная система сил сохраняется лишь по отношению к усилиям F₁ и F₂ в штоках гидроцилиндров пространственного приводного механизма. С учётом этого координаты x_С и x_К в системе Оx₁y₁z₁ равны нулю.

Составим уравнения равновесия сил и моментов, действующих на шарнирно-стержневую стрелу, в подвижной системе координат Оx₁y₁z₁. При рассмотрении стрелы в целом усилие F₃ в штоках гидроцилиндров рукояти и реакция в шарнире О₁ являются внутренними силами.

С учётом этого имеем:

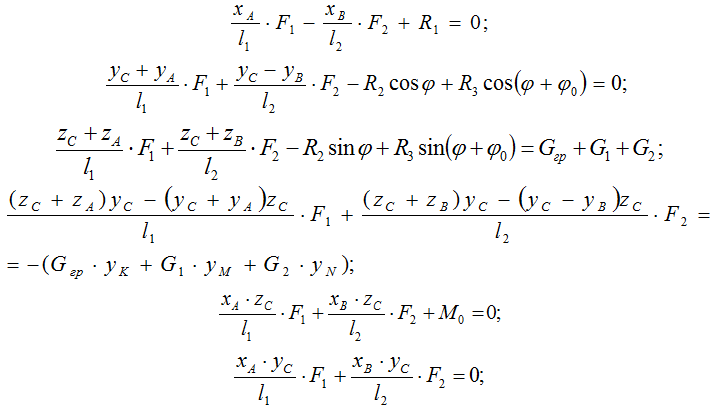    (1)

где y_M, y_N – координаты вдоль оси О y₁ центров коренной секции и рукояти; z_A = z_B = - c (рис. 2).

В результате решения системы алгебраических уравнений (1), определяются искомые величины F₁, F₂, R₁, R₂, R₃, M₀. Во избежание громоздких выражений решение в общем виде не приводится. Вместе с тем, переходя от “затвердевшей” к реальной системе, отметим, что искомые величины являются функциями длины l₁ и l₂ гидроцилиндров и обобщённых координат j и y. Следовательно, полное решение задачи силового анализа – это определение диапазона изменения названных величин, в том числе усилий  F₁ и F₂  в штоках гидроцилиндров.

В отличие от традиционных монолитных коренных секций, здесь сила R_Сx проходит через специальный шарнир С и его цапфы, поэтому не образуется момент закручивания фермы ОС. Сила R_Сx воспринимается поперечным сечением этой плоской фермы, которая, выполнена жёсткой – с перемычками (рис. 1). Сила R₁ является незначительной и замыкается в опорно-поворотном устройстве – в опоре О.

Для определения остальных неизвестных F₃ и R₀₁ можно рассматривать равновесие рукояти в той же системе координат Оx₁y₁z₁, координатная плоскость  Оy₁z₁ которой совпадает с плоскостью стрелы (рис. 2).

Силовой анализ выполняется согласно законам статики. Для рассматриваемого  гидроманипулятора (с плавным и бесступенчатым регулированием скорости перемещения штоков гидроцилиндров, коренной секции, рукояти и груза) коэффициент динамичности к_д = 1,05 … 1,15.

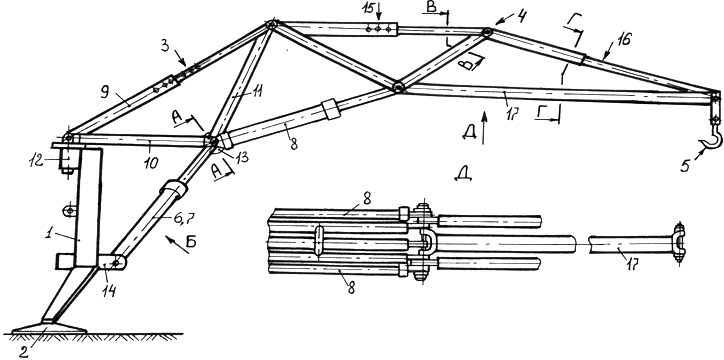
Рис. 1.– Шарнирно-стержневой гидроманипулятор

Рис. 2 – Силовая схема шарнирно-стержневого гидроманипулятора

Литература

1. Кривельская Н.В. Совершенствование сельскохозяйственных шарнирно-стержневых гидроманипуляторов с пространственным приводным механизмом: Дис. … к-та техн. наук / ВГСХА. – Волгоград, 2004. – 196 с.
2. Кривельская Н.В. Совершенствование сельскохозяйственных шарнирно-стержневых гидроманипуляторов с пространственным приводным механизмом: Монография / ВГСХА. – Волгоград, 2010. – 104 с.