Информационно-автономный метод Расширенных микронавигационных измерений В радарах квазинепрерывного излучения при прОизвольной ориентации главного луча
Информационно-автономный метод Расширенных микронавигационных измерений В радарах квазинепрерывного излучения при прОизвольной ориентации главного луча
Аннотация
Для типовых авиационных РЛС квазинепрерывного излучения с «встроенной» инерциально-спутниковой системой микронавигации фазового центра антенны предлагается метод автономных радиолокационных измерений наклонной дальности, радиальных составляющих скорости и ускорения фазового центра, обеспечивающих эффективную коррекцию инерциального канала микронавигации в условиях радиопомех, исключающих возможность использования корректирующих данных от спутниковых навигационных систем. Метод базируется на излучении/обработке сигналов от земли при «бинарных» пачках импульсов с линейной частотной модуляцией несущего колебания, возможностью управления крутизной модуляции и периодом повторения импульсов. Обеспечивается повышение информативности, потенциальной точности, помехоустойчивости сеанса измерений и возможность их реализации вне зависимости от текущих данных и точности инерциальной (микро)навигации/ориентации. Устраняются ограничения по ориентации главного луча РЛС, присущие известным методам измерения дальности/скорости с управлением углом наклона луча, расширяются возможности одновременного решения в РЛС основной функциональной задачи класса «воздух-воздух» и «фонового» выполнения предлагаемым методом радиолокационных измерений в интересах микронавигации РЛС. Представлены аналитические зависимости, результаты модельных и натурных экспериментов, подтверждающие работоспособность и эффективность применения предлагаемого метода.
1. Введение
В современных авиационных радарах с синтезируемой апертурой антенны
, для отслеживания траектории ее фазового центра (ФЦА) используются специализированные инерциально-спутниковые микронавигационные системы (МНС), аппаратно-алгоритмически интегрированные в структуру РЛС , , . Для РЛС Х-диапазона и при меньшей длине волны λ сохраняет актуальность проблема повышения точности МНС , , решение которой в настоящее время усложняется из-за усиления фактора организованных помех для аппаратуры глобальных навигационных спутниковых систем (ГНСС), традиционно используемой качестве высокоточного корректора для инерциальной подсистемы, являющейся функциональным «ядром» типовой МНС , , . Становится уже типичной сигнально-шумовая/помеховая обстановка при применении МНС, практически исключающая возможность использования ГНСС-корректора и растет практическая значимость исследований в области «неспутниковой» микронавигации, в т. ч. связанных с применением нетрадиционных датчиков микронавигационной информации для эффективной коррекции инерциального канала МНС , , при отсутствии данных от ГНСС. В работах , , показаны возможности использования самой РЛС в качестве скоростного корректора собственной «встроенной» МНС и предложены:• адаптивно-робастные (АР) методы измерения радиальной скорости/дальности ФЦА до земли при квазинепрерывном излучении (КНИ) РЛС;
• схемы и процедуры коррекции МНС на основе оценивания ошибок инерциального канала с использованием обобщенного фильтра Калмана (ОФК)
при комплексной обработке инерциальных и радиолокационных (РЛ) измерений.Натурные эксперименты
, , с использованием такой РЛ скоростной коррекции показали, что в РЛ-инерциальном режиме при помехах ГНСС сохраняется работоспособность МНС, но, в сравнении с типовой позиционно-скоростной коррекцией от ГНСС , , , , обеспечивается относительно невысокая точность микронавигации ФЦА. При длительной работе МНС только в таком режиме , , наблюдались случаи неконтролируемого роста ошибок оценивания – практической расходимости ОФК , прежде всего, обусловленной низкой информативностью, наличием «аномалий» (выбросов) первичных РЛ измерений, низкой частотой обновления РЛ информации, высокой динамикой и неопределенностью (параметрической и/или статистической) оцениваемого и измерительного процессов. Традиционные методы , , предполагают контур АР управления ориентацией оси главного луча (ГЛ) диаграммы направленности антенны РЛС, опираясь на текущие измерения МНС и априорные данные об их точности. При этом для наиболее интенсивного эхосигнала от «следа» ГЛ на поверхности обеспечивается его «наблюдаемость» в рабочей зоне периода повторения импульсов (ППИ) и устранение причин неоднозначности измерений по дальности/углу наклона, которая при произвольной ориентации ГЛ может быть обусловлена суперпозицией сигналов от нескольких полос поверхности (ПП) в «следе» ГЛ, дистанцированных на кратное ППИ расстояние. Очевидно, что эффективность такого управления, точность и устойчивость процесса РЛ измерений существенно зависят от «качества» данных от МНС, используемых при управлении ГЛ перед каждым сеансом РЛ измерений. В условиях помех ГНСС типичной является длительная работа МНС в автономном (инерциальном) режиме, с существенным «накоплением» ее ошибок к моменту включения РЛС/назначения РЛ-инерциального режима микронавигации. В таких ситуациях «грубые» ошибки исходных данных для управления ГЛ, получаемых от МНС, не позволяют достичь целей этого управления (в аспектах наблюдаемости и эффекта суперпозиции сигналов), ведут к срывам сеанса РЛ измерений и «аномальным» оценкам траекторных параметров ФЦА, дальнейшее использование которых при скоростной коррекции МНС может быть критичным, практически нарушающим работоспособность МНС. Данные от МНС используются и при определении однозначной дальности , , и их недостаточная точность также может приводить к аномальным (в несколько км) ошибкам в оценках дальности от ФЦА до земли и соответствующим ошибкам в расчетных углах наклона. В целом, существует объективная необходимость в разработке информационно-автономного метода РЛ микронавигационных измерений, эффективность применения которого не зависит от текущих данных МНС и уровня их точности. Кроме того, для повышения эффективности РЛ корректора в условиях интенсивного маневрирования носителя РЛС требуется расширение информативности РЛ измерений, как минимум, за счет измерения радиальной составляющей ускорения ФЦА. С другой стороны, традиционные методы , , для сеанса РЛ измерений требуют специальной ориентации ГЛ, что затрудняет их реализацию одновременно с шагом решения основной функциональной задачи РЛС (например, поиск/обнаружение/сопровождение воздушного объекта на фоне земли), при которой ориентация ГЛ подчиняется другой логике, противоречащей требованиям по ориентации при РЛ измерениях. Как правило, при жестких требованиях к пропускной способности РЛС последовательная комбинация – с разнесением по времени шагов основной задачи и сеансов РЛ измерений для микронавигации – не представляется возможной. Возникает необходимость в разработке метода РЛ измерений, совмещаемого по времени с решением основной задачи РЛС, т. е. реализуемого в «фоновом» режиме при фактически произвольной ориентации ГЛ и параметрах излучения, диктуемых основной задачей РЛС. В данной работе в качестве основной рассматривается вышеуказанная задача класса «воздух-воздух», для решения которой используется режим КНИ с линейной частотной модуляцией несущего колебания (ЛЧМ) , , , , в общем случае, с варьируемой крутизной ЛЧМ и/или длительностью ППИ.Цель данной статьи – представление информационно-автономного метода РЛ измерения дальности, радиальных составляющих скорости и ускорения ФЦА при квазинепрерывном ЛЧМ-излучении и любом направлении ГЛ радара, назначаемом управляющим алгоритмом РЛС при поиске/ обнаружении/ сопровождении маловысотной цели на фоне земли и в окологоризонтном «свободном» пространстве.
Прагматическая цель работы:
• расширение функциональных возможностей РЛС в режимах КНИ с ЛЧМ – в качестве автономного измерителя микронавигационных параметров ФЦА, функционирование которого совмещается (по параметрам КНИ и направлениям ГЛ) с типовыми режимами работы РЛС по маловысотным объектам;
• повышение информативности, помехоустойчивости и точности РЛ микронавигационных измерений в сравнении с типовыми методами;
• обеспечение работоспособности и приемлемой точности РЛ-инерциальной микронавигации ФЦА при организованных помехах ГНСС.
2. Основные результаты
В типовых АР методах
, , РЛ измерения дальности/радиальной скорости ФЦА при КНИ осуществляется по эхосигналам от одной пачки импульсов, излучаемых с высокой/высокой средней ЧПИ . При этом, основываясь на текущих измерениях МНС, их априорно заданных точностных характеристиках, реализуется АР управление наклоном ГЛ, которое должно обеспечить выполнение следующих условий:1) соответствие ПП, с которой пересекается ось ГЛ, дискрету неоднозначной задержки сигнала/дальности (НЗС) в «прозрачной» (рабочей) зоне ППИ;
2) исключение/снижение в рабочих дискретах НЗС в ППИ (вне зон бланкирования приемника), влияния эффекта суперпозиции сигналов от разных ПП в границах облучаемой ГЛ земной поверхности («следа» ГЛ), дистанцированных друг от друга на кратное ППИ расстояние.
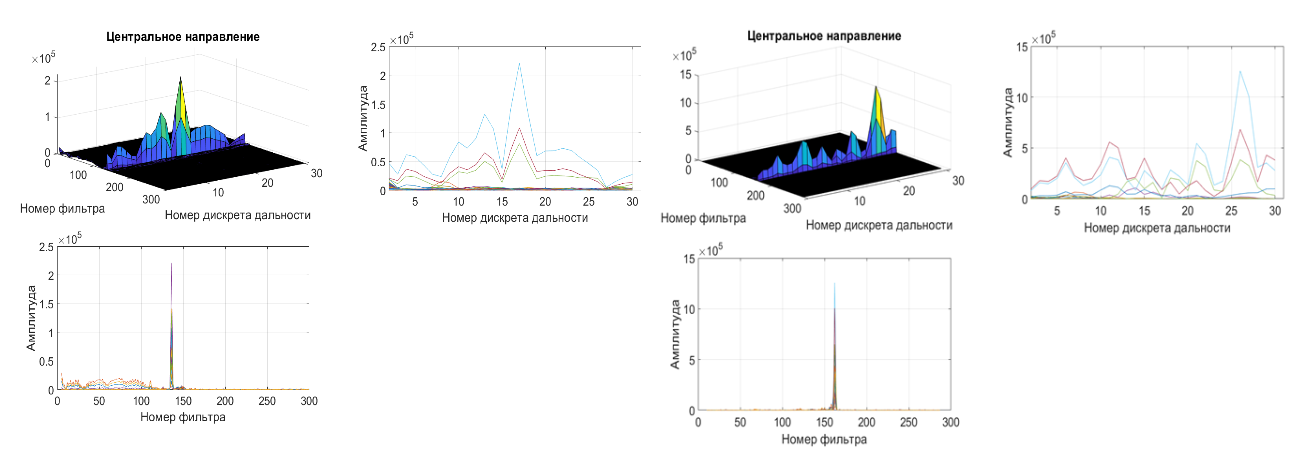
Рисунок 1 - Амплитуды сигнала от следа ГЛ в зависимости от дискрета НЗС (дальности) и номера доплеровского фильтра
• действительный ГМА соответствует «слепой» зоне ППИ (зоне бланкирования) и частотно-временные измерения по ГМА, наблюдаемые в «крайних» дискретах НЗС в ППИ характеризуются «аномальными» погрешностями;
• из-за неустраненной суперпозиции сигналов нескольких ПП (при реальной протяженности следа ГЛ, превышающей расчетную) отсутствует явно выраженный ГМА и измерения по ГМА в ППИ, в общем случае, произвольные, не связанные однозначно с дальностью/углом наклона.
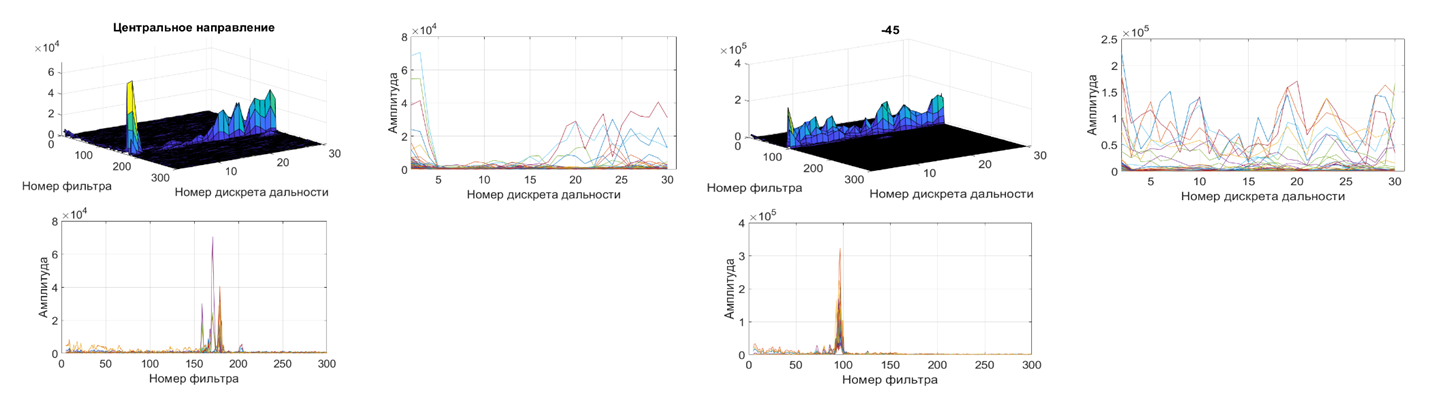
Рисунок 2 - Амплитуды сигналов от следа ГЛ, локальные и глобальные максимумы амплитуды при нарушении условий 1) и 2) вследствие аномальных ошибок в данных МНС, используемых при управлении ГЛ
где
– оценка индекса ППИ Tr на основании данных о геометрической высоте Н* ФЦА над рассматриваемой ПП в следе ГЛ и заданном угле наклона β*при управлении ГЛ, полученных с использованием информации МНС; int (•) – целая часть числа в скобках; с – скорость радиоволны. В типовых методах , , предполагается, что даже при относительно невысокой точности данных от МНС, как минимум, обеспечивается точное определение индекса ППИ вида (3) и, соответственно, однозначное определение дальности (1) на уровне погрешности δτ измерения НЗС и расчетного угла наклона (2) с точностью, которая в виде абсолютной ошибки δβ выражается через абсолютные ошибки δR=(с/2) δτ оценки дальности R и δH определения высоты Н превышения ФЦА над геодезической высотой рассматриваемой ПП в «следе» ГЛ:
Однако, как показали натурные эксперименты при «нештатной» работе МНС и значительной параметрической и/или статистической неопределенности ее ошибок, однозначное определение индекса ППИ (3), дальности (1) и угла (2) во многих случаях практически не обеспечивается. Возникают аномальные оценки радиальной скорости, в основном обусловленные «грубыми» ошибками МНС по углу наклона. Дальнейшее использование таких аномальных оценок для коррекции МНС на основе ОФК очень быстро приводит к практической расходимости фильтрации и, следовательно, только к ухудшению работы МНС. Возникает задача – исключить возникновение аномальных РЛ измерений/оценок, вызванных недостоверными исходными данными МНС, используемыми при управлении ГЛ. Решение, по сути, сводится к разработке информационно автономного (ИА) метода РЛ микронавигационных измерений, слабо зависящего от исходной информации МНС и ее качества, когда даже «грубые» ошибки МНС не оказывают существенного влияния на точность РЛ измерений. Подход к решению, рассматриваемый в работе, основан на использовании ЛЧМ-излучения, при котором достигается «расщепление спектра» принимаемых сигналов от разных дистанцированных ПП в «следах» ГЛ и БЛ – рассредоточение по разным частотам, зависящим от дальностей до каждой конкретной ПП – и тем самым исключается суперпозиция сигналов, ведущая к неоднозначности по дальности/направлению. Предлагается метод РЛ микронавигационных измерений, базирующийся на излучении в заданном направлении ГЛ двух пачек импульсов Рi-1 и Рi при КНИ с ЛЧМ, в общем случае, при варьировании крутизны ЛЧМ S и/или ППИ Tr, т. е. «бинарного пакета» Рi-1 (Si-1; Tri-1)/Рi (Si; Tr), где Si-1 ≠ Si, Tri-1 ≠ Tri, а интервал ΔtМП между началом текущей пачки ti пачки и окончанием предыдущей ti-1+ TРi-1 минимизируется: ΔtМП = ti – (ti-1+ TРi-1) → min, где tРi-1 – длительность пачки Рi-1 в «бинарном пакете». Отметим, что именно такое излучение используется в АР методах наблюдения /сопровождения воздушных объектов
, , , и эти задачи далее рассматриваются как основные задачи РЛС, на фоне выполнения которых и в рамках указанного КНИ с ЛЧМ, одновременно реализуется и предлагаемый метод РЛ измерений.При направленном вниз ГЛ и ЛЧМ излучении с крутизной S наблюдаемый в каждом дискрете НЗС в рабочей зоне ППИ, соответствующем оценке НЗС τ, спектр отраженных сигналов от участков земной поверхности, облучаемых ГЛ и БЛ диаграммы направленности, в общем случае, включает интенсивные составляющие на дальностно-доплеровских частотах (ДДЧ) FRD(j)
где V, W и VH – траекторная, путевая и вертикальная скорости ФЦА, соответственно; φ(j) – угол между вектором траекторной скорости и направлением на j-ую ПП в границах «следов» ГЛ и БЛ, находящуюся на удалении (1) от ФЦА; α – азимутальный угол оси ГЛ относительно вектора путевой скорости; β(j) – угол наклона для направления к j-ой ПП. Соответственно (2) в спектре сигнала наблюдаются ГМА и локальные максимум амплитуды (ЛМА), каждый из которых однозначно соответствует определенной дальности до ПП, причем ПП удалены друг от друга на кратную ППИ дистанцию.
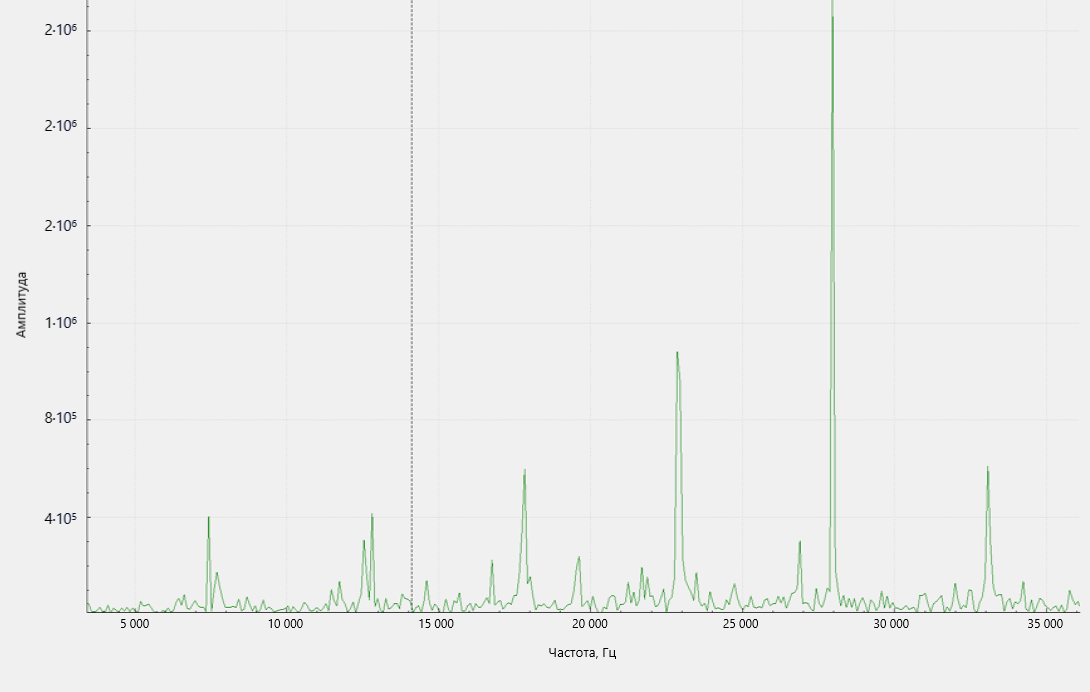
Рисунок 3 - Типичный спектр отраженного от земли ЛЧМ-сигнала в дискрете НЗС с ГМА, наблюдаемым в ППИ
• оценка НЗС τi-1, соответствующая тому дискрету НЗС в ППИ, в котором наблюдается ГМА;
• оценка ДДЧ вида (4) FRD(r)i-1, соответствующая номеру фильтра с ГМА. Индекс ППИ r=ri-1 при этом полагается неизвестным.
Для определения дальности вида (1) от ФЦА до ПП, формирующей ГМА, излучается вторая пачка Рi с КНИ при крутизне ЛЧМ Si ≠ Si-1, по которой также определяются оценки НЗС τi по номеру дискрета с ГМА и соответствующей ДДЧ FRD(r)i. В работе рассматривается малоскоростной носитель РЛС. При малом интервале между пачками ΔtМП в бинарном пакете (Рi-1/Рi) фактически облучается одна и та же поверхность, ГМА формируется по сигналам от одной и той же ПП, т. е. ГМА не «дрейфует» по дискретам НЗС в ППИ и измерения/оценки НЗС τi-1 = τi = τ. Измерение/оценка ДДЧ вида (4) FRD(r)i≠FRD(r)i-1, что обусловлено отличием назначаемой крутизны Si ≠ Si-1 при одинаковой дальности до ПП, дающей ГМА. Аналогично известному способу измерения дальности и радиальной скорости для воздушной цели
, по указанным бинарным частотно-временным измерениям земли может быть определена и дальность Ri от ФЦА до ПП, формирующей ГМА и радиальная скорость ФЦА VR i по направлению этой наклонной дальности. При τi-1 = τi = τ для двух пачек, излучаемых при равных ППИ Tri = Tri-1 = Tr, обобщение известного метода и для решения задачи определения дальности от ФЦА до ПП приводит к следующим приближенным выражениям (без учета движения ФЦА на интервале между моментами излучения пачек импульсов):где int(.) – целая часть.
Угол наклона для этой дальности определяется выражением вида (2), в котором, например, при относительно ровной подстилающей поверхности используется геометрическая высота ФЦА, определяемая радиовысотомером. Радиальная скорость VRi ФЦА по направлению наклонной дальности (3)-(5), также по аналогии с известным способом , при заданной длине волны λ определяется приближенным соотношением:
Таким образом, при «бинарном» пакете из двух пачек импульсов с различной крутизной ЛЧМ, практически без использования данных инерциального канала МНС и независимо от уровня их ошибок, обеспечивается однозначное измерение наклонной дальности от ФЦА до определенной ПП с потенциальной точностью на уровне инструментальных ошибок измерения НЗС δτ / определения неоднозначной дальности δRНЗС=(c/2)δτ, а также радиальной скорости ФЦА по направлению этой наклонной дальности с потенциальной точностью на уровне инструментальной ошибки δFRD измерения ДДЧ / определения скорости (λ/2)δFRD). Очевидно, что автономность РЛ измерений на основе предлагаемого метода достигается «ценой» дополнительной пачки импульсов – в сравнении с традиционными «однопачечными» методами
, , . Но важно отметить, что при этом снимаются ограничения по углам наклона ГЛ, выдвигаемые при типовом АР управлении ГЛ , , , задаваемое направление ГЛ, в общем случае, может быть произвольным, включая и направленность ГЛ в окологоризонтное «свободное» воздушное пространство. В этом случае предложенный метод базируется на измерениях по ГМА, формируемых ПП в «следах» от БЛ и/или нижней части ГЛ и при этом нет необходимости в адаптивной режекции отражений по направлениям БЛ, реализуемой в типовых методах , , . Практически отпадает необходимость управления ГЛ при микронавигационных измерениях, поскольку суперпозиция сигналов от разных ПП при ЛЧМ уже не является негативным фактором, вносящим неоднозначность измерений. Как следствие, расширяются возможности совмещенного (одновременного) решения задач РЛ измерений траекторных параметров ФЦА относительно земли (в интересах микронавигации РЛС) и обнаружения/сопровождения воздушного объекта на фоне мешающих отражения от земли при КНИ, используя при этом прозрачные диапазоны ДДЧ между локальными (ЛМА) амплитудными максимумами и ГМА (см. рис. 3), которые формируются отражениями от земли на ДДЧ, соответствующих соотношению (4). Основные подходы к такой комбинации задач показаны в работах , , и в данной статье детально не рассматриваются. Отметим только, что вариации ППИ в рассматриваемом «бинарном» пакете ЛЧМ-пачек, осуществляемые при работе по воздушному объекту, не исключают возможность фоновой реализации предлагаемого метода РЛ измерений. Более того, при изменении ППИ, появляется возможность «дублирования» процедуры оценивания индекса ППИ для наклонных дальностей (например, на основе традиционной оценки целой части для отношения вида «изменение НЗС /приращение ППИ, вызвавшее это изменение НЗС» , , , но применительно к рассматриваемой ПП) для повышения достоверности оценки индекса ППИ.Точность оценки дальности вида (5) по бинарным ЛЧМ-сигналам зависит от ширины дискрета частоты (ширины фильтра) Δf= (1/nБПФTr), где nБПФ –количество импульсов в пачке (база быстрого преобразования Фурье) и от назначаемой комбинации значений крутизны ЛЧМ. Исходя из присущих РЛС ограничений по физической реализации ЛЧМ, значения крутизны Siи Si-1 назначаются таким образом, чтобы: с одной стороны, минимизировать ошибки определения дальности (5) и скорости (8); с другой стороны, в комбинации с назначаемым ППИ обеспечить «различимость» амплитудных максимумов (ГМА, ЛМА), формируемых в дискрете НЗС сигналами от двух ближайших ПП, дистанцированных кратно ППИ. Например, если реализуема только положительная крутизна, то для минимизации ошибок при определении (5) и (8) целесообразны значения крутизны, при которых |Si– Si-1|→max и | (Si/Si-1) |→min. Но при этом наименьшая крутизна при заданном ППИ должна обеспечивать достаточно широкий интервал ΔFRD(j/j-1)между ближайшими амплитудными максимумами на соответствующих ДДЧ вида (4):
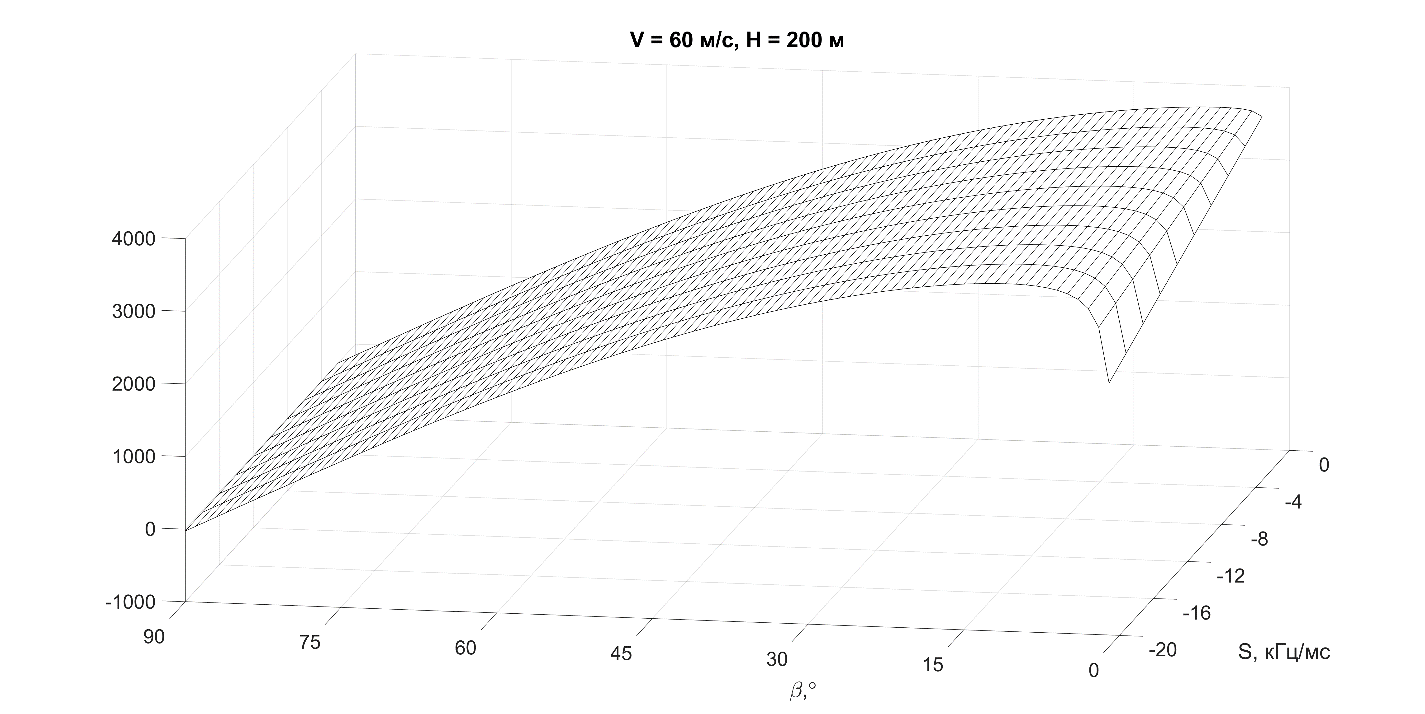
Рисунок 4 - Зависимость ДДЧ от угла наклона β к ПП и отрицательной крутизны ЛЧМ S
В условиях интенсивного маневрирования носителя РЛС возникает необходимость повышения информативности РЛ микронавигационных измерений при бинарных пачках импульсов при КНИ с ЛЧМ, прежде всего, обеспечивая измерение радиального ускорения ФЦА aR относительно земной поверхности (по направлению наклонной дальности до ПП в следе ГЛ или БЛ, дающей ГМА. Известны способы
, определения радиального ускорения воздушной цели относительно РЛС, реализуемые при КНИ с ЛЧМ. Можно показать, что их применение обобщается и для задачи определения радиального ускорения ФЦА aR относительно указанной ПП, но при этом требуется три пачки импульсов с различной крутизной ЛЧМ, что не позволяет использовать эти способы при рассматриваемых бинарных ЛЧМ-пачках и, следовательно, затрудняет совмещение сеанса РЛ микронавигационных измерений с «двухпачечным» шагом при решении РЛС вышеуказанных основных задач класса «воздух-воздух». Для обеспечения такой совместимости разработан нетрадиционный метод измерения aR при бинарных ЛЧМ-пачках, суть которого состоят в следующем.Рассмотрим выражение для ДДЧ, полученных по ЛЧМ-пачкам, излученным в (i-1)-ый и i-й моменты времени с интервалом между моментами излучения Δt. Предполагается, что присутствует ускорение aR, которой приводит в дополнительной ЛЧМ с крутизной Sa. Тогда
;
Учтем, что
,
.
Рассмотрим выражение для разности ДДЧ
из которого получаются соотношения
где f0 – несущая частота, Тозс = r Tr + τ – однозначная задержка сигнала от ПП, формирующей ГМА. Представим (11) в виде квадратного уравнения:
где ;
,
Отметим, что величины FRDi-1, ΔFRDi/i-1, Тозс i-1 измеряются, значения крутизны ЛЧМ, несущей частоты и интервала между моментами излучением ЛЧМ-пачек известны. Следовательно, значение крутизны Sa, обусловленной радиальным ускорением можно найти из решения квадратного уравнения (12) и далее по выражению (10) определяется радиальное ускорение ФЦА по направлению измеряемой наклонной дальности. Предложенный «квадратичный метод» определения радиального ускорения ФЦА при имитационном моделировании сложной траектории ФЦА типа «змейка» при интервале Δt = 0,25 с за время полета 350 с обеспечил среднее значение для ошибок оценивания ускорения ≈ 0,002 м/с2 при среднеквадратическом отклонении ≈ 1 м/с2.
3. Заключение
Таким образом, при типичном режиме КНИ бинарных ЛЧМ-пачек при вариациях крутизны ЛЧМ и ППИ, используемом на каждом цикле при решении известными адаптивно-робастными методами задач обнаружения, захвата, сопровождения воздушных целей на фоне земли и окологоризонтного свободного пространства, основываясь на частотно-временных измерений отражений от земли (традиционно рассматриваемых как «мешающие»), предложен информационно-автономный метод РЛ измерений микронавигационных параметров ФЦА радара, выполняемых одновременно с шагом решения в РЛС указанных основных задачи класса «воздух-воздух», обеспечивающий определение дальности, радиальных составляющих скорости и ускорения ФЦА по направлению к определенной ПП на облучаемой поверхности, формирующей наиболее интенсивный сигнал в спектре мешающих отражений, наблюдаемый в виде ГМА в ППИ. Метод не требует управления и специальной ориентации направления оси ГЛ для сеанса измерений, является независимым от информации МНС радара и, в сравнении с типичными методами РЛ измерений при КНИ, характеризуется повышенной информативностью, помехоустойчивостью и потенциальной точностью микронавигационных измерений, что обеспечивает возможность их эффективного использования в качестве данных корректирующего канала (датчика) в режиме РЛ-инерциальной микронавигации ФЦА, работоспособного и обеспечивающего приемлемую точность МНС при сложной радиопомеховой обстановке, исключающей возможность традиционного использования данных ГНСС.
