Многопараметрическая глобальная оптимизация при проектировании промышленного оборудования

Высокоточное моделирование в инженерном проектировании значительно снизило потребность в естественных испытаниях для проверки достигнутых характеристик проектируемого оборудования. С другой стороны, развитие инструментов проектирования привело к лавинообразному росту сложности требований к проектируемым моделям оборудования за счет увеличения числа оптимизируемых параметров и целевых характеристик. Узким местом задачи подбора параметров модели является сложность вычисления целевых характеристик по заданному набору параметров, что снижает возможность применения классических алгоритмов оптимизации, нацеленных на увеличение скорости работы алгоритмов и точности найденного решения, а не на сокращение количества проведенных испытаний при помощи вычислительной модели. В настоящее время для таких задач развитие получили многоуровневые алгоритмы оптимизации, которые на разных фазах поиска эксплуатируют модели разные по точности и по трудоемкости вычисления характеристик моделируемого оборудования – «грубые» модели позволяют сканировать пространство поиска с целью выявления перспективных областей и вариантов, а «качественные» модели используются для верификации и уточнения найденных решений. Научной проблемой, рассматриваемой в данной работе, является разработка многоуровневых методов оптимизации и схем их практической реализации для эффективного решения задач оптимизации проектных решений при проектировании высокотехнологичного промышленного оборудования.

В работе рассматриваются традиционные подходы к многопараметрической оптимизации применительно к задачам проектирования промышленного оборудования и делается упор на рассмотрении алгоритмов основанных на применении суррогатного моделирования, позволяющего сократить количество проведенных испытаний за счет частичного переноса исследования целевых характеристик от точной, но «медленной» вычислительной модели на «быструю» суррогатную модель, обеспечивающую выдачу значений с «погрешностью» неизвестной величины, но в то же время характеризующих динамику изменения целевых значений. Приводятся подходы, использующие предсказания от «коллектива» суррогатных моделей для выделения областей с наибольшим уровнем неопределенности, потенциально содержащих оптимальные решения.       

Результаты получены при финансовой поддержке исследования, реализуемого в рамках государственной программы федеральной территории «Сириус» «Научно-технологическое развитие федеральной территории «Сириус» (Соглашение № 18-03 от 10.09.2024) в соответствии с материалами работы «Алгоритмы многопараметрической глобальной оптимизации на основе суррогатных моделей для решения задач оптимизации проектных решений при проектировании промышленного оборудования».

Задача поиска наилучшего решения в зависимости от набора параметров широко распространена в сфере промышленного производства. Развитие средства имитационного моделирования, а также сквозных технологий создания суперкомпьютерных двойников и инженерного анализа позволяет в зависимости от того или иного сочетания исходных параметров получать оценки количественных целевых характеристик изделия. Формально задача подбора параметров ставится в терминах глобальной оптимизации, в которой требуется найти такое сочетание параметров, которое обеспечивает оптимум обобщенного критерия – представляемого в виде той или иной формы свёртки целевых характеристик. В результате такой формализации никакая информация о внутренней природе имитационной модели не раскрывается и её можно трактовать как «черный ящик» (некоторой вычислительной процедуры на вход которого подаются параметры, а на выходе наблюдается значение целевой функции, которое может быть недифференцируемым и сложными с вычислительной точки зрения)

Сложностью при разработке алгоритмов для проектирования промышленного оборудования является вычислительно-трудоемкость процедуры расчета функции цели и существенное число оптимизируемых параметров проектируемого объекта (например, всего одна итерация для расчета моделирования бокового порывистого ветра действующего на находящийся в воздухе объект занимает более 8300 процессорных часов (4 часа реального времени на 2016 ядрах)

При разработке алгоритмов оптимизации, учитывающих представленные особенности необходимо:

- применять техники, которые ограничивают количество замеров значений целевой функции;

- применять техники редуцирования пространства (например, при помощи методов редукции таких как PCA

- применять техники, обеспечивающие снижение количества трудоемких замеров целевой функции путем использования суррогатных моделей (например, Кригинг

Задача оптимизации для промышленного оборудования может быть поставлена как задача математического программирования в следующем виде: имеется набор из n параметров , необходимо подобрать такие значения параметров , что:

(1)

где D есть область возможных значений вектора параметров , а функции представляют параметры объекта, которые должны быть ограничены в искомом решении. Причем функции могут быть заданы как в явном виде, так и вычисляться в процессе расчета (для учета точек значения в которых не могут быть вычислены при помощи точной модели).

Можно выделить два основных подхода к решению задачи глобальной оптимизации с использованием суррогатного моделирования: многопараметрическая глобальная оптимизация с фиксированным множеством точек и адаптивная многопараметрическая глобальная оптимизация. Оба этих подхода могут применяться при исследовании промышленных моделей.

Подход с фиксированным множеством точек позволяет получить суррогатную модель пригодную как для поиска глобального оптимума, так и для других многопараметрических исследований на суррогатной модели, кроме того, упрощается переиспользование данных для повторных поисков и в целях машинного обучения при исследовании семейств моделей. При этом для такого подхода количество замеров будет больше, чем при использовании адаптивного итерационного подхода, нацеленного на уточнение только областей, потенциально содержащих глобальный оптимум, а не на построении суррогатной модели обладающей заданной точностью на всей области определения параметров. Алгоритм многопараметрической глобальной оптимизации на основе суррогатных моделей с фиксированным множеством точек работает с заданным заранее множеством точек или же с множеством точек заданной мощности, замеры в которых алгоритм может «заказать» однократно. Входными параметрами алгоритма являются:

- заранее сформированное множество точек пространства параметров и значения целевой функции в этих точках , где , либо количество точек ;

- функции ограничения ;

- коэффициент масштаба нормальных распределений  которые характеризуют распределение вероятностей отклонения от конкретного  в силу возможных погрешностей при изготовлении оборудования или в следствии естественного износа;

- параметр , определяющий количество точек, которые будут использованы для проверки потенциально оптимальных точек на условия связанные с возможным отклонением параметров при изготовлении оборудования или в следствии естественного износа. Проверочные вычисления будут производится на построенном суррогате и, хотя и могут быть достаточно трудоемкими, однако время вычислений будет несравнимо с временем вычисления значений функции в точке на точной модели. Значение параметра может быть выбрано в зависимости от характера изменения функции.

- признак возможности провести дополнительный замер при помощи точной модели в найденной точке

Проверочные вычисления будут производится на построенном суррогате и, хотя и могут быть достаточно трудоемкими, однако время вычислений будет несравнимо с временем вычисления значений функции в точке на точной модели. Количество точек может быть выбрано в зависимости от характера изменения функции, учитывая возможности провести дополнительный замер при помощи точной модели в найденной точке.

Алгоритм многопараметрической глобальной оптимизации на основе суррогатных моделей с фиксированным множеством точек можно представить в виде последовательности следующих шагов:

1. загружается изначальное заданное множество точек  где , либо же если изначальное множество точек не задано, то в результате одностадийной процедуры отбора точек формируется множество ;

2. проводится первоначальный отбор точек, из начального множества и исключаются точки с недопустимыми значениями. Формируется множество отобранных точек . Для каждой недопустимой точки X’ добавляется ограничение вида , где  – входной параметр масштаба;

3. строится суррогатная модель  на множестве точек . Для построения суррогатной модели может быть использован любой из существующих подходов, например, RBF, IDW, редукция Гауссовского процесса с различными ядрами, нейросетевой подход и т.д.;

4. определяется функция , где , которая задает для каждой точки множество проверочных точек, распределенных в соответствии с законами нормального распределения ;

5. решается задача нахождения глобального минимума , для функции . Поскольку все вычисления проводятся с использованием суррогатной модели на метод оптимизации не накладываются такие строгие требования по количеству замеров исследуемой функции;

6. найденная точка принимается в качестве искомого минимума. В случае наличия возможности провести дополнительный замер , найденная точка  оценивается при помощи точной модели и если точка допустимая, то среди всего множества точек  находится точка соответствующая минимальному значению .

Представленный выше алгоритм может быть модифицирован для автоматического выбора наилучшего способа построения суррогатной модели. Для этого Шаг 3 алгоритма заменяется следующую процедуру:

- часть точек (5%-10% от ) принимается в качестве множества тестовых точек  и исключается из множества , задавая таким образом множество ;

- строится множество суррогатных моделей , где  – количество рассматриваемых методов суррогатного моделирования, каждый индекс соответствует своему методу;

- решается задача нахождения индекса  соответствующего методу, который дает наименьшую суммарную ошибку  на тестовом множестве ,  такое, что . Метод суррогатного моделирования, соответствующий найденному решению, принимается в качестве основного и при помощи этого метода строится суррогатная модель  на всем множестве .

Для адаптивной многопараметрической глобальной оптимизации осуществляется одностадийный отбор точек. Суррогатная модель строится на равномерно распределенном множестве точек, что в среднем должно обеспечить одинаковую точность на всем множестве допустимых значений . Такое построение суррогатной модели имеет свои преимущества, однако в целях сокращения количества замеров выгоднее сосредоточить наибольшее количество замеров в местах потенциального минимума, именно такой подход обеспечивает адаптивный алгоритм многопараметрической оптимизации. Входными параметрами алгоритма являются:

- количество точек  которые могут быть заказаны алгоритмом;

- ограничения вида 

- коэффициент масштаба  нормальных распределений , которые характеризуют распределение вероятностей отклонения от конкретного  в силу возможных погрешностей при изготовлении оборудования или в следствии естественного износа;

- параметр  определяющий количество точек, которые будут использованы для проверки потенциально оптимальных точек на условия связанные с возможным отклонением параметров при изготовлении оборудования или в следствии естественного износа. Проверочные вычисления будут производится на построенном суррогате и, хотя и могут быть достаточно трудоемкими, однако время вычислений будет несравнимо с временем вычисления значений функции в точке на точной модели. Значение параметра  может быть выбрано в зависимости от характера изменения функции.

Основными шагами алгоритма являются:

1. формируется начальное множество равномерно распределенных точек, , где , в результате одностадийной процедуры отбора точек, описанной ранее;

2. определяется функция , где  которая задает для каждой точки множество проверочных точек, распределенных в соответствии с законами нормального распределения ;

3. проводится первоначальный отбор точек, из начального множества и исключаются точки с недопустимыми значениями. Формируется множество отобранных точек . Для каждой недопустимой точки  добавляется ограничение вида , где  входной параметр масштаба. Если , то алгоритм переходит на Шаг 7, иначе на Шаг 4;

4. строится суррогатная модель  на множестве точек . Для построения суррогатной модели может быть использован любой подход, который позволяет оценить не только значение в точке, но и меру неопределенности данного значения. В качестве такого подхода может быть выбрана редукция Гауссовского процесса с различными ядрами (например, RBF, Matern, RationalQuadratic и т.д,);

5. решается задача нахождения глобального максимума , для функции полезности  одним из методов, например из п.1 (различные возможные функции полезности будут рассмотрены далее) на суррогатной модели;

6. найденная точка передается для замера при помощи точной модели и формируется , после чего индекс  увеличивается на 1 и алгоритм переходит на Шаг 3;

7. на множестве точек  запускается процедура многопараметрической глобальной оптимизации на основе суррогатных моделей с фиксированным множеством с учетом изначально заданных и сформированных ограничений с возможностью точного замера в найденной точке.

Существует различные функций полезности , которые могут быть использованы в алгоритме. Рассмотрим следующие функции полезности, модифицированные для учета особенностей промышленного оборудования:

- модифицированная функция ожидаемого улучшения (функция EI'(X))

(2)

где,  – известный минимум,  – стандартное отклонение модели в точке , а  и  – функции распределения и плотности вероятности стандартного нормального распределения соответственно. Функция ожидаемого улучшения стремится выбрать точки, где возможно улучшение по сравнению с уже найденным экстремумом. Формально она вычисляет математическое ожидание улучшения целевой функции на следующем шаге и выбирает ту точку, где это ожидание максимально;

- модифицированная обобщенная функция ожидаемого улучшения (имеет обобщенную форму (3)), которая позволяет задать параметр , регулирующий исследовательскую и эксплуатационную стратегию, определяющий порядок рассматриваемого момента улучшения. Чем больше параметр , тем выше приоритет у исследовательской стратегии;

(3)

где  определяется рекурсивно для 

(4)

- модифицированная функция на основе производной функции моментов ожидаемого улучшения (5). Такой подход позволяет привязать к различным моментам ожидаемого улучшения веса, определяемые параметром

(5)

где .

Представленный выше алгоритм может быть модифицирован для автоматического выбора наилучшего ядра Гауссовского процесса при построении суррогатной модели. Для этого в Шаге 4 алгоритма необходимо предусмотреть возможностью использовать сразу несколько различных суррогатных моделей и выбирать наиболее подходящую

- взвешенное лучшее – на каждой итерации выбирается одна модель, которая вернула точку с наилучшем показателем выбранной функции полезности, умноженного на текущий вес данной модели. Начальное значение весов равно 1. Веса моделей в итерации при условии, что выбрана модель обновляются следующим образом:

(6)

- взвешенная комбинация – на каждой итерации выбирается точка с наилучшем показателем взвешенной линейной комбинации значений функций полезности для каждой суррогатной модели. Веса определяются нормализированным значением функции правдоподобия для каждой модели.

Для построения суррогатной модели при запуске алгоритма, когда еще нет никакой информации о поведении функции, необходимо задать множество точек пространства параметров. Одноэтапная выборка опирается на классическую конструкцию экспериментов и методы заполнения пространства. Идея классических экспериментов состоит в том, чтобы нивелировать влияние случайной ошибки на утверждение или отклонение гипотезы. К классическим методам относятся такие подходы, как методы полно-факторного анализа, Центрального композита, конструкции Бокса–Бенкена и Плакетта-Бурмана

- последовательность низкой расходимости Соболя

- последовательность низкой расходимости Халтона

- последовательность, полученная при помощи латинского гиперкуба

В качестве иллюстрации применения многопараметрической глобальной оптимизации на основе суррогатных моделей к проектированию промышленного оборудования рассмотрим задачу проектирования оборудования целевая функция которого описывается сложной функцией характерной особенностью которой является наличие «узкого ущелья» содержащего глобально-оптимальное решение и локального минимума расположенного в «широкой долине».

На рисунке 1 показано сравнение работы итерационного алгоритма, представленного в разделе 3 и алгоритма двойного отжига для первых 50 расчетов целевой функции. По оси y обозначен рекорд среднего значения окрестности среди точек, для которых был проведен расчет целевой функции. По оси x рассматривается количество данных точек. (рассматривается окрестность, так как для задачи проектирования промышленного оборудования значение целевой функции не должно сильно возрастать при смещении значений целевых параметров).

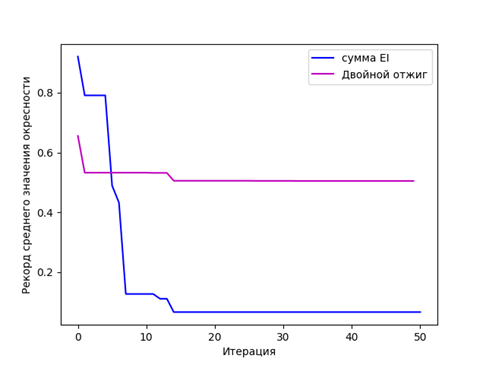
Рисунок 1 - Сравнение итерационного алгоритма и алгоритма двойного отжига

DOI:10.60797/IRJ.2025.151.35.1

Из графика видно, что итерационный алгоритм быстро приблизился к малому значению в то время, как двойному отжигу не хватило такого малого количество допустимых расчетов целевой функции для достижения значимого результата (если строить график для большего количества итераций решение, найденное двойным отжигом, будет не хуже). Таким образом, итерационный алгоритм может работать с функциями, которые требуют большого количества ресурсов для расчёта значений.

Таким же образом сравним результаты работы адаптивного алгоритм с модифицированным критерием EI c результатами работы алгоритма байесовской оптимизации (SEGO). График зависимости найденного рекорда функции сравнения показан на рисунке 2.

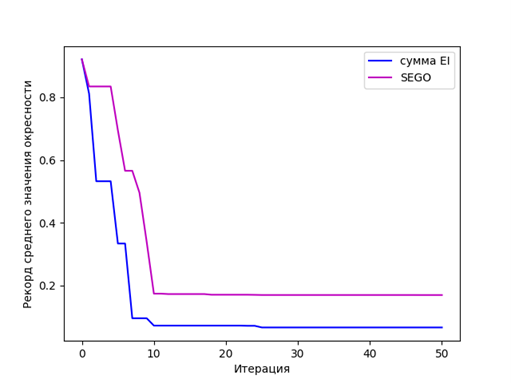
Рисунок 2 - Результаты сравнения работы адаптивного алгоритм с модифицированным критерием EI c SEGO

DOI:10.60797/IRJ.2025.151.35.2

Из графика видно, что, как и SEGO итерационному алгоритму понадобилось небольшое количество обращений к целевой функции для того, чтобы прийти к некоему результату, но результат, найденный SEGO имеет большее среднее значение в окрестности, чем результат, найденный итерационным алгоритмом. Такой результат можно объяснить тем, что алгоритм SEGO в основном заказывал дополнительные точки в области «ущелья» в то время как адаптивный алгоритм с модифицированным критерием EI ушел в «долину», имеющую более плавный ландшафт, что обеспечило ему в конечном счете преимущество с учетом требования по обеспечению устойчивости получаемого оптимального значения. Распределение запрошенных точек для каждого из алгоритмов показано на рисунках 3, 4.

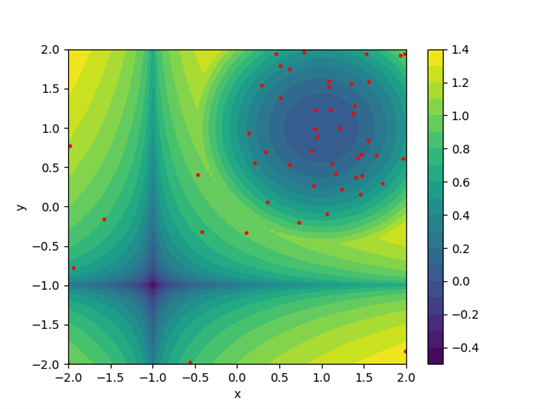
Рисунок 3 - Распределение точек итерационного алгоритма

DOI:10.60797/IRJ.2025.151.35.3

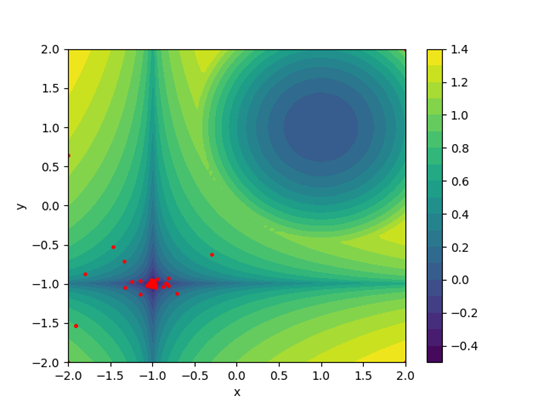
Рисунок 4 - Распределение точек SEGO

DOI:10.60797/IRJ.2025.151.35.4

В работе рассмотрены алгоритмы поиска глобально-оптимального решения применительно к задачам проектирования промышленного оборудования. Для задач проектирования промышленного оборудования выделены особенности определяющие подходы, которые могут быть использованы при решении подобных задач. В рамках приведенных подходов рассмотрены одностадийный и адаптивный алгоритмы многопараметрической глобальной оптимизации использующие суррогатные модели для сокращения количества трудоемких вычислений на точной модели. Для представленных алгоритмов приведены результаты тестирования.