Разработка модифицированного метода главных компонент для анализа биохимических изменений богатой тромбоцитами плазмы человека при ее хранении
Разработка модифицированного метода главных компонент для анализа биохимических изменений богатой тромбоцитами плазмы человека при ее хранении
Аннотация
Изучение биологических объектов с использованием современных математических методов анализа и классификации колебательных спектров представляет собой важный междисциплинарный аспект на стыке спектроскопии, биофизики и медицинских наук. В настоящей статье мы обращаем внимание на использование подобных методов на примере тромбоцитов и бактерий, представляющих сложные биологические объекты, для более глубокого понимания их устройства, свойств и потенциальных медицинских приложений. Цель данной работы заключается в исследовании и разработке модифицированного метода главных компонент для анализа биохимических изменений богатой тромбоцитами плазмы человека. В настоящей статье приведены результаты по разработке модифицированного статистического метода анализа для анализа изменений богатой тромбоцитами плазмы при ее хранении при температуре +5 °С в течение 6 недель.
1. Введение
Поскольку биофизические исследования в подавляющем большинстве случаев направлены на анализ сложных данных, для выделения спектральных изменений, в подавляющем большинстве случаев недостаточно базовой обработки спектрального сигнала. Группой применяемых методов в этом случае могут быть алгоритмы статистики и машинного обучения, используемые для решения задач классификации спектральных массивов. Полученные с помощью колебательной спектроскопии данные содержат много информации об атомах и молекулах в образцах. Будучи многомерными и, возможно, сильно коррелированными, данные часто являются сложными для анализа и интерпретации. Предварительная обработка данных часто требуется для удаления несущественных изменений в данных, таких как явления, вызванные рассеянием света, различиями в температуре или влажности. Традиционные методы анализа включают метод главных компонент (англ. Principal Component Analysis, PCA) , метод частичных наименьших квадратов (англ. Partial Least-Squares, PLS) и метод опорных векторов (англ. Support Vector Machine, SVM) . Существует множество вариаций, одной из наиболее распространенных моделей ML, используемой в биомедицине, является метод главных компонент – линейный дискриминантный анализ (PCA-LDA). PCA уменьшает размерность данных и устраняет некоторый шум; затем LDA изучает критерий, по которому можно разделить данные как принадлежащие к одному из нескольких классов, на основе обозначенных примеров. Важным аспектом того, насколько хорошо работает модель ML, является то, как она справляется с ранее невидимыми данными в клинических условиях: ее обобщаемость. Модель может просто запоминать данные, тем самым давая идеальную классификацию для данных, без возможности обобщения на невидимые данные. В идеале производительность должна быть протестирована с помощью недавно созданного набора данных. Однако существует много практических ограничений при сборе новых данных, особенно в клинических исследованиях, которые могут быть дорогостоящими и отнимать много времени. Анализ состояния тромбоцитов и бактерий с использованием комбинационного рассеяния света (КРС) представляет собой актуальное направление исследований в области медицины и биологии. КРС является мощным инструментом, который позволяет получать информацию о биохимическом составе клеток , структуре белков , липидов , нуклеиновых кислот и других молекул внутри клеток без их разрушения . В данном обзоре мы рассмотрим основные методы анализа состояний тромбоцитов и бактерий, методы дифференцирования и классификации , осуществляемые с помощью спектроскопии КРС для клеток крови человека и бактерий. Для анализа колебательных спектров в настоящее время широко применяют статистические методы и методы машинного обучения . Взаимосвязь между методами анализа состояния тромбоцитов и машинным обучением представляет собой актуальное направление в исследованиях биомедицинской диагностики, систем мониторинга здоровья и прогностической медицины . Машинное обучение (МО) может значительно улучшить точность анализа биомедицинских данных и помочь в прогнозировании состояний пациентов на основе информации, полученной из анализа тромбоцитов . Статистически обобщить эффективность традиционных моделей и моделей глубокого обучения между исследованиями было бы крайне трудно. На первый взгляд, модели глубокого обучения неизменно превосходят традиционные модели, иногда повышая точность всего на несколько процентов, но часто на значительную величину. Однако, учитывая методологические ограничения, а также склонность более сложных моделей чрезмерно приспосабливаться к данным, особенно к небольшим наборам данных, к этому наблюдению следует относиться с осторожностью. Следует также отметить, что модели глубокого обучения имеют больше гиперпараметров для использования, что может облегчить их перенастройку при выборе гиперпараметров.
В настоящей работе был разработан и апробирован модифицированный алгоритм для оценки изменений тромбоцитов при их хранении при температуре +5°С. Полученные данные могут быть полезны при создании методик транспортировки и хранения сыворотки и плазмы.
2. Методы и принципы исследования
Подготовка тромбоцитов была осуществлена следующим образом: образцы крови были взяты у одного здорового добровольца в количестве 30 штук в течение одного дня. Письменное информированное согласие было получено от здорового добровольца перед любыми процедурами исследования. Все документы исследования, включая информированное согласие и протокол, были одобрены Локальным этическим комитетом Независимости Балтийского федерального университета им. Иммануила Канта (Протокол № 8 от 16.05.2019). Здоровому добровольцу было 39 лет, он не имел острых и хронических заболеваний. Пациент не курил и не принимал никаких антиагрегантных или противовоспалительных препаратов. Свежие образцы венозной крови были взяты у здорового добровольца в вакуумную пробирку, содержащую ЭДТА (BD Vacutainer® spray-coated K2 EDTA Tubes). Ее центрифугировали при 60 g в течение 15 минут для последовательного отделения плазмы, богатой тромбоцитами (PRP), от эритроцитов (RBC) и лейкоцитов. После этого PRP собирали и помещали в новую пробирку. Тромбоциты окончательно собирали путем дальнейшего центрифугирования супернатанта при 1500 g в течение 15 мин. Все центрифугирования проводили при 4°C с использованием центрифуги Eppendorf 5702R. После подготовки тромбоцитов образцы помещались в лабораторный холодильник и хранились при температуре +5°С, а затем снимались каждый день, за исключением субботы и воскресенья в течение 6 недель с помощью поверхностно-усиленной рамановской спектроскопии (SERS). В процессе съемки снимались 30 спектров с пробы в день. Спектры сохранялись в формате .txt
Для обработки спектральных данных, был разработан модифицированный метод главных компонент на языке программирования Python с использованием следующих библиотек: а) NumPy: для работы с массивами и матрицами данных, б) Pandas: для загрузки и обработки данных из файлов Excel. в) Scikit-learn: для реализации алгоритма PCA Matplotlib: для построения графиков . Основной алгоритм работы программы был реализован с помощью основных этапов. Первым этапом являлась загрузка данных. В этом случае, код предполагает, что файлы с данными находятся в формате Excel (.xlsx) и хранятся по заданным путям в списке files. Цикл for file in files проходил по каждому файлу в списке. Вторым этапом была реализована предварительная обработка данных, в рамках которой осуществлялась коррекция базовой линии: Функция baseline_correction() применяла алгоритм коррекции базовой линии к каждому спектру в массиве данных. В данном случае использовался полиномиальная коррекция (метод «polynomial»), но можно было выбрать и другой метод, например, «rolling_mean» . Полиномиальная коррекция вычитала из каждого спектра аппроксимированный полиномиальный тренд, удаляя систематический шум и артефакты. Затем происходило удаление выбросов: Функция remove_outliers() должна удалить выбросы из данных. Функция должна удалять значения, которые значительно отличались от других значений в том же спектре. Функция apply_pca() применяла метод PCA к данным. Количеством главных компонент равно 2. pca.fit(data) обучала модель PCA на заданных данных. Затем происходило преобразование исходных данных в новое пространство с помощью PCA, сохраняя только 2 главных компоненты. После чего происходило вычисление дисперсии по каждой главной компоненте. Итоговым этапом было построение графика: plot_variance() строило график дисперсии главных компонент.
Таким образом, программный код выполнял следующие действия:
1. Загружал спектроскопические данные из файлов Excel.
2. Выполнял предварительную обработку данных, чтобы удалить шум и выбросы.
3. Применял PCA к очищенным данным.
4. Вычислял дисперсию по каждой главной компоненте.
5. Строил график дисперсии, чтобы визуализировать результаты анализа.
3. Основные результаты
Для исследования был применен метод главных компонент с целью снижения размерности данных, который преобразовывал набор данных с большим количеством признаков (переменных) в набор с меньшим количеством признаков, называемых главными компонентами. Главные компоненты являются линейными комбинациями исходных признаков, которые объясняют максимальную дисперсию данных. Были получены двумерные графики для двух главных компонент всех спектров, представленные ниже (см рис.1, рис.2, рис.3, рис.4).
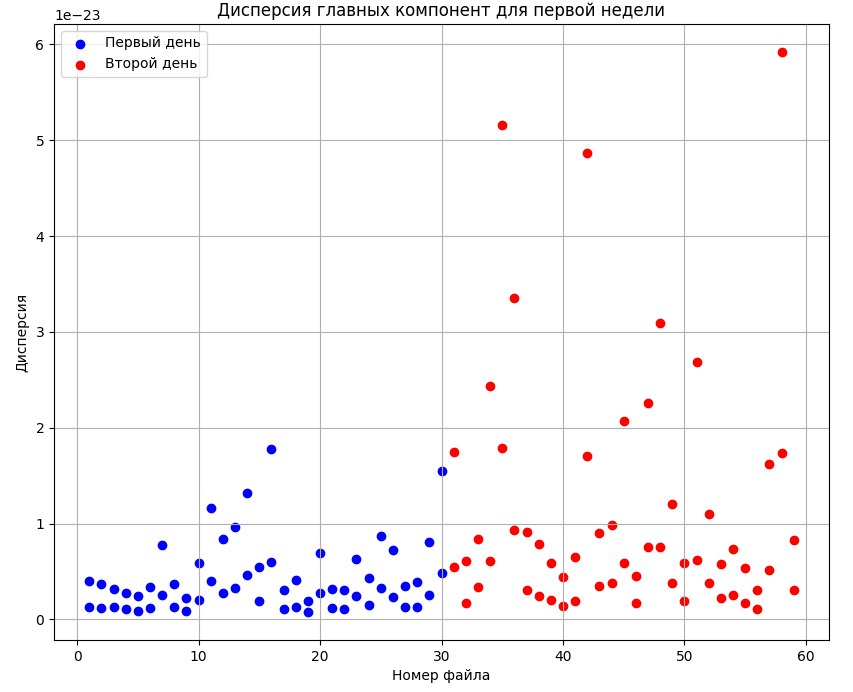
Рисунок 1 - Дисперсия главных компонент дней 1 и 2
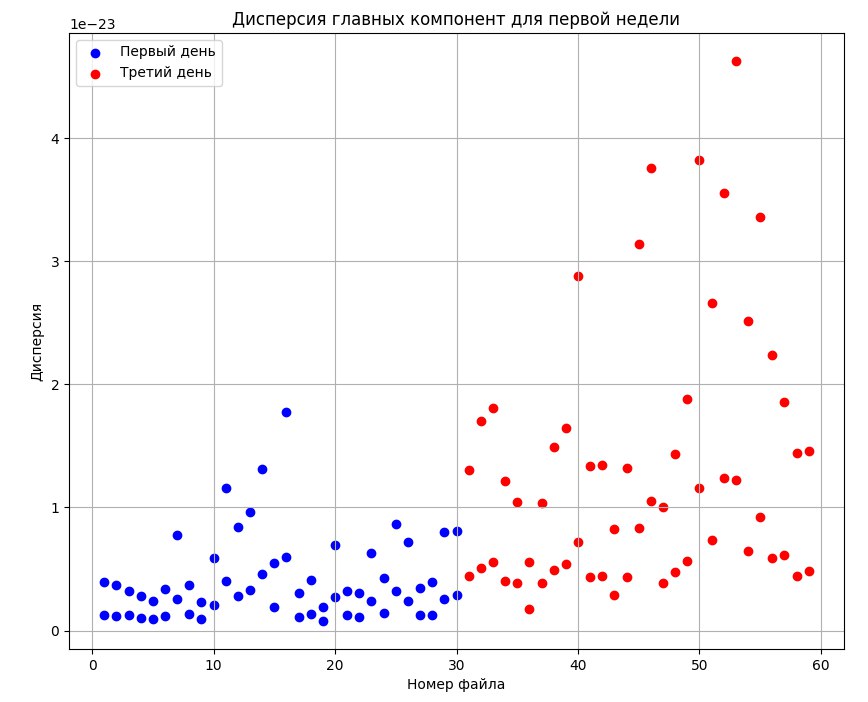
Рисунок 2 - Дисперсия главных компонент дней 1 и 3
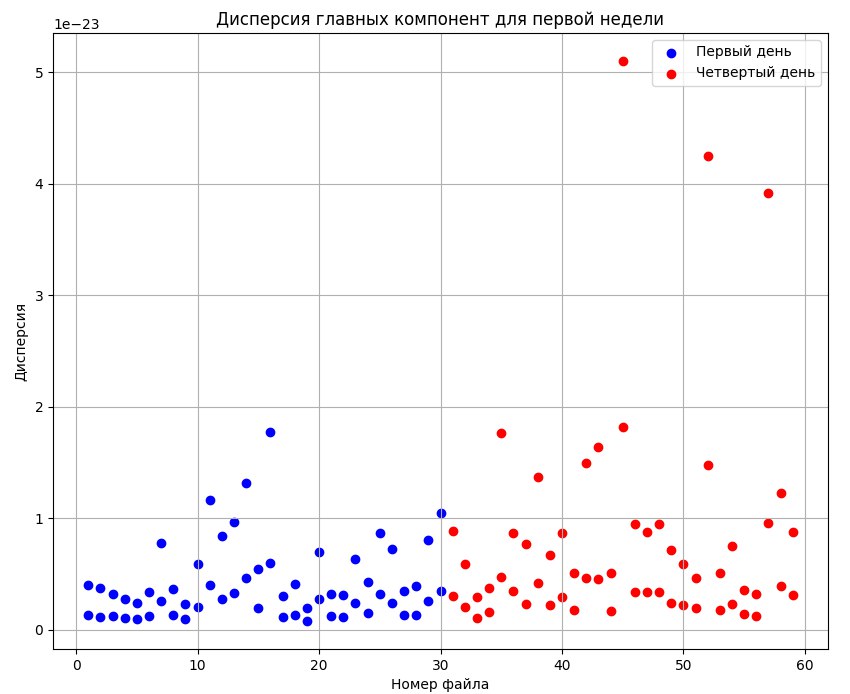
Рисунок 3 - Дисперсия главных компонент дней 1 и 4
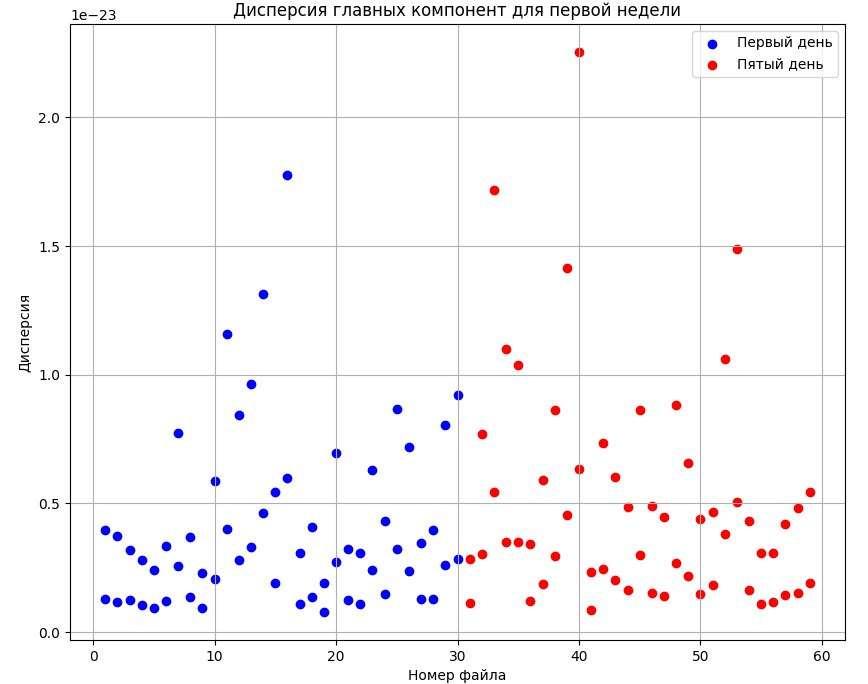
Рисунок 4 - Дисперсия главных компонент дней 1 и 5
4. Обсуждение
Была показана реализация программного алгоритма, который основывается на нескольких математических законах:
А. Ковариационная матрица: В этом случае данные представлены матрицей X (где строки – образцы, а столбцы – признаки), то ковариационная матрица C вычисляется как: C = (X - X̄)' * (X - X̄) / (N - 1), где X̄ – вектор средних значений признаков, N – количество образцов, а символ ' обозначает транспонирование матрицы.
Б. Собственные значения и собственные векторы:
В. Собственные значения и собственные векторы ковариационной матрицы C находят с помощью разложения C = Q Λ Q', где Q – матрица собственных векторов, а Λ – диагональная матрица собственных значений.
Г. Собственные векторы, соответствующие наибольшим собственным значениям, являются главными компонентами.
Д. Проекция на главные компоненты:
- данные X проецируются на пространство главных компонент W с помощью умножения на матрицу собственных векторов Q: W = X * Q.
Алгоритм был реализован на основе метода главных компонент. Математически он был направлен на поиск направлений максимальной дисперсии, стремясь найти новые оси (называемые главными компонентами), которые максимально объясняли бы вариативность данных. Эти оси являлись линейными комбинациями исходных признаков данных. Кроме того, метод главных компонент использовал ковариационную матрицу данных, которая показывала, как разные признаки связаны друг с другом. Проекция на главные компоненты же сводила размерность данных с именными, сохраняя максимальную дисперсию.
5. Заключение
В рамках проведенной работы была разработана программа, реализующая модифицированный метод главных компонент, который успешно дифференцировал состояние тромбоцитов в зависимости от условий хранения. Он представляет собой перспективный инструмент для анализа биохимических изменений в богатой тромбоцитами плазме и может внести вклад в развитие методов оценки качества богатой тромбоцитами плазмы при ее хранении. Работа алгоритма метода позволяет определить наличие биохимических изменений, развивающихся по мере хранения образцов. Полученные результаты позволяют глубже понять процессы деградации богатой тромбоцитами плазмы и могут быть использованы для оптимизации условий хранения и транспортировки богатой тромбоцитами плазмы, что имеет важное значение для медицины и биофизики. Алгоритм может быть использован исследователями для оценки изменений и других биологических объектов.
