ОПТИМИЗАЦИЯ АЭРОДИНАМИЧЕСКОГО ПРОФИЛЯ ВЕТРЯНОЙ ТУРБИНЫ МЕТОДОМ ПАРАМЕТРИЧЕСКОГО МОДЕЛИРОВАНИЯ
ОПТИМИЗАЦИЯ АЭРОДИНАМИЧЕСКОГО ПРОФИЛЯ ВЕТРЯНОЙ ТУРБИНЫ МЕТОДОМ ПАРАМЕТРИЧЕСКОГО МОДЕЛИРОВАНИЯ
Аннотация
Статья посвящена научным исследованиям, направленным на развитие современных подходов к изучению общих свойств и принципов работы вертикально-осевых ветроэлектростанций, которые отвечают современным потребностям в обеспечении электроэнергией спасательных формирований в зоне чрезвычайных ситуаций. Научной новизной исследования является системный методический подход к разработке ветряной турбины, устанавливающий функциональные связи между конструктивными параметрами лопаток турбины и ее энергетическими характеристиками. В качестве методологической основы был использован метод параметрического моделирования для выявления взаимосвязей исследуемого объекта с взаимодействующими факторами, такими как координаты аэродинамического профиля и зоны отрыва потока, угол атаки и коэффициент лобового сопротивления. Конечные аэродинамические профили показали значительные улучшения по сравнению с исходными базовыми формами.
1. Введение
В результате растущего интереса к экологически чистым и возобновляемым источникам энергии, в последние годы энергия ветра стала одним из наиболее развитых и используемых источников энергии. Для получения максимальной производительности энергии ветра используются ветряные турбины. К настоящему времени проведено и проводится множество исследований по этим турбинам . Оптимизация формы профиля является главным этапом проектирования аэродинамических компонентов, таких как лопасти ветряных турбин . Процесс оптимизации профиля обычно включает в себя три основных компонента: параметризацию формы, оценку профиля и оптимизацию. Среди них метод параметризации определяет как пространство проектирования, так и сложность задачи оптимизации. Чтобы обеспечить эффективность, метод параметризации должен охватывать широкое пространство проектирования, используя незначительное количество проектных параметров. Это особенно важно на начальном этапе проектирования, когда накладываются минимальные геометрические ограничения, и имеется возможность внесения существенных изменений профиля в процессе оптимизации.
2. Методы и принципы исследования
По мере расширения геометрической области применения каждого параметра появляются классические подходы, основанные на изгибах контурных линий или контрольных точек. Например, популярный метод параметрического сечения (PARSEC) использует множество параметров для представления основных характеристик профиля, включая радиусы передней кромки и расположение верхнего и нижнего крыла, и строит поверхность профиля с использованием полинома шестого порядка. Другим популярным методом является параметризация Безье , которая строит верхнюю и нижнюю поверхности аэродинамического профиля с помощью кривых Безье, определенных заранее выбранными контрольными точками. Одной из основных проблем, связанных с вышеупомянутыми методами, является их неспособность или неэффективность включать функции высокой точности; эти методы имеют фиксированное число параметров и ограниченный диапазон точности, в то время как параметризация Безье требует кривых Безье более высокой степени для описания сложных форм, которые неэффективны для вычисления .
Для рассмотрения более мелких деталей аэродинамических профилей или, что эквивалентно, для представления более сложных кривых можно использовать либо B-сплайны , которые создают кривые путем соединения низших порядков сегментов Безье, определенные контрольными точками. По мере увеличения числа контрольных точек, эти методы перемещаются на локальный конец спектра и становятся способными отображать объекты с высокой точностью, но вычислительная сложность процесса также увеличивается.
Одним из способов уменьшить количество проектных параметров является группировка контрольных точек таким образом, чтобы в качестве параметров можно было использовать глобальные преобразования, такие как скручивание и утолщение. Этот метод известен как деформация свободной формы (FFD) . Аналогичный метод, называемый подходом к элементам домена с использованием радиальной базисной функции (RBF) , также существует и использует RBF для придания деформации профилю.
Ближе к глобальному концу спектра можно отметить методы, использующие спектральное построение базисных функций для формирования или деформации профилей. Одним из популярных вариантов базисных функций являются доминирующие режимы из разложения по сингулярным значениям (SVD) набора данных профиля. Другие варианты включают синусоидальные функции подхода Хикса-Хенне , которые создают «неровности» на эталонной поверхности профиля, и поверхностные функции метода преобразования функций класса/формы, которые представлены в виде произведения функции класса и функции формы, полученной линейной комбинацией многочленов Бернштейна. Тем не менее эти методы также имеют зависимость от размерности, заключающуюся в том, что всегда требуется больше базовых функций или режимов, чтобы они выдавали функции высокой точности.
В работе была применена генеративная сеть (GAN) для изучения основных вариаций формы базы данных профиля и использования их для параметризации форм, сохраняя при этом высокоточные характеристики за счет дополнительного шумового пространства. Однако, как и во многие других методах, при уменьшении размеров оптимальный профиль лопасти находится вблизи базы данных, что не всегда верно.
3. Основные результаты
В данной работе был использован метод параметрического моделирования DBD designer для решения задачи по оптимизации аэродинамического профиля ветротурбины. Метод DBD – это новая и универсальная это система визуального проектирования баз данных, которая преобразует существующие формы и способна интерполировать пространство объекта, обеспечивая как высокоточное представление форм без учета размерности, так и радикальные модификации форм без каких-либо неявных геометрических ограничений. Оптимизация начинается с выбора форм базовой линии, а затем выполняется оценка и оптимизация аэродинамических профилей, сформированных путем изменения этих базовых форм с помощью DBD. DBD designer не основан на конкретном инструменте оценки аэродинамического профиля или конкретном оптимизаторе. Для повышения эффективности и согласованности был использован XFOIL для получения данных о производительности. Обработка и повторная загрузка измененных координат профиля производилась индивидуально в конце каждого алгоритма DBD, преобразующего координаты вихревых зон с относительно более высокой концентрацией в местах со значительной кривизной лопасти. В качестве результатов этих расчетов представлен профиль, показанный на рисунке 1.
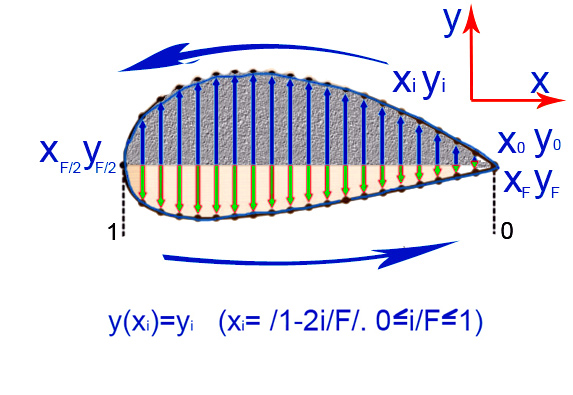
Рисунок 1 - Форма аэродинамического профиля и координаты базовых фигур
Применив метод DBD для восстановления базы данных, мы обнаружили, что основная часть профилей всей базы данных были восстановлены с ошибкой MAE <1%. Даже для двух профилей с наибольшей погрешностью оптимизация DBD все равно привела к ошибке MAE менее 1,5%. На рисунке 2 показан процент профилей, которые были оптимизированы с допуском 0,5% ошибки MAE, по отношению к общему числу профилей.
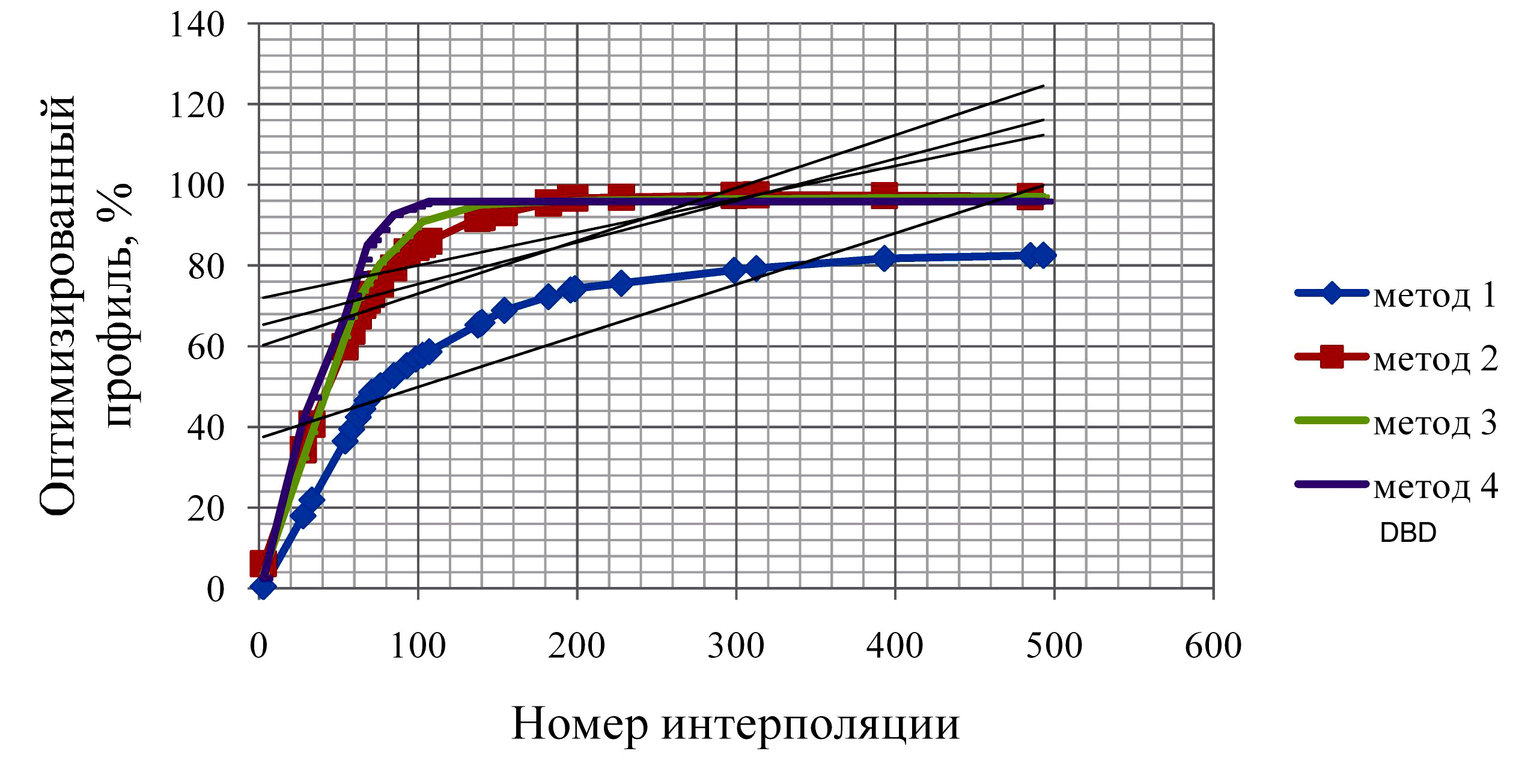
Рисунок 2 - Зависимость профилей, восстановленных с допуском MAE
4. Заключение
В данной работе был использован метод параметрического моделирования DBD designer для решения задачи по оптимизации аэродинамического профиля ветротурбины. Применение DBD моделирования для оптимизации формы аэродинамического профиля в 2D, показало его точную реконструкцию в существующей базе данных аэродинамических профилей и позволило провести радикальные изменение формы аэродинамического профиля без использования геометрических ограничений путем интерполяции пространства проектирования. Установлено, что функция экстраполяции DBD значительно способствует повышению производительности метода, при этом метод DBD сходится быстрее, чем любые другие традиционные подходы.
