ПРОЕКТИРОВАНИЕ ШАБЛОНА С++ ДЛЯ ПОСТРОЕНИЯ РЕШАЮЩИХ ГРАФОВ В ПРОДУКЦИОННЫХ СИСТЕМАХ
ПРОЕКТИРОВАНИЕ ШАБЛОНА С++ ДЛЯ ПОСТРОЕНИЯ РЕШАЮЩИХ ГРАФОВ В ПРОДУКЦИОННЫХ СИСТЕМАХ
Научная статья
Московский государственный технический университет им. Н.Э. Баумана, Россия, Москва
* Корреспондирующий автор (z.n.rusakova[at]mail.ru)
АннотацияВ связи с внедрением систем искусственного интеллекта (ИИ) актуальной задачей является повышение эффективности систем логического вывода. Рассматривается проектирование шаблона С++ для построения решающих графов в продукционных системах ИИ. Описывается разработанный класс С++, реализующий обратный вывод на графах И-ИЛИ. Выбранная платформа С++ позволяет повысить эффективность решения за счет увеличения быстродействия и распараллеливания вычислений и использовать в системах реального времени.
Ключевые слова: списки, поиск, деревья, шаблоны, классы, правила продукции, динамические структуры, логический вывод.
DESIGNING A C++ TEMPLATE FOR CONSTRUCTING DECISION GRAPHS IN PRODUCTION SYSTEMS
Research article
Rusakova Z.N.*
Bauman Moscow State Technical University, Russia, Moscow
* Corresponding author (z.n.rusakova[at]mail.ru)
AbstractIn connection with the introduction of artificial intelligence (AI) systems, increasing the efficiency of logical inference systems is an urgent task. The current article examines designing a c++ template for constructing decision graphs in production systems as well as introduces and describes a C++ class that implements reverse inference on and-or graphs. The chosen C++ platform makes it possible to increase the efficiency of the solution by increasing the speed and parallelization of calculations and using them in real-time systems.
Keywords: lists, search, trees, templates, classes, product rules, dynamic structures, logical inference.
Введение
Большинство существующих инструментальных оболочек продукционных систем ИИ разработаны на языках высокого уровня. К ним относятся такие системы как Clisp, Prolog, Nexpert Object, Jess [1], [2], [3]. В большинстве систем используется прямой логический вывод, вызывающий проблему разрешения конфликтного набора правил. Диалоговый режим выполнения затрудняет использование систем в режиме реального времени.
Целью данной работы является разработка программного инструментария обратного логического вывода для продукционных систем, описываемых графами И-ИЛИ и предназначенных для использования в режиме реального времени. В статье рассматривается проектирование шаблона С++ для построения деревьев решения на графах И-ИЛИ, в котором реализован обратный вывод на основе метода поиска в глубину. Использование платформы С++ позволяет повысить быстродействие и распараллелить процедуру вычислений Построение решающего графа выполняется без запросов данных в автоматическом режиме и позволяет интегрировать механизм вывода с базами данных.
Организация приложения ИИ в виде системы продукций обладает важными преимуществами: правила не вызывают друг друга, все управление правилами вынесено в стратегию управления, между правилами нет прямой связи по данным, все данные находятся в рабочей памяти [1], [5], [10].
Посылка правила является множеством условий, связанных логической связкой «И» «. Семантические определения вершин задается в словаре, в котором каждой вершине ставится в соответствие понятие предметной области. Правила базы знаний формулируются в терминах понятий предметной области. В качестве формальной модели описания продукционной базы (или базы правил) используется представление графом И-ИЛИ [2], [3]. Правила продукции представляются модулем с двумя типами вершин: Первый тип - конъюнктивные вершины - входные вершины, соответствующие условиям правила, и выходная вершина, соответствующая заключению правила. При их графическом отображении используется обычное представление вершин - маленькая окружность. Второй тип вершин - вершина, соответствующая имени или номеру правила. Для их представления используется маленький квадратик. Логический вывод (решатель, или интерпретатор) в продукционных системах соответствует поиску решений в И-ИЛИ графах. Существуют две основные стратегии вывода на множестве правил-продукций: прямой и обратный вывод. Решающий граф определяется как подграф из разрешимых вершин, представляющих имена правил.
Алгоритм решения
Основные структуры данных. Вершина описывается классом Ver, полями которого объявляются целые числа – номер вершины (int num) и поле flag, определяющее выбор вершины в процессе поиска - выбрана, доказана, запрещена. Для описания конъюнктивных входных вершин модуля описывается класс Mas Ver. Полями класса объявляются: количество вершин (int n) и указатель на динамический массив вершин - Ver* b.
Модуль правила описывается классом Modul_prav, включающим следующие поля: номер правила - int num_p, выходная вершина модуля -Ver vc, массив входных вершин Ver * mv, количество - int n, и флаг просмотра - int metka. Множество правил базы знаний описывается списком модулей правил. Вершина – открытая, пока не порождены ее потомки [1], [8]. Эти вершины составляют фронт вершин, являющихся потомками вершины раскрытия. Вершина –закрытая, если в процессе поиска порождены все ее потомки. Вершины хранятся и обрабатываются в двух списках: список открытых вершин и список закрытых вершин. Вершины графа в процессе поиска из списка открытых переписываются в список закрытых. В стратегии поиска в глубину используется механизм стека: вершина для раскрытия выбирается из головы списка открытых вершин, потомки записываются в голову. В отличии от поиска в пространстве состояний в графах И-ИЛИ [1], [6] необходимо в процессе решения формировать не только списки открытых и закрытых вершин, но списки правил, которые определяют дерево решения.
Для решения задачи моделирования средствами обобщенного программирования C++ разработан класс Poisk_graf_I_ILI. Полями класса Poisk_graf_I_ILI объявляются списки открытых и закрытых вершин и правил, список базы правил, описывающих граф, флаги решения, определяющие результат поиска. Параметрами шаблона являются классы, описывающие правила графа и вершины.
В конструктор класса с параметрами передаются аргументы: список правил графа, целевая вершина и массив заданных вершин. В конструкторе класса вызываются конструкторы создания списков открытых и закрытых вершин и выполняется их инициализация.
template < class T , class Tr > // t - Modul_prav, Tr - Ver
class Poisk_graf_I_ILI {
public:
int flagys, flagnot, flag_poisk; // флаги решения
Tr cel, *dat ; // вершины- цель и исходные данные
Tr vt ; // Ver
int nd; // число заданных вершин - исходные данные
// списки открытых и закрытых вершин и правил
List <Tr> listOpenNodes;
List <Tr> listCloseNodes;
List <Tr> listZapretNodes;
List <T> listOpen_prav;
List <T> listClose_prav;
List <T> listZapret_prav;
List <T> baza; // список правил графа
//Конструкторы и методы класса
}’;
Для моделирования списков используется разработанный шаблонный класс List [4], [7], [8], [9]. В конструкторе инициализируется список правил – baza, в список закрытых вершин lstCloseNodes записываются заданные вершины, целевая - помещается в голову списка открытых вершин listOpenNodes, задаются флаги решения flagys=1, flagnot=1; flag_poisk=0;
Список закрытых вершин и правил являются рабочей памятью, формируемой в процессе поиска. Список закрытых правил содержит решающий граф. В алгоритме поиска в глубину вершина раскрытия выбирается из головы списка открытых вершин. В графах И-ИЛИ потомки - это конъюнктивные вершины правила, раскрывающие текущую подцель и не входящие в список закрытых, т.е. доказанных. По принципу формирования стека все входные вершины модуля правила, не входящие в список закрытых вершин, записываются в голову списка открытых вершин, а выбранное правило записывается в голову открытого списка правил. Определение потомков подцели, связанных связкой конъюнкции, и формирование списков открытых вершин и правил выполняется в методе potomki_I_ILI_gl () по следующему алгоритму.
Из головы списка открытых вершин выбирается текущая подцель. Выбранная вершина является образцом для поиска в базе правил первого правила, для которого выполняются условия: правило еще не выбиралось (метка правила равна 0), правило не находится в списке запрещенных, вершина, соответствующая заключению правила (выход правила продукции), равна текущей подцели. Поиск выполняется в цикле «пока»:
Пока не конец базы правил и не нашли правила (flag=1) выполняется поиск по образцу. Если рассмотренные условия выполняются, то метка правила устанавливается в 1, флаги поиска сбрасываются: flag_poisk=0; flag=0. Выбранное правило записывается в голову открытого списка правил.
Следующая задача - запись потомков в голову списка открытых вершин. Для этой цели определяется покрытие входных вершин множеством вершин рабочей памяти из списка закрытых вершин. Определяется число известных входов и установка флага в 1 для вершин, входящих в рабочую память: в цикле выполняется проверка вхождения каждой вершины из входов модуля – (m число входов) в список закрытых вершин, во вложенным цикле проверяется условие вхождения каждой вершины из входов модуля - в список закрытых вершин, если входит флаг вершины устанавливается в 1 – вершина закрыта=1.
Если число доказанных входных вершин правила меньше числа входов правила, то остальные вершины, не входящие в рабочую память, записываются в голову списка открытых вершин и будут раскрываться на следующих шагах поиска. Все недоказанные вершины пишем в голову списка открытых вершин, проверяя поле у вершины (flag=1 or flag=0 1), если входят в заданные. Если число входных вершин модуля равно число вершин, входящих в список закрытых вершин, т.е. покрываются этим множеством - то модуль доказан и новых подцелей на данном шаге нет.
Для выходной вершины модуля флаг устанавливается в 1, что означает вершина доказана и модуль выполнен Если эта вершина равна целевой вершине, то решение получено, устанавливается флаг решения flagys=0 и выполняется выход из цикла просмотра базы правил. Правила, для которых входы доказаны, должны быть удалены из открытого списка правил и записаны в закрытый список правил. Подцель, соответствующая этой вершине, должна быть переписана в список закрытых вершин, ее флаг просмотра устанавливается в 1.
Если решение не достигнуто, необходимо возвращаться по ветви поиска для проверки предыдущих правил из списка открытых правил, доказывать их выполнение и раскрывать вершины подцелей из списка открытых вершин, т.е. доказывать истинность вершин правил предков. Назовем эту процедуру разметкой правил. Для ее реализации разработан метод класса – razmetka(). Этот метод вызывается из метода поиска потомков.
Код метода:
int potomki_I_ILI_gl () { int i,j, k, l ,m, ip,flag, flag_poisk_pr; flag=1; flag_poisk_pr=1; baza.cur=baza .first; while ( baza.cur && flag==1 ) { //цикл по базе правил // поиск по образцу – выбор правила if ( listOpenNodes.first->data == baza.cur->data.vc && baza.cur->data.metka ==0 && (baza.cur->data.metka !=-1)) { baza.cur->data.metka=1; //метка правила m=baza.cur->data.n; //число входов правила flag_poisk_pr=0; flag=0; // нашли правило // в цикле определяется число не известных входов и установка флага for( i=0,k=0; i<m; i++) { // цикл по списку закрытых вершин listCloseNodes.cur=listCloseNodes.first; //начало списка while(listCloseNodes.cur !=0) { if (listCloseNodes.cur->data == baza.cur->data.mv[i]) { k++; //флаг вершины ставим в 1 baza.cur->data.mv[i].flag=1; break; } // вершину нашли и вышли listCloseNodes.cur=listCloseNodes.cur->next; } } // end for // запись правила в список открытых вершин listOpen_prav.add_head(baza.cur->data); // потомки - вершины И правила в список отрытых for(i=0,l=0; i<m; i++) if( baza.cur->data.mv[i].flag == 0){ l++; listOpenNodes.add_head( baza.cur->data.mv[i] ); } if (l==0) razmetka();// вызов метода } baza.cur = baza.cur->next; // переход по базе правил } return flag_poisk_pr; }Организация построения дерева решения методом поиска в глубину от цели выполняется в методе poisk_I_ILI_gl() по следующему алгоритму.
Пока список открытых вершин не пуст или целевая вершина не достигнута на каждом шаге цикла выполнить:
Вызвать метод flag_poisk = potomki_I_ILI_gl();
Если нашли решение, то вывод решающего графа,
иначе если не нашли правила для вершины подцели, и в открытом списке правил осталось одно правило, то решения нет,
иначе вызов метода возврата (бэктрекинга).
В методе возврата правило и подцели, соответствующие нераскрытым вершинам удаляемого правила, текущая подцель из головы списков открытых правил удаляются и записываются в списки запрещенных вершин и правил. Код метода:
void poisk_I_ILI_gl() {
while ( flagys && flagnot ) {
flag_poisk = potomki_I_ILI_gl();
if ( flagys==0) //вывод списка закрытых правил
listClose_prav .print_List();
else
if ( flag_poisk && listOpen_prav.first->next==0 )
flagnot=0; // не решения
else
vozvrat();// вызов метода бэктрекинга
}
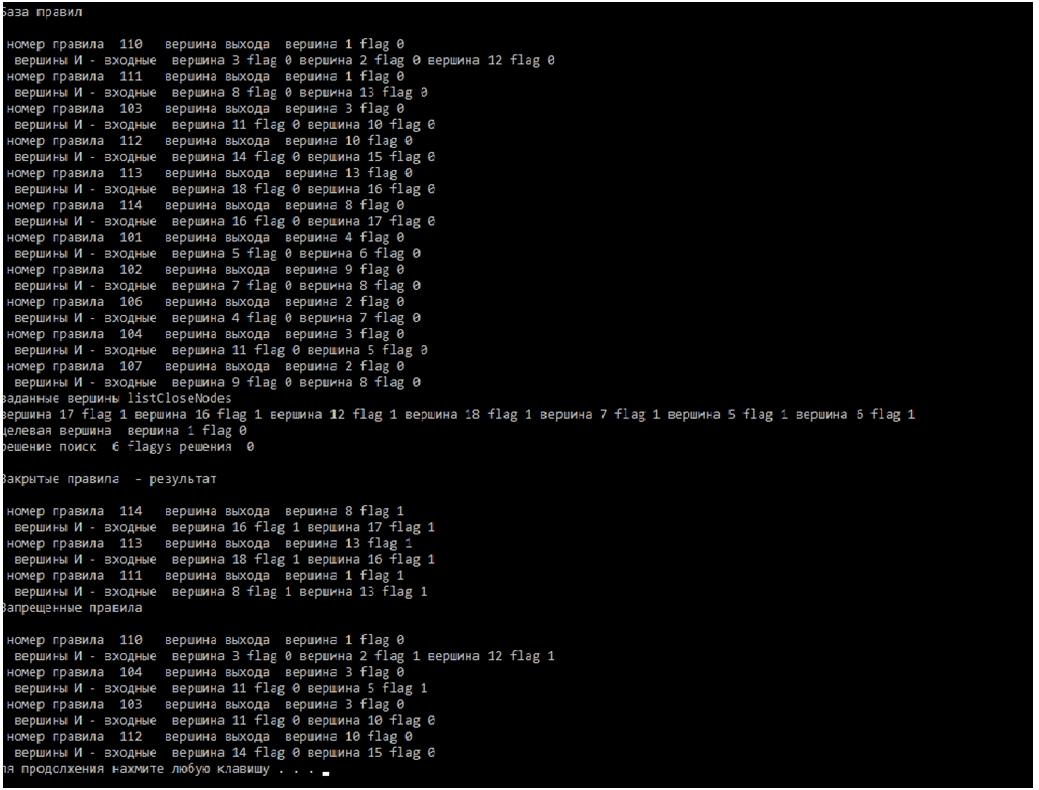
Результаты тестирования решателя приведены ниже. Для теста используется вышеописанное формализованное представление продукционной базы правил. Конкретное наполнение определяется в словаре. Выводятся следующие данные: фрагмент базы правил – для каждого правила выводится номер правила, выходная вершина, список входных вершин, флаги вершин по умолчанию в нуле. Выводятся список заданных вершин и целевая вершина. Результат работы: список закрытых правил, который содержит граф решения, список запрещенных вершин и правил, полученных в результате поиска.
Рис. 1 – Результаты тестирования решателя
ЗаключениеОписывается обобщенный класс С++, реализующий обратный логический вывод в продукционных системах ИИ, описываемых графами И-ИЛИ. Программный инструментарий является основой для разработки полиморфной иерархии классов, использующих коллекцию различных методов поиска для композиции результатов.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Новиков Ф.А. Символический искусственный интеллект: математические основы представления знаний / Ф.А. Новиков. Москва: Издательство Юрайт, 2019,278
- CLIPS: A Tool for Building Expert Systems. — [Electronic resource]. URL: http://www.ghgcorp.com/clips/CLIPS.html (accessed 23.10.2001)
- Jess, the Expert System Shell for the Java Platform. — [Electronic resource]. URL: http://herzberg.ca.sandia.gov/jess/main.html (accessed 23.10.2001)
- Седжвик Р. Алгоритмы на C++. Фундаментальные алгоритмы и структуры данных / Р. Седжвик. – М.: Вильямс, 2013. – 1056 с.
- Кормен Т. Алгоритмы: построение и анализ, 3-е изд / Т. Кормен, Ч. Лейзерсон, Р. Ривест и др. – М.: Вильямс, 2013. – 1328 с.
- Страуструп Б. Язык программирования C++ / Б. Страуструп. СПб.: Бином, 1999. c. 990.
- Русакова З.Н. Поиск решений в продукционных системах методами обобщенного программирования / З.Н. Русакова // Международный научно-исследовательский журнал № 2 (104). 2021 Часть 1. Февраль.
- Русакова З.Н. Динамические структуры данных и вычислительные алгоритмы Visual C++ / З.Н. Русакова. Санкт-Петербург.2014, 272 с.
- Русакова З.Н. Структуры данных в С++ / З.Н. Русакова, И.В. Рудаков. Москва: Издательство МГТУ им. Н.Э Баумана.2020, c157.
- Русакова З.Н., Разработка инструментальных средств для решения задач принятия решений / З.Н. Русакова // Интеллектуальные системы. Труды Девятого международного симпозиума, М., РУСАКИ, 2010, 773.
Список литературы на английском языке / References in English
- Novikov F.A. Simvolicheskij iskusstvennyj intellekt: matematicheskie osnovy predstavlenija znanij [Symbolic artificial intelligence: mathematical foundations of knowledge representation] / F.A. Novikov. Moscow: Yurayt Publishing House, 2019, 278. [in Russian]
- CLIPS: A Tool for Building Expert Systems. — [Electronic resource]. URL: http://www.ghgcorp.com/clips/CLIPS.html (accessed 23.10.2001)
- Jess, the Expert System Shell for the Java Platform. — [Electronic resource]. URL: http://herzberg.ca.sandia.gov/jess/main.html (accessed 23.10.2001)
- Sedgwick R. Algoritmy na C++. Fundamental'nye algoritmy i struktury dannyh [Algorithms in C++. Fundamental algorithms and data structures] / R. Sedgwick. - M.: Williams, 2013– - 1056 p. [in Russian]
- Kormen T. Algoritmy: postroenie i analiz [Algorithms: construction and analysis], 3rd ed. / T. Kormen, Ch. Leiserson, R. Rivest et al. - M.: Williams, 2013. - 1328 p. [in Russian]
- Stroustrup B. Jazyk programmirovanija C++. [Programming language C++] / B. Stroustrup. St. Petersburg: Binom, 1999. p. 990. [in Russian]
- Rusakova Z.N. Poisk reshenij v produkcionnyh sistemah metodami obobshhennogo programmirovanija [Search for solutions in production systems by methods of generalized programming] / Z.N. Rusakova // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal [International Research Journal]. No. 2 (104). 2021 Part 1. February. [in Russian]
- Rusakova Z.N. Dinamicheskie struktury dannyh i vychislitel'nye algoritmy Visual C++ [Dynamic data structures and computational algorithms of Visual C++ ] / Z.N. Rusakova. St. Petersburg, 2014, 272 p. [in Russian]
- Rusakova Z.N. Struktury dannyh v S++ [Data structures in C++] / Z.N. Rusakova, I.V. Rudakov. Moscow: Publishing House of Bauman Moscow State Technical University.2020, p. 157. [in Russian]
- Rusakova Z.N. Razrabotka instrumental'nyh sredstv dlja reshenija zadach prinjatija reshenij [Development of tools for solving decision-making problems] / Z.N. Rusakova // Intellektual'nye sistemy. Trudy Devjatogo mezhdunarodnogo simpoziuma [Intelligent systems. Proceedings of the Ninth International Symposium]. Moscow, RUSAKI, 2010, 773. [in Russian]