ПАРАМЕТРЫ ПРОЦЕССА РАСПРЕДЕЛЕНИЯ КОНСЕРВАНТОВ В РАСТИТЕЛЬНОМ СЫРЬЕ

ПАРАМЕТРЫ ПРОЦЕССА РАСПРЕДЕЛЕНИЯ КОНСЕРВАНТОВ В РАСТИТЕЛЬНОМ СЫРЬЕ

Научная статья

Юнин В.А.^{1, *}, Захаров А.М.², Зыков А.В.³

¹ORCID: 0000-0002-3435-7468;

² ORCID: 0000-0002-8111-1727;

³ ORCID: 0000-0003-3501-0543;

^{1, 2, 3} Институт агроинженерных и экологических проблем сельскохозяйственного производства - филиал ФГБНУ ФНАЦ ВИМ, Санкт-Петербург, Россия

* Корреспондирующий автор (vim_iaep[at]mail.ru)

Аннотация

Важнейшим направлением в технологии заготовки сена повышенной влажности в рулонах является консервирование его химическими препаратами в процессе прессования. Это позволяет заготавливать сено влажностью 25-30%, сократить время вымывания питательных веществ из растений при неблагоприятных погодных условиях и тем самым уменьшать потери при заготовке и хранении. Внесение жидких химических консервантов при заготовке кормов относиться к сложной научной и практической проблеме, так как процесс связан с одновременным взаимодействием нескольких факторов, в том числе растения, химического консерванта, различных технических средств, животного организма и человека. Поэтому необходимо учесть все основные особенности, чтобы получить от взаимодействия вышеуказанных факторов наибольший биологический, производственный и экологический эффект с наименьшими затратами труда и средств. В основе процесса распространения химических консервантов в растительном сырье лежит диффузия, т.е. перенос вещества из одной области в другую в пределах одной фазы при отсутствии перемешивания. Коэффициент кинематической диффузии, характеризующий процесс распространения консервантов в стебельчатой растительной массе, является постоянной величиной, определяющей эффективное распределение парообразной и жидкой фаз консерванта. Численное значение этого коэффициента находится в пределах между значениями коэффициента диффузии пара и жидкости. Так как численные значения коэффициентов диффузии консервантов в литературных источниках отсутствуют, необходимо провести экспериментальные исследования, с целью их определения.

Ключевые слова: консервант, диффузия, корм, хранение, параметр.

PARAMETERS OF THE DISTRIBUTION PROCESS OF PRESERVATIVES IN PLANT RAW MATERIALS

Research article

Yunin V.A.^{1, *}, Zakharov A.M.², Zykov A.V.³

¹ ORCID: 0000-0002-3435-7468;

² ORCID: 0000-0002-8111-1727;

³ ORCID: 0000-0003-3501-0543;

^{1, 2, 3} Institute of Agroengineering and Environmental Problems of Agricultural Production, branch of the All-Union Research Institute of Agricultural Mechanization, Saint Petersburg, Russia

^* Corresponding author (vim_iaep[at]mail.ru)

Abstract

The most important area in the technology of harvesting high-moisture hay in rolls is its preservation via chemical preparations during baling. This makes it possible to harvest hay with a humidity of 25-30%, reduce the time of leaching of nutrients from plants under adverse weather conditions and thereby reduce losses during harvesting and storage. The introduction of liquid chemical preservatives in the preparation of feed is a complex scientific and practical problem, since the process is associated with the simultaneous interaction of several factors, including plants, chemical preservatives, various technical means, as well as animals and humans. Therefore, it is necessary to take into account all the key aspects to get the greatest biological, industrial and environmental effect from the interaction of the aforementioned factors with the least labor and monetary costs. The process of distribution of chemical preservatives in plant raw materials is based on diffusion, the transfer of a substance from one region to another within one phase in the absence of mixing. The kinematic diffusion coefficient, which characterizes the process of spreading preservatives in the stalked plant mass, is a constant value that determines the effective distribution of the vaporous and liquid phases of the preservative. The numerical value of this coefficient is in the range between the values of the vapor and liquid diffusion coefficient. Since there are no numerical values of the diffusion coefficients of preservatives in the related literature, it is necessary to conduct experimental studies in order to determine them.

Keywords: preservative, diffusion, feed, storage, parameter.

Введение

Внесение жидких химических консервантов при заготовке кормов относиться к сложной научной и практической проблеме в связи с тем, что процесс связан с одновременным взаимодействием нескольких факторов, в том числе растения, химического консерванта, различных технических средств, животного организма и человека. Поэтому необходимо учесть все основные особенности, чтобы получить от взаимодействия вышеуказанных факторов наибольший биологический, производственный и экологический эффект с наименьшими затратами труда и средств.

Известно, что образование и накопление кормовой массы растений происходит в результате биохимических процессов, протекающих в клетках растений. Процессы, обеспечивающие накопление кормовой массы необходимо поддерживать, а процессы, разрушающие питательные вещества – по возможности затормаживать или полностью останавливать. Первые процессы протекают в растущих растениях, а вторые – в скошенной растительной массе, лишенной доступа к ней питательных веществ из почвы [1], [2].

Чтобы получить при заготовке высококачественный растительный корм, сведя к минимуму потери питательных и биологически активных веществ, необходимо сократить до минимума жизнедеятельность клеток скошенных растений.

Основным условием жизнедеятельности растений является обмен веществ, включающий два одновременно протекающих в противоположном направлении процесса – ассимиляции (усвоение) и диссимиляции (распад). Если в процессе ассимиляции растение строит свои клетки за счет веществ внешней среды, то при диссимиляции происходит расщепление углеводов с выделением энергии и образованием конечных продуктов.

Указанные биохимические процессы осуществляются с помощью белковых ферментов. Следовательно, все приемы, направленные на увеличение количества и активности ферментов, участвующих в процессах ассимиляции, будут способствовать синтезу кормовой массы, а все приемы, направленные на снижение количества и активности ферментов, участвующих в диссимиляционных превращениях веществ, будут способствовать распаду веществ и в конечном итоге – прекращению активности.

Процесс взаимодействия консерванта с микробной и растительной клеткой лучше всего протекает в жидкой среде, в связи с чем консерванты должны быть хорошо растворимы в водной среде и соках растений.

В основе процесса распространения химических консервантов в растительном сырье лежит диффузия, т.е. перенос вещества из одной области в другую в пределах одной фазы при отсутствии перемешивания. Опыты и теория показывают, что диффузия происходит при наличии градиента давления, градиента температуры, полей внешних сил и градиента концентрации.

Провяленное растительное сырье в поле, в котором происходит процесс диффузии, представляет собой субстрат, состоящий из стеблей и листьев, содержащих связанную влагу и воздух. Жидкий химический консервант, состоящий из собственной жидкости и пара, образующий на ее поверхности под воздействием градиентов концентрации и температуры, диффундирует в такой среде в основном в двух фазах: жидкой и парообразной (газообразной). Парообразная фаза химического консерванта диффундирует во внешнюю структуру растений со скоростью, пропорциональной градиенту концентрации диффундирующего вещества. Естественным препятствием на направлениях диффузии в растительном сырье являются стебли и листья растений, замедляющие ход процесса диффузии паров.

Методы и принципы исследования

При диффузии паров консервантов в растительном слое происходит сорбция влаги и паров растениями по закону, описываемому уравнением Брунауэра, Эммета, Теллера для растительных материалов влажностью до 35%[3], [4].

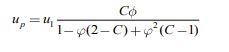(1)

где: u_p – равновесное влагосодержание материала при соответствующем режиме обработки, кг/кг;

 u₁- равновесное влагосодержание материала перед обработкой, кг/кг;

ф - относительная влажность паровоздушной смеси, безразмерная;

С- постоянная, характеризующая вид материала, безразмерная.

Решая уравнение 1 относительно величины  при условии максимального увлажнения растительного сырья парами консерванта, находим, что влагосодержание растений увеличивается незначительно, поэтому влиянием сорбции влаги из паров консерванта на процесс консервирования можно пренебречь.

Жидкая фаза консерванта, взаимодействуя с переносчиками белковой природы, диффундирует внутри растений, в которых растворителем является растительный сок, и участвует непосредственно в процессе подкисления корма.

Процессы диффузии пара и жидкости в растительном сырье классифицируются как однонаправленная диффузия и описываются общим уравнением:

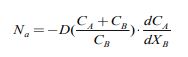(2)

где Na- число молей вещества А, диффундирующего в одном направлении через единицу поперечного сечения в единицу времени, моль;

D - кинематический коэффициент диффузии, м² /с;

C_A - концентрация диффундирующего вещества, кг/м³;

C_B- концентрация среды диффузии, кг/м³;

X_B- длина в направлении диффузии, м;

- градиент концентрации диффундирующего вещества по координате X.

Знак минус перед градиентом концентрации показывает, что концентрация  C_A уменьшается в направлении диффузии. Градиент концентрации  тем больше, чем больше сопротивление встречает диффузия молекул вещества А. Величина этого сопротивления пропорциональна концентрациям молекул в среде, в которой происходит диффузия. Она будет тем меньше, чем больше результирующая скорость молекул вещества растворителя в направлении, противоположном движению вещества.

Коэффициент кинематической диффузии D_AB представляет собой коэффициент пропорциональности между потоком компонента А и градиентом его в направлении диффузии и определяется в общем случае для газов по следующему рабочему уравнению Чэпмена и Энскога [5]:

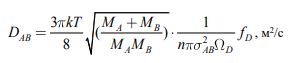(3)

где M_A, M_B - молекулярные массы растворенного вещества и растворителя, кг;

n - число молекул в 1 м³;

k - постоянная Больцмана;

T - температура, ^oC;

Ω- интеграл столкновений для диффузии (является функцией температуры и зависит от выбранного закона молекулярных сил взаимодействия сталкивающихся молекул);

Σ_АB - характеристическое расстояние (оно тоже зависит от выбранного закона межмолекулярных сил);

f_D - корректирующий член, имеющий значение порядка 1,0-1,1.

В случае диффузии паров химических консервантов через слой растительного сырья, происходящий при атмосферном давлении и при температуре в 23 ℃ влияние давления и температуры на коэффициент незначительно. Поэтому Ибрахим и Кулоор установили для диффузии газов и паров в воздух линейную зависимость от молекулярной массы M, и на этом основании предложили формулу [6]:

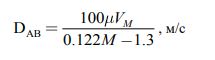(4)

где м - динамический коэффициент вязкости паров консервантов, Па·с;

 V_м- мольный объем паров, м³ /моль;

 М- молярная масса паров, кг/моль.

В слое растительного сырья с плотностью прессования в среднем 150 кг/м³ коэффициент кинематической диффузии меньше, по сравнению с диффузией пара в воздух.

Поэтому для расчета коэффициента диффузии в слое растительного сырья предлагают ввести поправочный коэффициент м_c = 1,7 [7].

Формула 3 с учетом этого коэффициента представляется в виде:

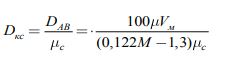(5)

где D_кс - расчетный коэффициент кинематической диффузии паров химических консервантов в среде растительных материалов, м²/с.

Результаты расчетов коэффициентов  для паров основных жидких консервантов представлены в таблице 1.1.

Паровая и жидкая фазы химических веществ находятся в равновесии, которое в общем случае описывается уравнением Клаузиуса – Клапейрона [8]:

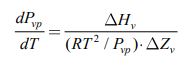(6)

где  P_vp- давление паров, Па;

- теплота парообразования, Дж/кг;

R- универсальная газовая постоянная;

T- температура, ⁰K;

Z_v- коэффициент сжимаемости пара.

Подставляя в уравнение 6 значения мольных объемов жидкости и пара, определяем теплоту парообразования:

(7)

где  V_Mn - мольный объем пара, м³ /моль;

V_Mж - мольный объем жидкости, м³ /моль;

 J- механический эквивалент теплоты.

Для расчета численных значений воспользуемся эмпирической интерпретацией уравнения 7:

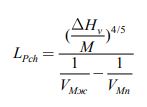(8)

где  - значение лиопарахора, вычисленное для химических консервантов по долям Боутена и Джонса [8]: - теплота парообразования, Дж/кг;

 M- молекулярная масса, кг/моль;

V_Mn , V_Mж- мольные объемы жидкой и паровой фаз, м³/моль.

Решая уравнения 8 относительно V_Mn, получим следующую зависимость:

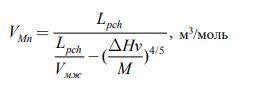(9)

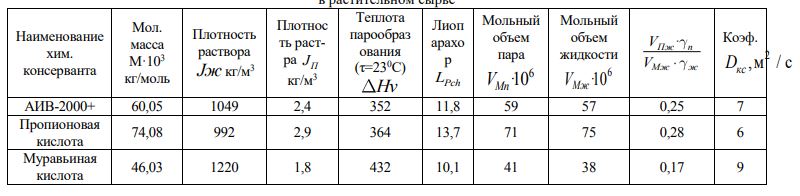
Исходные данные и результаты расчетов  D_кс приведены в таблице 1.

Основные результаты

Из-за отсутствия детально разработанной теории жидкого агрегатного состояния до сих пор еще невозможно точно представить механизм диффузии в жидкостях. Попытки разработать теоретически обоснованный метод расчета коэффициента кинематической диффузии в жидкостях не привели к удовлетворительным результатам [8]. В связи с тем, что физико-химические свойства растительного сока и воды мало отличаются друг от друга, представляется возможным использование полуэмпирических методов расчета коэффициента диффузии в бинарных смесях применительно к диффузии жидкой фазы химического препарата в соке растений.

Таблица 1 – Расчетные значения коэффициентов диффузии паров различных химических консервантов в растительном сырье

Согласно развитой Эйрингом теории абсолютной скорости процессов, молекулы диффундирующего вещества проникают в промежутки – «дыры» – между молекулами растворителя [7]. При этом коэффициент кинематической диффузии может быть определен как:

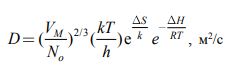(10)

где  V_m- мольный объем растворителя, м³ /моль;

T - абсолютная температура ^oK;

 - энтропия активации процесса диффузии;

- теплота активации процесса, Дж/кг;

N₀- число Авогадро;

k- постоянная Больцмана;

n- постоянная Планка;

R- газовая постоянная.

Основываясь на выводах статистической механики, Камаль и Канджар [4] вывели формулу, с помощью которой рассчитываются коэффициенты  со средней погрешностью 13%:

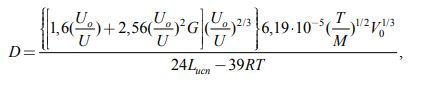(11)

где: ;

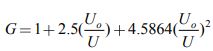 L_исп- теплота испарения растворенного вещества при температуре Т, ^oK;

 M- молекулярная масса, кг;

 R- газовая постоянная;

 U₀- объем одного моля, м³;

U - полный объем, приходящийся на одну молекулу, м³;

 V- объем, занимаемый одной молекулой, м³.

На основании полуэмпирических методов расчета кинематического коэффициента диффузии в жидкостях, рядом авторов [8] получены следующие основные зависимости коэффициента D.

Кинематический коэффициент диффузии D растворенного вещества 1 в растворителе 2 при температуре 20℃ по Арнольду [12] равен:

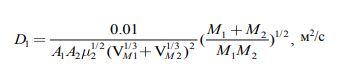(12)

где  A_1,A₂ - поправочные коэффициенты, характеризующие вещество 1 и 2;

м₂ - динамический коэффициент вязкости растворителя, Па·с;

 V_M1, V_M2- мольные объемы растворенного вещества 1 и растворителя 2, рассчитанные суммированием долей по Леба [6], моль/м³;

M₁, M₂ - молекулярные массы вещества 1 и 2, кг.

Уилк и Ченг [6] предложили следующую зависимость:

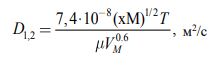(13)

где M - молекулярная масса диффундирующего вещества, кг/моль;

м - динамический коэффициент вязкости, Па·с;

х - коэффициент характеризующий процесс ассоциации в растворителе (для воды  =2,6).

Для близких значений мольных объемов диффундирующего вещества и растворителя Шейбель предложил следующее уравнение [7]:

Погрешность расчетов в случае применения воды в качестве растворителя составляет ± 9% [3].

Для водных растворов Стимер и Текер [7] предложили формулу в диапазоне температур t ˃ 20,5 ℃

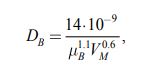(16)

где D_B- коэффициент диффузии в разбавленном водном растворе при t= 20℃, м²/с;

M_B - динамический коэффициент вязкости воды при температуре 20℃, мПа·с.

Результаты расчета коэффициентов кинематической диффузии для химических консервантов в жидкой среде представлены в таблице 2.

Таблица 2 – Результаты расчета коэффициентов кинематической диффузии для химических консервантов в жидкой среде

Наименование хим. консерванта	Растворимость в воде	Плотность раствора кг/м3 при концентрации %			Молекулярная масса раствора М 103, кг/моль при концентрации %			Мольный объем раствора Vж 106, м3/моль при концентрации %			Коэффициент диффузии D 109, м2·с при концентрации %
		90	60	30	90	60	30	90	60	30	90	60	30
АИВ-2000+	+	1049	1030	1015	60	44	31	57	42	30	1,2	1,5	1,8
Пропионовая кислота	+	992	994	998	74	52	35	75	52	35	1,1	1,3	1,1
Муравьиная кислота	+	1220	1132	1066	46	35	26	38	31	25	1,6	1,8	2,0

Заключение

Из приведенного выше, следует, что жидкие химические консерванты, являющиеся, как правило, органическими летучими соединениями семейства карбоновых кислот, обладают значительной фугитивностью процесса парообразования. Поэтому, после введения определенной массы жидкости в растительное сырье одновременно происходит два процесса диффузии: диффузия паров кислот в воздушные промежутки растительного сырья и диффузия жидкой фазы консерванта внутри стеблей растений.

Установлено, что соотношение между парообразной и жидкой фазами химических консервантов можно характеризовать следующими данными: муравьиная кислота – 0,16%; AIV2000 Плюс – 0,28; пропионовая кислота – 0,25.

Коэффициент кинематической диффузии , характеризующий процесс распространения консервантов в стебельчатой растительной массе, является постоянной величиной, определяющей комплексное (эффективное) распределение парообразной и жидкой фаз консерванта. Численное значение этого коэффициента находится в пределах между значениями коэффициента диффузии пара и жидкости. Так как численные значения коэффициентов диффузии консервантов в литературных источниках отсутствуют, необходимо провести экспериментальные исследования, с целью их определения. В дальнейшем использование коэффициента диффузии при математическом моделировании процесса воздействия консерванта на растительном сырье позволит определить характер изменения концентрации консерванта в растительном материале и на его основе установить параметры работы оборудования.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. CoblentzW.K. Effects of a propionic acid-based preservative on storage characteristics, nutritive value, and energy content for alfalfa hays packaged in large round bales1 /W.K. Coblentz, M.G. Bertram // Journal of Dairy Science, Volume 95, 2012; Issue 1, Pages 340-352.
2. Coblentz, W.K. Nutritive value and fermentation characteristics of alfalfa-mixed grass forage wrapped with minimal stretch film layers and stored for different lengths of time /W.K. Coblentz, R.K.Ogden, M.S. Akins et al. // Journal of Dairy Science. 100. DOI: 10.3168/jds.2016-12404.
3. Baah J. Effect of Lactobacillus buchneri 40788 and Buffered Propionic Acid on Preservation and Nutritive Value of Alfalfa and Timothy High-moisture Hay Asian-Australas /J. Baah, T. McAllister, L. Bos et al.// J Anim Sci 2005;18(5):649-660. DOI: 10.5713/ajas.2005.649
4. Поташников П.Ф. Использование метода Брунауэра-Эммета-Теллерадляанализавнутреннейструктурыупаковочных картонов / П.Ф. Поташников, Л.Ю. Комарова// Вестник МГУП имени Ивана Федорова. – 2012. – №12. – С. 114 – 119.
5. Галкин, В.С. Преобразование уравнений первого приближения методом Чепмена -Энскога и векторные соотношения переноса для смесей многокомпонентных газов / В.С. Галкин// ПММ. -2007. -Т. 71. -Вып. 2. -С. 301 -302.
6. Новоселов А.Г. Молекулярная диффузия газов в жидкости. Коэффициенты молекулярной диффузии диоксида углерода в воде / А.Г. Новоселов // Научный журнал НИУ ИТМО. Серия: Процессы и аппараты пищевых производств. – 2014. – №2. – С. – 19.
7. Шишацкий Ю.И. Определение коэффициентов диффузии экстрактивных веществ в люпине / Ю.И.Шишацкий, С.Ю.Плюха, С.С. Иванов // Вестник ВГУИТ. – 2014. – №2. – С. 28 – 32.
8. Валге A.M. Оценка эффективности технологических процессов заготовки кормов из трав / A.M.Валге, А.И. Сухопаров // Технологии и технические средства механизированного производства продукции растениеводства и животноводства. 2018. № 3 (96). С. 129-138. DOI: 10.24411/0131-5226-2018-10066

Список литературы на английском языке / References in English

1. CoblentzW.K. Effects of a propionic acid-based preservative on storage characteristics, nutritive value, and energy content for alfalfa hays packaged in large round bales1 /W.K. Coblentz, M.G. Bertram // Journal of Dairy Science, Volume 95, 2012; Issue 1, Pages 340-352.
2. Coblentz, W.K. Nutritive value and fermentation characteristics of alfalfa-mixed grass forage wrapped with minimal stretch film layers and stored for different lengths of time /W.K. Coblentz, R.K.Ogden, M.S. Akins et al. // Journal of Dairy Science. 100. DOI: 10.3168/jds.2016-12404.
3. Baah J. Effect of Lactobacillus buchneri 40788 and Buffered Propionic Acid on Preservation and Nutritive Value of Alfalfa and Timothy High-moisture Hay Asian-Australas /J. Baah, T. McAllister, L. Bos et al.// J Anim Sci 2005;18(5):649-660. DOI: 10.5713/ajas.2005.649
4. Potashnikov P.F. Ispol`zovanie metoda Brunaue`ra-E`mmeta-Tellera dlya analiza vnutrennej struktury` upakovochny`x kartonov [The use of the Brunauer-Emmett-Teller method for analyzing the internal structure of packaging cartons] / P.F.Potashnikov, L.Yu. Komarova // Vestnik MGUP imeni Ivana Fedorova. – 2012. – №12. – P. 114 – 119. [in Russian]
5. Galkin, V.S. Preobrazovanie uravnenij pervogo priblizheniya metodom Chepmena -E`nskoga i vektorny`e sootnosheniya perenosa dlya smesej mnogokomponentny`x gazov [Transformation of the first approximation equations by the Chapman-Enskog method and vector transfer relations for mixtures of multicomponent gases] /V.S. Galkin// PMM. -2007. -Vol. 71. -Issue. 2. - P. 301 -302. [in Russian]
6. Novoselov A.G. Molekulyarnaya diffuziya gazov v zhidkosti. Koe`fficienty` molekulyarnoj diffuzii dioksida ugleroda v vode [Molecular diffusion of gases in a liquid. Coefficients of molecular diffusion of carbon dioxide in water] /A.G. Novoselov // Nauchny`j zhurnal NIU ITMO. Seriya: Processy` i apparaty` pishhevy`x proizvodstv. – 2014. – №2. – P. 19. [in Russian]
7. Shishaczkij Yu.I. Opredelenie koe`fficientov diffuzii e`kstraktivny`x veshhestv v lyupine [Determination of diffusion coefficients of extractive substances in lupine] /Yu.I.Shishaczkij, S.Yu.Plyuxa, S.S. Ivanov // Vestnik VGUIT. – 2014. – №2. – P. 28 – 32. [in Russian]
8. Valge A.M. Ocenka e`ffektivnosti texnologicheskix processov zagotovki kormov iz trav [Evaluation of the efficiency of technological processes of forage harvesting from herbs] /A.M.Valge, A.I. Suxoparov // Texnologii i texnicheskie sredstva mexanizirovannogo proizvodstva produkcii rastenievodstva i zhivotnovodstva. 2018. № 3 (96). P. 129-138. DOI:10.24411/0131-5226-2018-10066[in Russian]