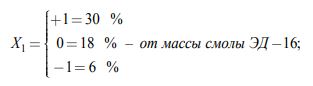ОПТИМИЗАЦИЯ ПОЛИМЕРНОЙ МАТРИЦЫ ЭПОКСИДНЫХ КОМПОЗИТОВ

ОПТИМИЗАЦИЯ ПОЛИМЕРНОЙ МАТРИЦЫ ЭПОКСИДНЫХ КОМПОЗИТОВ

Научная статья

Бормотов А.Н.^*

ORCID: 0000-0001-7069-6603,

Пензенский государственный технологический университет, Пенза, Россия

^* Корреспондирующий автор (aleks21618[at]yandex.ru)

Аннотация

В работе исследуются процессы отверждения ненаполненных эпоксидных смол ЭД-16. Выполнено математическое моделирование процессов отверждения и приводятся математические модели процессов отверждения в виде полных квадратичных полиноминальных моделей. Отдельно исследуется степень отверждения ненаполненных эпоксидных композиций. В результате исследования полученных моделей и выполнения процедур оптимизации для смолы ЭД-16 разработаны теоретические аспекты отверждения высоковязких эпоксидных систем и предложены рецептурно-технологические параметры получения высокопрочной полимерной матрицы на основе высоковязкой смолы ЭД-16, позволяющей получать эпоксидные композиты с заданными параметрами структуры и свойств.

Ключевые слова: композиционные материалы, математическое моделирование, оптимальная структура, оптимизация свойств.

OPTIMIZATION OF THE POLYMER MATRIX OF EPOXY COMPOSITES

Research article

Bormotov A.N.^*

ORCID: 0000-0001-7069-6603,

Penza State Technological University, Penza, Russia

^* Corresponding author (aleks21618[at]yandex.ru)

Abstract

The paper investigates the curing processes of the unfilled epoxy resins ED-16. The author performs a mathematical simulation of curing processes and presents mathematical models of curing processes in the form of complete quadratic polynomial models. The article also features a separate study of the degree of curing of unfilled epoxy compositions. As a result of studying the obtained models and performing optimization procedures for ED-16 resin, the article develops theoretical aspects of curing high-viscosity epoxy systems as well as  proposes formulation and technological parameters for obtaining a high-strength polymer matrix based on the high-viscosity ED-16 resin, which allows for obtaining epoxy composites with specified structure and properties parameters.

Keywords: composite materials, mathematical modeling, optimal structure, optimization of properties.

Введение

В настоящее время современное строительство для изготовления строительных конструкций, отделочных элементов зданий и сооружений остро нуждается в композиционных строительных материалах, которые отличаются высокими эксплуатационными характеристиками и имеют строго заданную структуру и свойства. Например, композиционные строительные материалы для защиты от радиации должны обладать некоторыми специфическими свойствами: высокой средней плотностью, наличием элементов с большими атомными номерами, отсутствием кристаллической решётки, минимальным содержанием элементов, образующих долгоживущие нуклиды, и т.д. [1], [2].

Наибольший практический интерес представляет возможность получения композиционных строительных материалов с высокими физико-механическими и эксплуатационными свойствами при минимальных затратах времени и материальных ресурсов. Решение этой задачи не возможно без оптимальной во всех смыслах полимерной матрицы. Такая полимерная матрица должна иметь оптимальные реологические характеристики [3], [4] и высокие физико-механические показатели. В качестве факторов, оказывающих наиболее сильное влияние на физико-механические показатели, являют концентрация отвердителя и прогрев полимерной матрицы [5], которые при оптимальном соотношении обеспечивают максимальную степень отверждения эпоксидной смолы.

Методы и принципы исследования

При создании эпоксидных композитов для защиты от радиации в качестве связующего использовали эпоксидно-диановую смолу марки ЭД-16, отверждаемую полиэтиленполиамином (ПЭПА). Выбор смолы обусловлен более высокой молекулярной массой по сравнению с другими марками, что должно обеспечивать лучшую защиту от действия высокоэнергетических излучений.

Для оценки степени отверждения эпоксидной смолы использовался метод дифференциальной сканирующей калориметрии (ДСК) [6], основанный на измерении тепла, выделяющегося при реакции отверждения эпоксидных смол, с использованием прибора DSC6000 фирмы PerkinElmer.

Степень отверждения– величина (%), характеризующая степень протекания реакции отверждения эпоксидной смолы. Степень отверждения вычисляют по формуле (1).

(1)

где: – H_S – общая теплота реакции испытуемой (частично) отвержденной эпоксидной композиции, Дж/г; H_T – общая теплота реакции отверждения, определенная в предварительном испытании, Дж/г [6].

Общая теплота реакции– общее количество тепла (Дж/г), выделяемое неотвержденной эпоксидной композицией в процессе полного протекания реакции отверждения, определенную методом ДСК [6].

Для большинства реальных материаловедческих, рецептурно-технологических и технико-экономических задач целесообразно применять полиноминальные модели [7], поэтому в данной работе для описания поведения системы использовали полиноминальные экспериментально-статистические модели (ЭС-модели) вида:

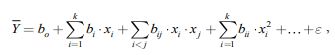(2)

где b_o, b_i, b_ij, b_ii – определяются как статистические величины в нормализованном виде по экспериментальным данным;e – случайная величина, учитывающая совокупность ошибок эксперимента.

Причём, учитывая точность приборов и инструментов, используемых при проведении экспериментов, достаточно уравнения регрессии второго порядка. При использовании уравнений более высоких степеней точность оценок коэффициентов уравнений регрессии будет превышать точность определения экспериментальных данных, и уравнение регрессии будет неадекватно при проверке по критерию Фишера. Исходя из этого, в данной работе применялись полные квадратичные ЭС-модели. Такие модели позволяют производить полный регрессионный анализ, результатом которого является решение оптимизационной задачи первого вида – отыскание оптимальных условий функционирования системы при любом расходе ресурса и второго вида – отыскание минимального расхода ресурса для обеспечения требуемого уровня показателя качества системы [7].

Для оптимизации полимерной матрицы был выбран девятиточечный композиционный симметричный план ПФЭ 3², имеющий высокую эффективность по критериям D, A, E и Q, который легко анализируется и позволяет представить результаты графически. Его целесообразно применять всегда, когда неизвестно направление поиска и нет жёстких ограничений на ресурсы.

Факторы и интервалы их варьирования были выбраны следующие:

фактор X₁ – концентрация отвердителя ПЭПА, интервалы варьирования:

фактор X₂ – температура прогрева образцов, интервалы варьирования:

Основные результаты

Формирование структуры эпоксидных композитов повышенной плотности осуществляли с использованием основных положений полиструктурной теории, теории оптимального управления и методов системного анализа. Сущность полиструктурной теории состоит в представлении материала полиструктурным, то есть в выделении в единой структуре многих взаимозависимых структур, прорастающих одна в другую (по принципу «структура в структуре»). Выделение систем и подсистем, иерархия критериев качества, оптимизация режимов формирования отдельных структур в полиструктуры – все это и определяет рецептуру и технологию изготовления композитов [8].

Расчёты коэффициентов уравнений регрессий, их оценок, доверительных интервалов, проверки критериев Стьюдента и Фишера и т.д. проводили в соответствии с методикой, изложенной в [7] при помощи программы Mathcad v.14. После проведения всех статистических расчётов было получено окончательное уравнение регрессии:

(3)

В натуральном виде уравнение (3) имеет вид:

(4)

где R_сж (С, Т) – предел прочности при сжатии ненаполненных образцов размером 20´20´20 мм; С – концентрация ПЭПА в % – оптимизируемый фактор X₁; Т – температура прогрева в ^оС – оптимизируемый фактор X₂.

После исследования и решения данного уравнения регрессии на экстремум были получены следующие значения R_сж (С, Т), С и Т:

• R_max = 129,79» 130 MPa – предел прочности при сжатии;
• С = – 0,252» 15 % – концентрация отвердителя от массы смолы;
• Т = 1» 80 ^оС – температура прогрева изделий.

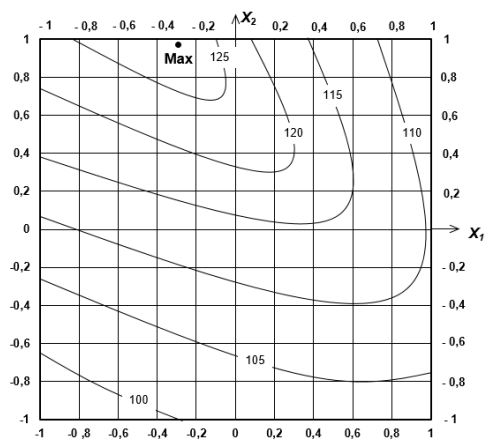
По этим данным была построены изолинии результирующей функции (области равных оценок), на которой отображены результаты оптимизации (рис. 1). Как видно из рисунка 1, уравнение (4) имеет чётко выраженный максимум, соответствующий 15 %-ной (от массы смолы) концентрации отвердителя и температуре прогрева изделий 80 ^оС в течение 5 часов.

Для проверки результатов математического моделирования и оптимизации рецептурно-технологических параметров полимерной матрицы эпоксидных композитов была определена степень отверждения ненаполненной смолы в условиях уровнях варьирования второго фактора методом ДСК [6].

Рис. 1 – Изолинии прочности полимерной матрицы

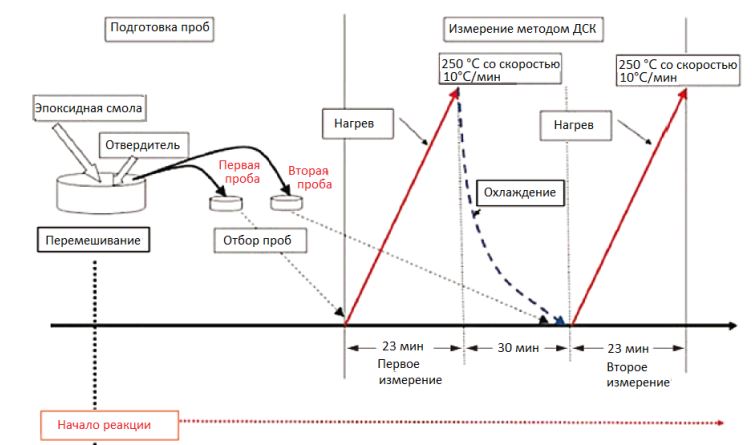
Процедура выполнения измерения степени отверждения изображена на рисунке 2.

Рис. 2 – Процедура выполнения измерения степени отверждения

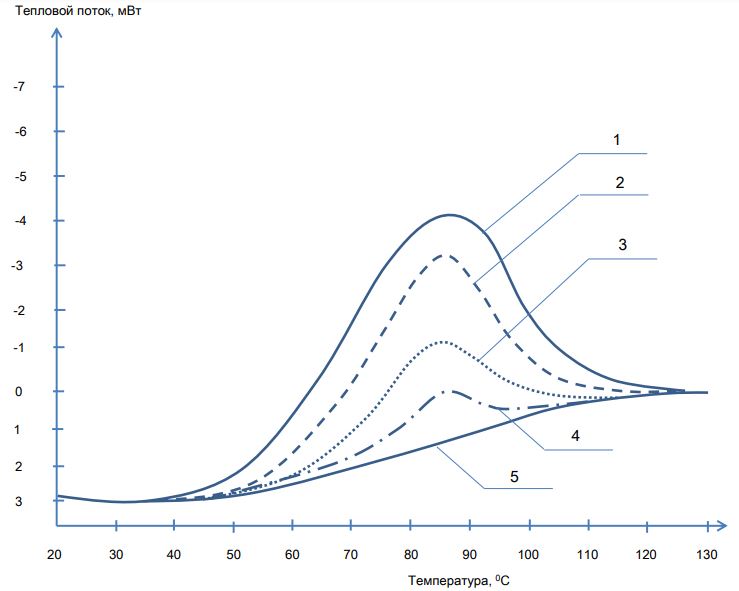
За начало экзотермической реакции принимали момент отклонения на кривой ДСК теплового потока от базовой линии (левый предел интегрирования ДСК кривой), за окончание экзотермической реакции принимали момент выхода на кривой ДСК правой ветви теплового потока на базовую линию (правый предел интегрирования ДСК кривой), рисунок 3. Ввиду значительной разнице высот базовых линий до и после процесса отверждения выполняли интегрирование с помощью сигмоидальной базовой линии, рисунок 3.

Рис. 3 – Определение площади между кривыми ДСК и сигмоидальной базовой линией:

1 – неотвержденная эпоксидная композиция;2 – прогрев при температуре 40 ⁰С в течение 5 часов; 3 – прогрев при температуре 60 ⁰С в течение 5 часов;4 – прогрев при температуре 80 ⁰С в течение 5 часов;  5 – базовая линия, соответствующая полному отверждению эпоксидной композиции

Степень отверждения частично отвержденной эпоксидной композиции определяли по отношению теплоты реакции этой композиции к общей теплоте реакции неотвержденной эпоксидной композиции по формуле (1).

После обработки эксперимента согласно методике, изложенной в [6], были получены результаты:

• степень отверждения 72,4% при прогреве при температуре 40 ⁰С в течение 5 часов;
• степень отверждения 85,1% при прогреве при температуре 60 ⁰С в течение 5 часов;
• степень отверждения 98,5% при прогреве при температуре 80 ⁰С в течение 5 часов.

Заключение

По частным производным от обоих переменных в уравнении (3) видно, что зависимость прочности от температуры прогрева имеет прямо пропорциональный характер, а от концентрации отвердителя – параболический. Это можно объяснить тем, что, увеличивая температуру прогрева, мы уменьшаем размеры глобул трехмерной сетки и увеличиваем степень полимеризации смолы, что приводит к упорядочиванию структуры и улучшению физико-механических свойств. Образующиеся в процессе твердения зародыши полимерной фазы дисперсно распределены по объёму и фактически играют роль наполнителей. Таким образом, твердеющие ненаполненные полимерные системы на определённом этапе формирования структуры можно считать наполненными естественным образом. Учитывая, что на определённом этапе твердения двухфазные полимерные системы за счёт кластерообразования стремятся достичь состояния термодинамического равновесия, то параболическая зависимость показывает существование такого количества отвердителя,прикотором появлениезародышейполимернойфазы,ихсамоорганизация–кластерообразование, а, следовательно, достижение термодинамического равновесия происходит за самое короткое время и в самом полном объёме.

Эксперименты по определению степени отверждения подтверждают выбранные при математическом моделировании технологические параметры температурного прогрева эпоксидных композиций.

Изложенная в статье методология оптимизации полимерной матрицы на основе эпоксидных композиций была многократно апробирована различными учеными при синтезе композиционных материалов с заданными параметрами структуры и свойств [1], [3], [9], [15].

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Бормотов А.Н. Математическое моделирование и многокритериальных синтез композиционных материалов специального нахначения/А.Н.Бормотов: дис. … доктора. техн. наук – Пенза, Пензенский государственный технологический университет, 2011. – 275 с.
2. Giustozzi, F. Shear rheology and microstructure of mining material-bitumen composites as filler replacement in asphalt mastics / Filippo Giustozzi, Kyrollo Smansour, Federico Patti et al. // Construction and Building Materials, Volume 171,2018, pp. 726-735. DOI: 10.1016/j.conbuildmat.2018.03.190.
3. Бормотов, А.Н. Моделирование влияния модифицирующих добавок на реологические показатели композитов / Бормотов А.Н., Горохова А.А. // Международный научно-исследовательский журнал. – №4 (106). – Часть 1. – 2021. – С. 51-56. DOI: 10.23670/IRJ.2021.106.4.008.
4. Бормотов, А.Н. Математическаямодельвязкостиненаполненнойэпоксиднойсмолы / А.Н. Бормотов, А.А. Горохова // Международныйнаучно-исследовательскийжурнал. – №4 (94). – Часть 1. – 2020. – С. 23-31. DOI: 23670/IRJ.2020.94.4.003.
5. Mphahlele, К. Cure kinetics, morphology development, and rheology of a high-performance carbon-fiber-reinforced epoxy composite / Keletso Mphahlele, Suprakas Sinha Ray, Andrei Kolesnikov // Part B: Engineering. – Volume 176, 2019, 107300. DOI: 10.1016/j.compositesb.2019.107300
6. ГОСТ Р 57687-2017. «Пластмассы. Эпоксидные смолы. Определение степени отверждения эпоксидных смол с применением дифференциальной сканирующей калориметрии» от 01.02.2018. – М.: АНО "Стандарткомпозит", 2018. – 10 с.
7. Вознесенский В.А. Численные методы решения строительно-технологических задач на ЭВМ / В.А. Вознесенский и др..Киев, 1989. – 119 с.
8. Соломатов В.И. Элементы общей теории композиционных строительных материалов / В.И. Соломатов // Материалы юбилейной конференции: Успехи строительного материаловедения. – М.: МИИТ, 2001. – С. 41-56.
9. Гайфутдинов А.М. Мониторинг процесса отверждения эпоксидных связующих для композиционных материалов / А.М. Гайфутдинов // XXIV Туполевские чтения (школа молодых ученых).Тексты докладов участников Международной молодёжной научной конференции, в 6 т., 2019. – С. 399-402.
10. Хасимова, А.С. Литой бетон на основе композиционного гипсового вяжущего / А.С. Хасимова, Н.Н. Морозова, В.Г. Хозин // Технологии бетонов. – 2015.– №3-4 (104-105). – С. 23-25.
11. Завражин, Д. О. Основы реологии полимеров и технологические методы переработки полимерных материалов : учебное пособие / Д.О. Завражин, О.Г. Маликов, П.С. Беляев. — Тамбов : Тамбовский государственный технический университет, ЭБС АСВ, 2017. – 109 c.
12. Keon-SooJang. Mechanics and rheology of basalt fiber-reinforced polycarbonate composites / Keon-SooJang // Polymer. –Volume 147,2018, Pp. 133-141. DOI: 1016/j.polymer.2018.06.004
13. Fuchs, L. Numerical modeling of the effect of composite rheology on internal deformation in down-built diapirs / Lukas Fuchs, Hemin Koyi,Harro Schmeling / Tectonophysics. – Volume 646, 2015, Pp. 79-95. DOI: 1016/j.tecto.2015.01.014
14. Tang,Z. Optimization of rheological parameters and mechanical properties of Engineered Cementitious Composites (ECC) using regression-based models / Zixuan Tang, Chrysoula Litina, Abir Al-Tabbaa / Construction and Building Materials. – Volume 310, 2021, 125281. DOI: 1016/j.conbuildmat.2021.125281
15. Белов В.В. Капиллярная аутогезия в трехфазных сырьевых смесях / В.В. Белов // Фундаментальные, поисковые и прикладные исследования Российской академии архитектуры и строительных наук по научному обеспечению развития архитектуры, градостроительства и строительной отрасли Российской Федерации в 2018 году.– Российская академия архитектуры и строительных наук. – Москва, 2019. – С. 58-68.

Список литературы на английском языке / References in English

1. Bormotov A.N. Matematicheskoe modelirovanie i mnogokriterial'nyh sintez kompozicionnyh materialov special'nogo nahnacheniya [Mathematical modeling and multicriteria synthesis of composite materials of special purpose] /A.N.Bormotov: dis. … doktora. tekhn. nauk – Penza, Penza State Technological University, 2011. – 275 p. [in Russian]
2. Giustozzi, F. Shear rheology and microstructure of mining material-bitumen composites as filler replacement in asphalt mastics / Filippo Giustozzi, Kyrollo Smansour, Federico Patti et al. // Construction and Building Materials, Volume 171,2018, pp. 726-735. DOI: 10.1016/j.conbuildmat.2018.03.190.
3. Bormotov, A.N.Modelirovanie vliyaniya modificiruyushchih dobavok na reologicheskie pokazateli kompozitov [Modeling of the effect of modifying additives on rheological parameters of composites] / A.N.Bormotov, A.A. Gorohova // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal [International Scientific Research Journal]. – №4 (106). – Vol. 1. – 2021. – Pp. 51-56. DOI: 10.23670/IRJ.2021.106.4.008 [in Russian]
4. Bormotov, A.N. Matematicheskaya model' vyazkosti nenapolnennoj epoksidnoj smoly [Mathematical model of the viscosity of unfilled epoxy resin] / A.N. Bormotov, A.A. Gorohova // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal [International Scientific Research Journal]. – №4 (94). – Vol. 1. – 2020. – Pp. 23-31. DOI: 10.23670/IRJ.2020.94.4.003 [in Russian]
5. Mphahlele, К. Cure kinetics, morphology development, and rheology of a high-performance carbon-fiber-reinforced epoxy composite / Keletso Mphahlele, Suprakas Sinha Ray, Andrei Kolesnikov // Part B: Engineering. – Volume 176, 2019, 107300. DOI: 10.1016/j.compositesb.2019.107300
6. GOST R 57687-2017. «Plastmassy. Epoksidnye smoly. Opredelenie stepeni otverzhdeniya epoksidnyh smol s primeneniem differencial'noj skaniruyushchej kalorimetrii» [Plastics. Epoxy resins. Determination of the degree of curing of epoxy resins using differential scanning calorimetry] ot 01.02.2018. – M.: ANO "Standartkompozit", 2018. – 10 p. [in Russian]
7. Voznesenskij V.A. CHislennye metody resheniya stroitel'no-tekhnologicheskih zadach na EVM [Numerical methods for solving construction and technological problems on a computer] /V.A.Voznesenskij et al. Kiev, 1989. – 119 p. [in Russian]
8. Solomatov V.I. Elementy obshchej teorii kompozicionnyh stroitel'nyh materialov [Elements of the general theory of composite building materials] /V.I. Solomatov // Materialy yubilejnoj konferencii: Uspekhi stroitel'nogo materialovedeniya [Proceedings of the anniversary conference: Advances in building materials]. – M.: MIIT, 2001. – Pp. 41-56. [in Russian]
9. Gajfutdinov A.M. Monitoring processa otverzhdeniya epoksidnyh svyazuyushchih dlya kompozicionnyh materialov [Monitoring of the curing process of epoxy binders for composite materials] / A.M. Gajfutdinov // XXIV Tupolevskie chteniya (shkola molodyh uchenyh). Teksty dokladov uchastnikov Mezhdunarodnoj molodyozhnoj nauchnoj konferencii, v 6 t. [In the collection: XXIV Tupolev readings (school of young scientists). Texts of reports of participants of the International Youth Scientific Conference, in 6 volumes], 2019. – Pp. 399-402. [in Russian]
10. Hasimova, A.S. Litoj beton na osnove kompozicionnogo gipsovogo vyazhushchego [Cast concrete based on composite gypsum binder] / A.S. Hasimova, N.N. Morozova, V.G. Hozin // Tekhnologii betonov [Technologies of concrete]. – 2015. – № 3-4 (104-105). – Pp. 23-25. [in Russian]
11. Zavrazhin, D. O. Osnovy reologii polimerov i tekhnologicheskie metody pererabotki polimernyh materialov : uchebnoe posobie [Fundamentals of polymer rheology and technological methods of polymer materials processing : textbook] / O. Zavrazhin, O.G. Malikov, P.S. Belyaev. — Tambov : Tambovskij gosudarstvennyj tekhnicheskij universitet [Tambov : Tambov State Technical University], ELE ASV, 2017. – 109 p. [in Russian]
12. Keon-SooJang. Mechanics and rheology of basalt fiber-reinforced polycarbonate composites / Keon-SooJang // Polymer. –Volume 147,2018, Pp. 133-141. DOI: 1016/j.polymer.2018.06.004
13. Fuchs, L. Numerical modeling of the effect of composite rheology on internal deformation in down-built diapirs / Lukas Fuchs, Hemin Koyi,Harro Schmeling / Tectonophysics. – Volume 646, 2015, Pp. 79-95. DOI: 1016/j.tecto.2015.01.014
14. Tang,Z. Optimization of rheological parameters and mechanical properties of Engineered Cementitious Composites (ECC) using regression-based models / Zixuan Tang, Chrysoula Litina, Abir Al-Tabbaa / Construction and Building Materials. – Volume 310, 2021, 125281. DOI: 1016/j.conbuildmat.2021.125281
15. Belov V.V. Kapillyarnaya autogeziya v trekhfaznyh syr'evyh smesyah [Capillary autohesia in three-phase raw materials mixtures] / V.V. Belov // Fundamental'nye, poiskovye i prikladnye issledovaniya Rossijskoj akademii arhitektury i stroitel'nyh nauk po nauchnomu obespecheniyu razvitiya arhitektury, gradostroitel'stva i stroitel'noj otrasli Rossijskoj Federacii v 2018 godu [In the collection: Fundamental, exploratory and applied research of the Russian Academy of Architecture and Construction Sciences on scientific support for the development of architecture, urban planning and the construction industry of the Russian Federation in 2018]. – Rossijskaya akademiya arhitektury i stroitel'nyh nauk [Russian Academy of Architecture and Construction Sciences]. – Moskva, 2019. – Pp. 58-68.[in Russian]