РЕКУРРЕНТНОЕ ПРЕДСТАВЛЕНИЕ БАЗИСА ПЕРЕХОДА ОТ КОЭФФИЦИЕНТОВ РАЗЛОЖЕНИЯ ПО ФУНКЦИЯМ ЧЕБЫШЕВА-ЭРМИТА К ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЮ

РЕКУРРЕНТНОЕ ПРЕДСТАВЛЕНИЕ БАЗИСА ПЕРЕХОДА ОТ КОЭФФИЦИЕНТОВ РАЗЛОЖЕНИЯ ПО ФУНКЦИЯМ ЧЕБЫШЕВА-ЭРМИТА К ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЮ

Научная статья

Бочкарев А.В.^1, *, Сайфуллин Р.Т.²

¹ ORCID: 0000-0003-1615-5659;

² ORCID: 0000-0001-7047-3979;

^{1, 2} Самарский Государственный Технический Университет, Самара, Россия

* Корреспондирующий автор (bochkarevpubliciit[at]gmail.com)

Аннотация

Цель работы заключается в формировании рекуррентного представления для базиса, позволяющего по коэффициентам разложения исходного сигнала в базисе функций Чебышева-Эрмита восстановить массив вейвлет-коэффициентов исходного сигнала. В качестве вейвлетов в работе используются производные функции Гаусса m-го порядка. Рекуррентное представление необходимо для сокращения времени вычислений. Рекуррентное представление рассматриваемого базиса формируется на основе свойств полиномов Эрмита, входящих в состав производных функции Гаусса и функций Чебышева-Эрмита. Благодаря использованию полученных формул расчета вейвлет-коэффициентов с учетом описанного алгоритма их применения удается построить быстрые вычислительные алгоритмы обработки сигналов.

Ключевые слова: функции Чебышева-Эрмита, вейвлет-преобразование, вейвлеты Гаусса, разложение сигнала.

RECURRENT REPRESENTATION OF THE TRANSITION BASIS FROM THE EXPANSION COEFFICIENTS BASED ON THE CHEBYSHEV-HERMITE TO THE WAVELET TRANSFORM

Research article

Bochkarev A.V.^1, *, Saifullin R.T.²

¹ ORCID: 0000-0003-1615-5659;

² ORCID: 0000-0001-7047-3979;

^{1, 2} Samara State Technical University, Samara, Russia

* Corresponding author (bochkarevpubliciit[at]gmail.com)

Abstract

The aim of the work is to form a recurrent representation for the basis that allows for reconstructing an array of wavelet coefficients of the original signal from the expansion coefficients of the source signal in the basis of Chebyshev-Hermite functions. The derivatives of the Gauss function of the m order are used as wavelets.  The recurrent representation is necessary to reduce the calculation time. The recurrent representation of the studied basis is formed according to the properties of Hermite polynomials that are part of the derivatives of the Gauss function and the Chebyshev-Hermite functions. Because of the use of the obtained formulas for calculating the wavelet coefficients, taking into account the described algorithm for their application, it is possible to build fast computational algorithms for signal processing.

Keywords: Chebyshev-Hermite functions, wavelet transform, Gaussian wavelets, signal decomposition.

Введение

Одним из подходов к созданию алгоритмов обработки сигналов является кодирование сигнала в базисе функций Чебышева-Эрмита с последующим декодированием по другим, предварительно рассчитанным базисам; причем, в зависимости от выбора базиса возможно получить сам сигнал [1], [2], производную различных порядков [2], вейвлет преобразование [3], [4] и т.п.

Функции Чебышева-Эрмита находят широкое распространение в различных областях науки и техники. Так, их повсеместно применяют в математике, к примеру, в работе [5] изучается вопрос нахождения приближенных решений нелинейных дифференциальных уравнений с использованием спектрального метода, в работах [6] и [7] исследуется тот же вопрос с применением проекционного метода. В работе [8] описано применение данных функций для построения ортогонального банка фильтров, поскольку функции обладают сглаживающим свойством, при их использовании в качестве базиса для кодирования сигналов.

 Вейвлет-анализ является одним из наиболее мощных и гибких средств исследования как одномерных, так и двумерных сигналов. Так, в работе [9] вейвлет-преобразование служит для анализа поверхностей методом проекционных полос с учетом возникающих дифракционных пятен. Также вейвлет-преобразование способствует в работе [10] определению экономического влияния COVID-19 на производство США. В работе [11] рассматривается вопрос существования решения интегрального уравнения Фредгольма с использованием сразу нескольких вейвлетов. Помимо этого, вейвлет-преобразование широко применяется в хроматографии и спектрометрии, к примеру, в работе [12] данное преобразование позволяет авторам дешево, быстро и точно определять содержание дорзоламида и тимолола в человеческой слезе, при этом используется множество различных вейвлетов одновременно.

Вейвлет-преобразование, при использовании множества вейвлетов одновременно, из-за необходимости осуществлять интегрирование зачастую вызывает затруднение при анализе сигналов произвольной формы, что и составляет рассматриваемую в данной работе научную проблему. Следовательно, для разработки современных алгоритмов обработки сигналов и решения уравнений актуальным является вопрос вычисления вейвлет-преобразования сигналов произвольной формы без необходимости интегрирования. В соответствии с этим, задачей настоящего исследования является формирование быстрого вычислительного алгоритма рекуррентного вычисления вейвлет-преобразования сигналов без интегрирования с применением методики кодирования в базисе функций Чебышева-Эрмита.

Базис перехода от коэффициентов разложения по функциям Чебышева-Эрмита к вейвлет-преобразованию

Ранее, в работе [4] была рассмотрена возможность перехода от коэффициентов  кодирования сигнала в базисе функций Чебышева-Эрмита к вейвлет-преобразованию  этого сигнала при использовании в качестве вейвлета производной функции Гаусса m порядка (далее вейвлет-преобразование m порядка). Если сигнал , закодированный в базисе функций  по  функциям (при ) можно восстановить по выражению:

       (1)

где x₀ - величина сдвига функции Чебышева-Эрмита;

γ - коэффициент масштаба функции Чебышева-Эрмита;

то для восстановления вейвлет-преобразования  сигнала  m порядка можно прибегнуть к подобному (1) выражению, в котором  сменяются на функции  базиса перехода к вейвлет-преобразованию:

      (2)

где a – коэффициент масштаба вейвлета;

b – коэффициент сдвига вейвлета;

и сам базис записывается следующим образом:

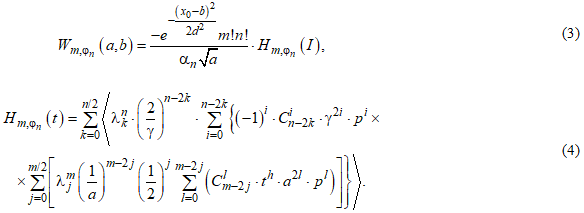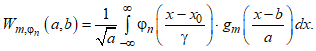где . Базис (3) получен путем интегрирования произведения n-й базисной функции и вейвлета m порядка:       (5)

Нетрудно заметить, что расчет (4) при высоких порядках m и n затруднителен в силу большого количества математических операций. Следовательно, и сам базис перехода к вейвлет-преобразованию (3) будет требовать все больше времени при увеличении числа используемых базисных функций, либо с увеличением порядка вейвлета. Следовательно, для эффективного применения базиса требуется сократить количество вычислительных процедур.

Формирование рекуррентного представления базиса перехода от коэффициентов разложения по функциям Чебышева-Эрмита к вейвлет-преобразованию

Одним из очевидных способов упростить расчет полинома (4) является его преобразование к рекуррентной форме, что априори возможно, поскольку известны рекуррентные формулы для составляющих данное выражение многочленов Эрмита [9]:

 

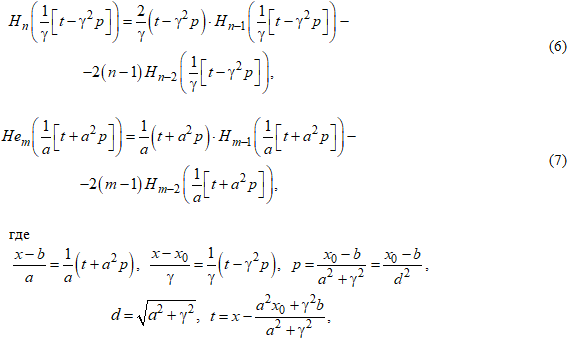
- замены, введенные в [4] для упрощения интегрирования.

Для перехода (3) к рекуррентному представлению следует найти произведение (6) и (7). Обозначив данное произведение , а также, для упрощения записи, введя обозначения  и  получим, после раскрытия скобок и приведения подобных членов:

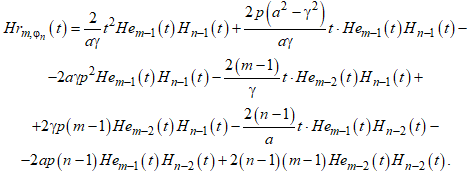         (8)

Поскольку каждый член (8) представляет собой, равно как и само выражение (8), произведение , допускается ввести также для каждого члена (8) обозначение

Поскольку полином (8) находится под знаком интеграла при расчете вейвлет-преобразования (5), для упрощения интегрирования, за счет дистрибутивности суммы, следует внести множитель t под знак суммы и привести все множители t с различными степенями к одному основанию. Выполнив данные преобразования возможно совершить в выражении выше замену , которой соответствует табличный интеграл [10]:

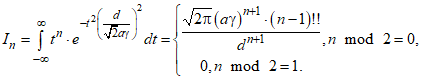      (9)

Данная замена необходима [4] для интегрирования в (5).

Чтобы упростить дальнейшую запись выражений, введем следующее обозначение для полинома с внесенным под знак суммы множителем t:

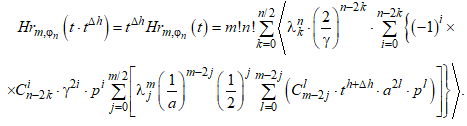      (10)

Очевидно, правая часть (10) представляет собой  со степенью t под знаком суммы, соответствующей выбранным m, n, к котором добавляется степень множителя . В соответствии с (10) можно выполнить замену в (8), получив при этом:

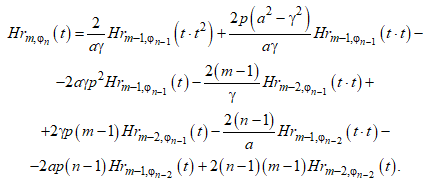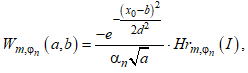        (11) Подставляя  в (3) вместо  с соответствующей заменой  получим:         (12)

при этом, следуя терминологии, введенной в (11), в дальнейшем можно обозначать , при этом, аналогично (10), в явном виде такое обозначение будет иметь следующий смысл:

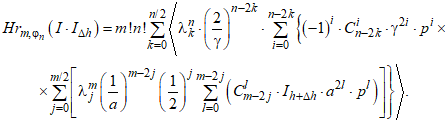      (13)

Сформировать из (12) рекуррентную формулу можно, если подставить в него выражение (11), раскрыть скобки и выделить в виде (12) все возможные отдельные :

 

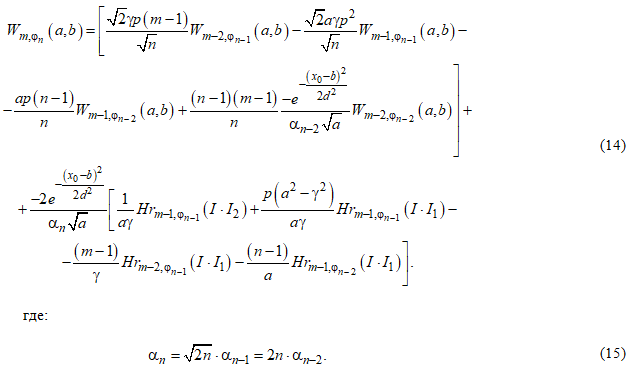
Полученное выражение (14) хоть и ссылается на собственные члены низших порядков, но содержит также четыре члена , которые невозможно свести к виду (14), поэтому каждый из данных членов должен быть рассчитан отдельно, также рекуррентно, согласно выражению (11). За счет этого теряются преимущества в скорости вычислений, при этом запись базиса в виде (14) куда более громоздкая по сравнению с (12). Поскольку целью перехода к рекуррентной форме являлось упрощение вычислительного процесса, наиболее оптимальным способом формирования базиса перехода к вейвлет-преобразованию с вейвлетами-производными функции Гаусса, является предварительный расчет полиномов (11) рекуррентно с последующей подстановкой результата в (12).

Заключение

Таким образом, в качестве результата работы выступают выражения (14) и (15) задающие искомые выражения рекуррентного вычисления без интегрирования множества вейвлет-преобразований сигнала, закодированного в базисе функций Чебышева-Эрмита. Полученные выражения основываются на рекуррентных свойствах полиномов Эрмита, из-за чего, при предварительном вычислении всех требуемых начальных членов выражения (14), становится возможным без интегрирования сформировать вейвлет-коэффициенты исследуемого сигнала по целому семейству вейвлетов, заданных производной функции Гаусса, к которым, в частности, относится и широко распространенный вейвлет «Мексиканская шляпа».

Финансирование Работа выполнена при финансовой поддержке гранта аспирантов ФГБОУ ВО «СамГТУ».	Funding The paper is carried out with financial support of SamSTU’s postgraduate student grant.
Конфликт интересов Не указан.	Conflict of Interest None declared.

Список литературы / References

1. Сайфуллин Р.Т. Выбор необходимого числа базисных функций в алгоритмах кодирования-декодирования сигналов аналитических приборов / Р.Т. Сайфуллин, А.В. Бочкарев // Информационно-измерительные и управляющие системы: межвуз. сб. науч. статей. Выпуск 1(17). – 2019, с. 35-42
2. Сайфуллин Р.Т. Вычисление производных аналитического сигнала в базисе функций Чебышева-Эрмита. / Р.Т. Сайфуллин, А.В. Бочкарев // Материалы XI Всероссийской научной конференции с международным участием «Математическое моделирование и краевые задачи» (27–30 мая 2019 г., Самара, Россия). Том 2. – 2019, с. 137-139
3. Сайфуллин Р.Т. Вычисление непрерывного вейвлет-преобразования сигналов в базисе функций Чебышева-Эрмита. / Р.Т. Сайфуллин, А.В. Бочкарев // Вестник Самарского государственного технического университета. Серия: технические науки, № 2(62). – 2019, с. 99-113
4. Сайфуллин Р.Т. Алгоритм вычисления коэффициентов вейвлет-преобразования сигналов с использованием базиса функций Чебышева-Эрмита. / Р.Т. Сайфуллин, А.В. Бочкарев // Вестник Самарского государственного технического университета. Серия: технические науки, № 4(64). – 2019, с. 113-124
5. Xue Luo. Spectral viscosity method with generalized Hermite functions for nonlinear conservation laws / Xue Luo. // Applied Numerical Mathematics, Volume 123, 2018. P. 256-274.
6. Рогазинский С. В. Рандомизированный проекционный метод для решения нелинейного уравнения Больцмана в трехмерном случае / С. В. Рогазинский // Марчуковские научные чтения, №2020. – 2020, c. 51.
7. Rogasinsky S.V. Two variants of Monte Carlo projection method for numerical solution of nonlinear Boltzmann equation / S. V.Sergey // Russ. J. Numer. Anal. Math. Modelling, Volume 34, Issue 3 (Jun 2019).
8. Балакин Д.А. Построение ортогонального банка фильтров на основе преобразований Эрмита для обработки сигналов. / Д.А. Балакин, В.В. Штыков // Журнал радиоэлектроники, №9, 2014, с. 1-15.
9. Shang W. Analysis and reduction of error caused by tested object using fringe projection technique with wavelet transform. / W. Shang, S. Liu, J. Wang, R. Shao. // Optik, Vol. 221, 2020.
10. Choi S.-Y. Industry volatility and economic uncertainty due to the COVID-19 pandemic: Evidence from wavelet coherence analysis / S.-Y. Choi // Finance Research Letters, Vol. 37, 2020.
11. Rabbani M. Compact operators for existence of solution and projection method with multi-wavelet bases to solve (F.IES) and error analysis in Sobolev space. / M. Rabbani // Journal of Computational and Applied Mathematics, Vol. 382, 2021
12. Valizadeh M. The application of continuous wavelet transform based on spectrophotometric method and high-performance liquid chromatography for simultaneous determination of anti-glaucoma drugs in eye drop. / M. Valizadeh, M.R. Sohrabi, F. Motiee. // Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy, Vol. 242, 2020.
13. Szego G. Orthogonal Polynomials: 4^th ed. / G. Szego, Rhode Island: American Mathematical Society, 2003, – 432 p.
14. Градштейн И.С. Таблицы интегралов, сумм, рядов и произведений / И.С. Градштейн, И.М. Рыжик. – М.: Физматгиз, 1963, – 1100 с.

Список литературы на английском языке / References in English

1. Sajfullin R.T. Vybor neobhodimogo chisla bazisnyh funkcij v algoritmah kodirovanija-dekodirovanija signalov analiticheskih priborov. [The choice of the required number of basis functions in the algorithms for coding and decoding signals of analytical instruments] / R.T. Sajfullin, A.V. Bochkarev // Informacionno-izmeritel'nye i upravljajushhie sistemy: mezhvuz. sb. nauch. statej. [Information-measuring and control systems: interuniversity collection of scientific papers] № 1(17). – 2019, p. 35-42 [in Russian]
2. Sajfullin R.T. Vychislenie proizvodnyh analiticheskogo signala v bazise funkcij Chebysheva-Jermita. [Calculation of the derivatives of the analytical signal in the basis of the Chebyshev-Hermite functions] / R.T. Sajfullin, A.V. Bochkarev // Materialy XI Vserossijskoj nauchnoj konferencii s mezhdunarodnym uchastiem «Matematicheskoe modelirovanie i kraevye zadachi» [Mathematical modeling and boundary value problems] (27–30 may 2019, Samara, Russia). Vol. 2. – 2019, p. 137-139 [in Russian]
3. Sajfullin R.T. Vychislenie nepreryvnogo vejvlet-preobrazovanija signalov v bazise funkcij Chebysheva-Jermita. [Calculation of continuous wavelet transform of signals in the basis of Chebyshev-Hermite functions] / R.T. Sajfullin, A.V. Bochkarev // Vestnik Samarskogo gosudarstvennogo tehnicheskogo universiteta. Serija: tehnicheskie nauki [Bulletin of the Samara State Technical University. Series: technical sciences], № 2(62). – 2019, pp. 99-113 [in Russian]
4. Sajfullin R.T. Algoritm vychislenija kojefficientov vejvlet-preobrazovanija signalov s ispol'zovaniem bazisa funkcij Chebysheva-Jermita. [Calculation of continuous wavelet transform of signals in the basis of Chebyshev-Hermite functions] / R.T. Sajfullin, A.V. Bochkarev // Vestnik Samarskogo gosudarstvennogo tehnicheskogo universiteta. Serija: tehnicheskie nauki [Bulletin of the Samara State Technical University. Series: technical sciences], № 4(64). – 2019, pp. 113-124 [in Russian]
5. Xue Luo. Spectral viscosity method with generalized Hermite functions for nonlinear conservation laws / Xue Luo. // Applied Numerical Mathematics, Volume 123, 2018. P. 256-274.
6. Rogazinskij S.V. Randomizirovannyj proekcionnyj metod dlja reshenija nelinejnogo uravnenija Bol'cmana v trehmernom sluchae [A randomized projection method for solving the nonlinear Boltzmann equation in the three-dimensional case] / S.V. Rogazinskij // Marchukovskie nauchnye chtenija [Marchuk Scientific Readings], № 2020. – 2020, p. 51 [in Russian]
7. Rogasinsky S.V. Two variants of Monte Carlo projection method for numerical solution of nonlinear Boltzmann equation / S.V. Rogazinskij // Russ. J. Numer. Anal. Math. Modelling, Volume 34, Issue 3 (Jun 2019).
8. Balakin D.A. Postroenie ortogonal'nogo banka fil'trov na osnove preobrazovanij Jermita dlja obrabotki signalov. [Construction of an orthogonal filter bank based on Hermite transforms for signal processing] / D.A. Balakin, V.V. Shtykov // Zhurnal radiojelektroniki [Radioelectronics Journal], №9, 2014, pp. 1-15 [in Russian]
9. Shang W. Analysis and reduction of error caused by tested object using fringe projection technique with wavelet transform. / W. Shang, S. Liu, J. Wang, R. Shao. // Optik, Vol. 221, 2020.
10. Choi S.-Y. Industry volatility and economic uncertainty due to the COVID-19 pandemic: Evidence from wavelet coherence analysis / S.-Y. Choi // Finance Research Letters, Vol. 37, 2020.
11. Rabbani M. Compact operators for existence of solution and projection method with multi-wavelet bases to solve (F.IES) and error analysis in Sobolev space. / M. Rabbani // Journal of Computational and Applied Mathematics, Vol. 382, 2021
12. Valizadeh M. The application of continuous wavelet transform based on spectrophotometric method and high-performance liquid chromatography for simultaneous determination of anti-glaucoma drugs in eye drop. / M. Valizadeh, M.R. Sohrabi, F. Motiee. // Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy, Vol. 242, 2020.
13. Szego G. Orthogonal Polynomials: 4^th ed. / G. Szego, Rhode Island: American Mathematical Society, 2003, – 432 p.
14. Gradshtejn I.S. Tablicy integralov, summ, rjadov i proizvedenij. [Integral, sums, series and multiplies tables] / I.S. Gradshtejn, I.M. Ryzhik. – M.: Fizmatgiz, 1963, – 1100 p. [in Russian]