ВЛИЯНИЕ ВХОДНЫХ ОСЦИЛЛЯЦИЙ НА ПОВЕДЕНИЕ СПАЙКОВОЙ СЕТИ РАБОЧЕЙ ПАМЯТИ
ВЛИЯНИЕ ВХОДНЫХ ОСЦИЛЛЯЦИЙ НА ПОВЕДЕНИЕ СПАЙКОВОЙ СЕТИ РАБОЧЕЙ ПАМЯТИ
Научная статья
Водорезова К.Г.1, Новиков Н.А.2, *, Гуткин Б.С.3
1 ORCID: 0000-0003-3518-2572;
2 ORCID: 0000-0003-4643-5491;
3 ORCID: 0000-0001-6409-979X;
1, 2, 3 Центр нейроэкономики и когнитивных исследований, Национальный исследовательский университет «Высшая школа экономики», Москва, Россия;
3 Группа изучения нейрональной теории, Департамент когнитивных исследований, Высшая нормальная школа, Париж, Франция
* Корреспондирующий автор (nikknovikov[at]gmail.com)
АннотацияРабочая память является способностью мозга к кратковременному удержанию информации, необходимой для решения текущей задачи. В период удержания наблюдается повышение активности отдельных нейронов, а также изменения осцилляторной активности мозга. Данное исследование посвящено изучению влияния входных осцилляций на модель рабочей памяти, представленную бистабильной тормозно-возбуждающей спайковой нейронной сетью. Мы разработали усовершенствованный метод самосогласованного поля, основанный на предвычислении значений функций отклика нейронов при различных сочетаниях среднего входа, силы шума и амплитуды входных осцилляций. Используя данный метод, мы построили модель, в которой входные колебания приводят к более выраженному повышению среднего уровня активности в том случае, когда сеть рабочей памяти находится в состоянии удержания объекта, по сравнению с фоновым состоянием. Предсказания, полученные на основе разработанного метода, оказались в хорошем соответствии с численными симуляциями модели. Мы предполагаем, что предложенный нами механизм может служить основой для стабилизации состояния сетей рабочей памяти при помощи осцилляторного воздействия со стороны мозговых структур, осуществляющих контроль над выполнением текущих задач.
Ключевые слова: рабочая память, спайковые сети, бистабильность, вынужденные колебания, метод самосогласованного поля.
INFLUENCE OF INPUT OSCILLATIONS ON BEHAVIOR OF SPIKING NETWORK OF WORKING MEMORY
Research article
Vodorezova K.G.1, Novikov N.A.2*, Gutkin B.S.3
1 ORCID: 0000-0003-3518-2572;
2 ORCID: 0000-0003-4643-5491;
3 ORCID: 0000-0001-6409-979X;
1, 2, 3 Center for Neuroeconomics and Cognitive Research, National Research University, Higher School of Economics, Moscow, Russia;
3 Neuronal Theory Studying Group, Department of Cognitive Research, Higher Normal School, Paris, France
* Corresponding author (nikknovikov[at]gmail.com)
AbstractWorking memory is the ability of a brain to briefly hold the information necessary to solve some current problem. The increase in the activity of individual neurons, as well as changes in the oscillatory activity of a brain, is observed during the retention period. This study is devoted to studying the influence of input oscillations on the working memory model represented by a bistable inhibitory-stimulating spiking neural network. We have developed an improved method of self-consistent field, based on the pre-calculation of the values of the response functions of neurons for various combinations of the average input, noise power, and amplitude of the input oscillations. Using this method, we have built a model in which input fluctuations lead to a more pronounced increase in the average level of activity when the network of working memory is in a state of holding the object, compared with the background state. Predictions obtained on the basis of the developed method turned out to be in good agreement with numerical simulations of the model. We assume that the mechanism we have proposed can serve as the basis for stabilizing the state of working memory networks using oscillatory action from the side of brain structures that monitor the implementation of current tasks.
Keywords: working memory, spiking networks, bistability, forced oscillations, self-consistent field method.
ВведениеРабочая память (РП) - это нейрокогнитивный конструкт, обеспечивающий одновременное удержание и обработку информации, релевантной к выполняемому в данный момент заданию, но не воспринимаемой непосредственно органами чувств в период удержания [1]. РП может хранить ограниченное число ментальных репрезентаций в течение непродолжительного времени.
Типичная задача, используемая для изучения РП, устроена следующим образом: вначале испытуемому предъявляется один или несколько стимулов, после чего следует период удержания (обычно – несколько секунд), за которым следует тестовая фаза. В тестовой фазе испытуемый должен совершить реакцию, правильность которой требует использования информации об удерживаемых в памяти стимулах.
Электрофизиологические записи нейронов префронтальной коры приматов указывают на наличие нейронов, которые генерируют спайки с повышенной частотой в течение всего периода удержания [2], [3]. Данное явление носит название самоподдерживающейся активности; считается, что такая активность является одним из основных механизмов, лежащих в основе явления РП. Помимо префронтальной коры, самоподдерживающаяся активность была обнаружена в ряде других областей мозга [4], [5], [6].
Общим свойством большинства моделей РП является бистабильность, т.е. сосуществование двух режимов активности – фонового и активного, которым соответствуют различные значения частоты спайков. В фоновом состоянии моделируемая сеть нейронов не участвует в удержании какого-либо стимула и обладает низкой частотой спайков. Стимул для запоминания моделируется в виде короткого возбуждающего импульса, подаваемого на вход сети; этот импульс переводит сеть из фонового в активное состояние. В активном состоянии сеть генерирует спайки с повышенной частотой, что соответствует экспериментально наблюдаемой самоподдерживающейся активности, являющейся нейрокоррелятом активного удержания стимула в РП. Модель РП на основе бистабильной спайковой сети (состоящей из возбуждающих и тормозных нейронов типа “интегратор с утечкой”) впервые была представлена в работе [7].
Помимо повышения активности отдельных нейронов в период удержания, экспериментально также наблюдаются изменения в характере коллективной осцилляторной активности нейрональных популяций. Наибольший интерес представляет усиление колебаний в бета-диапазоне (14-35 Гц) в период удержания [8], [9], [10]. Существует гипотеза о том, что мозговые осцилляции в бета-диапазоне стабилизируют текущее состояние сетей нейронов и препятствуют его изменению, т.е. обеспечивают «статус-кво» [11]. Частным случаем поддержания статуса-кво является удержание информации в рабочей памяти.
Несмотря на многолетние исследования, функциональная роль осцилляций в осуществлении функций рабочей памяти остается до конца не выясненной. Существует ряд теоретических работ, посвященных как роли биофизических механизмов генерации бета-ритма в поддержании рабочей памяти [12], так и изучению более общих механизмов взаимосвязи осцилляций с функциями рабочей памяти [13], [14], [15]. Однако, в целом, теоретическое осмысление данного вопроса носит несистематизированный характер.
Предлагаемая нами гипотеза относительно стабилизирующей роли бета-осцилляций заключается в следующем. Мы можем предположить наличие неспецифических источников осцилляций (например, в глубоких слоях коры или в базальных ядрах), которые поступают на вход бистабильных популяций поверхностных слоев коры, реализующих функции РП. Популяции, находящиеся в активном состоянии (т.е. непосредственно удерживающие информацию в РП) демонстрируют более сильные вызванные колебания по сравнению с популяциями, находящимися в фоновом состоянии. Вызванные колебания могут приводить к повышению средней частоты генерации спайков за счет нелинейного характера функционирования нейронов. Таким образом, «включение» осцилляторного входа в поверхностные слои коры может приводить к дополнительному возбуждению активных, но не фоновых, популяций; за счет этого существующее распределение активности по популяциям становится более устойчивым.
В данной работе мы предлагаем метод получисленного предсказания сдвига среднего уровня активности популяции под действием входных осцилляций. Мы показываем, что при определенных параметрах модели этот сдвиг оказывается больше в активном состоянии, чем в фоновом. Также мы подтверждаем данное предсказание непосредственной симуляцией соответствующей спайковой сети.
Методы и принципы исследования
Модель
Наша модель представляет собой сеть из ![]() возбуждающих и
возбуждающих и ![]() тормозных нейронов типа «интегратор с утечкой» (leaky integrate-and-fire, LIF). Каждый нейрон получает
тормозных нейронов типа «интегратор с утечкой» (leaky integrate-and-fire, LIF). Каждый нейрон получает ![]() возбуждающих и
возбуждающих и ![]() тормозных входов (
тормозных входов (![]() ). Возбуждение опосредовано через мгновенные AMPA-рецепторы и медленные NMDA-рецепторы; торможение опосредовано через мгновенные GABAA-рецепторы. Помимо рекуррентных входов, нейроны получают внешний вход (со стороны частей мозга, не входящих непосредственно в модель). Внешний вход состоит из постоянной составляющей, гауссовского белого шума и синусоидальных колебаний с нулевым средним. Формально, модель описывается следующей системой уравнений:
). Возбуждение опосредовано через мгновенные AMPA-рецепторы и медленные NMDA-рецепторы; торможение опосредовано через мгновенные GABAA-рецепторы. Помимо рекуррентных входов, нейроны получают внешний вход (со стороны частей мозга, не входящих непосредственно в модель). Внешний вход состоит из постоянной составляющей, гауссовского белого шума и синусоидальных колебаний с нулевым средним. Формально, модель описывается следующей системой уравнений:
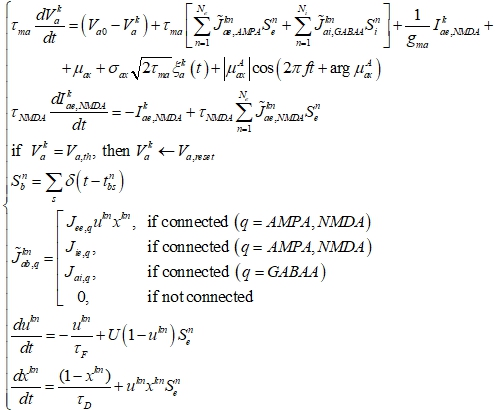 (1)
(1)
где индексы ![]() обозначают тип популяции, к которой относится постсинаптический и пресинаптический нейроны, соответственно (
обозначают тип популяции, к которой относится постсинаптический и пресинаптический нейроны, соответственно (![]() , e – возбуждающая, i – тормозная); k – индекс постсинаптического нейрона, n - индекс пресинаптического нейрона; s – индекс спайка; q – тип рецептора (AMPA / NMDA / GABAA);
, e – возбуждающая, i – тормозная); k – индекс постсинаптического нейрона, n - индекс пресинаптического нейрона; s – индекс спайка; q – тип рецептора (AMPA / NMDA / GABAA); ![]() – количество нейронов в популяции b;
– количество нейронов в популяции b; ![]() – мембранный потенциал k-го нейрона популяции a,
– мембранный потенциал k-го нейрона популяции a, ![]() – входной ток через NMDA-рецепторы для данного нейрона;
– входной ток через NMDA-рецепторы для данного нейрона; ![]() – мембранная константа, проводимость мембраны и потенциал покоя нейронов из популяции a, соответственно;
– мембранная константа, проводимость мембраны и потенциал покоя нейронов из популяции a, соответственно; ![]() – порог генерации спайков и напряжение перезагрузки, соответственно;
– порог генерации спайков и напряжение перезагрузки, соответственно; ![]() – временная константа NMDA-рецепторов;
– временная константа NMDA-рецепторов; ![]() – момент генерации s-го спайка n-м нейроном популяции b;
– момент генерации s-го спайка n-м нейроном популяции b; ![]() – серия спайков, генерируемых n-м нейроном популяции b;
– серия спайков, генерируемых n-м нейроном популяции b; ![]() – вес связи из n-го нейрона популяции b в k-й нейрон популяции a через рецепторы типа q;
– вес связи из n-го нейрона популяции b в k-й нейрон популяции a через рецепторы типа q; ![]() - вес связей из нейронов популяции b в нейроны популяции a через рецепторы типа q (одинаковый для всех пар нейронов данных популяций, между которыми есть физическая связь);
- вес связей из нейронов популяции b в нейроны популяции a через рецепторы типа q (одинаковый для всех пар нейронов данных популяций, между которыми есть физическая связь); ![]() – среднее входное напряжение,
– среднее входное напряжение, ![]() – стандартное отклонение входного напряжения,
– стандартное отклонение входного напряжения, ![]() – гауссовский белый шум с нулевым средним и единичной дисперсией (генерируемый независимо для каждого нейрона;
– гауссовский белый шум с нулевым средним и единичной дисперсией (генерируемый независимо для каждого нейрона; ![]() – амплитуда, частота и фаза входных осцилляций, соответственно;
– амплитуда, частота и фаза входных осцилляций, соответственно; ![]() – переменные, описывающие кратковременную пластичность связи из n-го в k-й нейрон возбуждающей популяции;
– переменные, описывающие кратковременную пластичность связи из n-го в k-й нейрон возбуждающей популяции; ![]() – временные константы синаптической фасилитации и депрессии, соответственно; U – константа, характеризующая соотношение между синаптической фасилитацией и депрессией.
– временные константы синаптической фасилитации и депрессии, соответственно; U – константа, характеризующая соотношение между синаптической фасилитацией и депрессией.
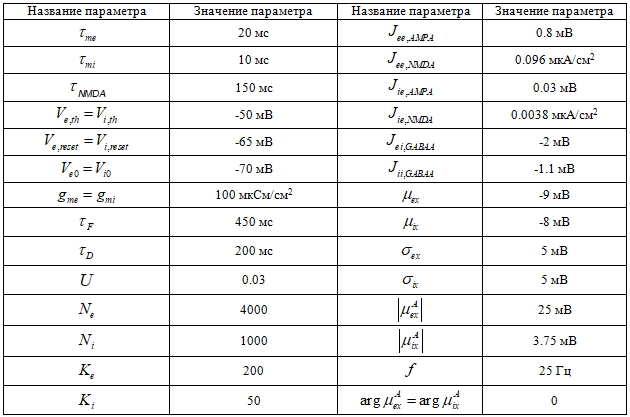
Параметры модели приведены в Таблице 1. Численная симуляция модели осуществлялась при помощи библиотеки Brian, шаг симуляции составлял 0.1 мс.
Таблица 1 – Параметры симуляции спайковой сети
Предвычисление передаточных функций
Разработанный нами метод полуаналитического предсказания положений равновесия требует знания зависимости средней частоты спайков, генерируемых нейроном, от параметров входного сигнала: среднего значения μ и стандартного отклонения σ стационарной составляющей, а также амплитуды ![]() осцилляторной составляющей. Для определения этой зависимости мы провели симуляцию изолированного нейрона (отдельно для возбуждающего и отдельно для тормозного нейрона) при различных комбинациях
осцилляторной составляющей. Для определения этой зависимости мы провели симуляцию изолированного нейрона (отдельно для возбуждающего и отдельно для тормозного нейрона) при различных комбинациях ![]() :
:
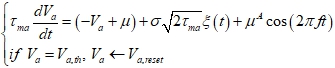 (2)
(2)
где ![]() – мембранный потенциал;
– мембранный потенциал; ![]() – гауссовский белый шум с нулевым средним и единичной дисперсией.
– гауссовский белый шум с нулевым средним и единичной дисперсией.
Комбинации (![]() ) выбирались в узлах трехмерной прямоугольной сетки; для каждой комбинации на основе результатов симуляции определялась средняя частота спайков
) выбирались в узлах трехмерной прямоугольной сетки; для каждой комбинации на основе результатов симуляции определялась средняя частота спайков ![]() (
(![]() ). Данная процедура, требующая много вычислительного времени, проводилась однократно. В ходе дальнейшего анализа, значения частоты спайков определялись для произвольных комбинаций
). Данная процедура, требующая много вычислительного времени, проводилась однократно. В ходе дальнейшего анализа, значения частоты спайков определялись для произвольных комбинаций ![]() (
(![]() ) при помощи кубической интерполяции между предвычисленными значениями
) при помощи кубической интерполяции между предвычисленными значениями ![]() , хранящимися в ближайших узлах сетки.
, хранящимися в ближайших узлах сетки.
Анализ самосогласованности
Для каждой комбинации (![]() ), взятой из узлов некоторой прямоугольной сетки, мы вычисляли средние значения
), взятой из узлов некоторой прямоугольной сетки, мы вычисляли средние значения ![]() и стандартные отклонения
и стандартные отклонения ![]() стационарной части входных сигналов, получаемых нейронами:
стационарной части входных сигналов, получаемых нейронами:
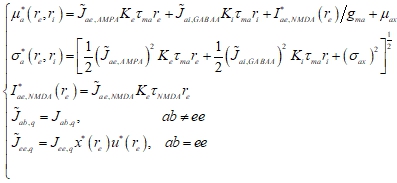 (3)
(3)
где ![]() – синаптический вес с учетом кратковременной пластичности;
– синаптический вес с учетом кратковременной пластичности; ![]() – равновесное значение NMDA-тока;
– равновесное значение NMDA-тока; ![]() – равновесные значения переменных x и u для синапса, получающего на вход пуассоновскую серию спайков с частотой
– равновесные значения переменных x и u для синапса, получающего на вход пуассоновскую серию спайков с частотой ![]() . Мы полагали, что дисперсия входа, создаваемая током через медленные NMDA-рецепторы, пренебрежимо мала.
. Мы полагали, что дисперсия входа, создаваемая током через медленные NMDA-рецепторы, пренебрежимо мала.
Кроме того, для каждой комбинации (![]() ) мы вычисляли комплекснозначные амплитуды вынужденных колебаний популяционных частот
) мы вычисляли комплекснозначные амплитуды вынужденных колебаний популяционных частот ![]() и средних суммарных входных сигналов, получаемых нейронами
и средних суммарных входных сигналов, получаемых нейронами ![]() . Для этого мы решали следующую систему уравнений:
. Для этого мы решали следующую систему уравнений:
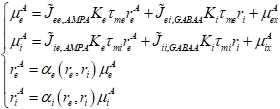 (4)
(4)
где ![]() – коэффициенты линейной связи между амплитудой колебаний входа и амплитудой колебаний частоты спайков, зависящие от средних частот спайков
– коэффициенты линейной связи между амплитудой колебаний входа и амплитудой колебаний частоты спайков, зависящие от средних частот спайков ![]() и вычисляемые в соответствии с формулой, приведенной в статье [16]. Мы полагали, что влияние осцилляций на медленный NMDA-ток пренебрежимо мало.
и вычисляемые в соответствии с формулой, приведенной в статье [16]. Мы полагали, что влияние осцилляций на медленный NMDA-ток пренебрежимо мало.
Затем мы определяли линии на фазовой плоскости, соответствующие условиям:
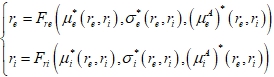 (5)
(5)
В случае отсутствия внешних колебаний (![]() ), данные линии представляют собой нульклины невозмущенной системы (1), а точки их пересечения – неподвижные точки невозмущенной системы. При наличии внешних колебаний, пересечения линий можно рассматривать как неподвижные точки периодически возмущенной системы (1), усредненной по времени. Разработанный нами метод является развитием метода самосогласованного поля; его новизна заключается в возможности учета влияния периодического возмущения на усредненное по времени состояние системы.
), данные линии представляют собой нульклины невозмущенной системы (1), а точки их пересечения – неподвижные точки невозмущенной системы. При наличии внешних колебаний, пересечения линий можно рассматривать как неподвижные точки периодически возмущенной системы (1), усредненной по времени. Разработанный нами метод является развитием метода самосогласованного поля; его новизна заключается в возможности учета влияния периодического возмущения на усредненное по времени состояние системы.
Основные результаты
Используя разработанный нами вариант метода самосогласованного поля, мы выбрали параметры системы, удовлетворяющие следующим критериям: (а) невозмущенная система и усредненная по времени невозмущенная система являются бистабильными, (б) периодическое возмущение приводит к более выраженному сдвигу средней частоты спайков возбуждающей популяции ![]() для активного состояния, по сравнению с фоновым состоянием. На Рисунке 1 представлена фазовая плоскость (
для активного состояния, по сравнению с фоновым состоянием. На Рисунке 1 представлена фазовая плоскость (![]() ) с нульклинами и положениями равновесия для невозмущенной системы и для периодически возмущенной системы, усредненной по времени. Видно, что расстояние по оси
) с нульклинами и положениями равновесия для невозмущенной системы и для периодически возмущенной системы, усредненной по времени. Видно, что расстояние по оси ![]() между возмущенным и невозмущенным положением равновесия больше для активного состояния (в правой части рисунка), чем для фонового состояния (в левой части рисунка).
между возмущенным и невозмущенным положением равновесия больше для активного состояния (в правой части рисунка), чем для фонового состояния (в левой части рисунка).
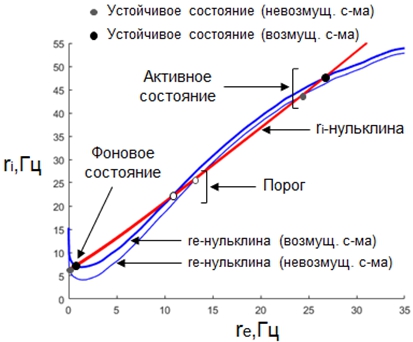
Рис. 1 – Фазовая плоскость (![]() ).
).
Примечание: Тонкая синяя линия – ![]() -нульклина невозмущенной системы; толстая синяя линия –
-нульклина невозмущенной системы; толстая синяя линия – ![]() -нульклина усредненной по времени возмущенной системы; красная линия –
-нульклина усредненной по времени возмущенной системы; красная линия – ![]() -нульклина
-нульклина
Пересечения ![]() - и
- и ![]() -нульклин соответствуют неподвижным точкам соответствующих систем. Пересечения в левой части рисунка – фоновое равновесие; в правой части рисунка – состояние активного удержания информации в РП; в средней части рисунка – порог перехода между фоновым и активным состоянием.
-нульклин соответствуют неподвижным точкам соответствующих систем. Пересечения в левой части рисунка – фоновое равновесие; в правой части рисунка – состояние активного удержания информации в РП; в средней части рисунка – порог перехода между фоновым и активным состоянием.
Результаты симуляции спайковой сети представлены на Рисунке 2. На панели б) представлена симуляция сети, находящейся в фоновом состоянии. На панели а) представлена симуляция сети, которая переводится из фонового в активное состояние при помощи входного возбуждающего импульса (300 – 1500 мс). Видно, что после короткого переходного периода, следующего за окончанием импульса, сеть выходит в активное состояние и остается в нем. Сопоставление поведения сети на панелях а) и б) в интервале 2000 – 4000 мс подтверждает, что сеть является бистабильной, причем положения равновесия соответствуют предсказанным на основе анализа самосогласованности (см. Рисунок 1, невозмущенные положения равновесия).
После 4000 мс на вход сети подавались синусоидальные колебания в бета-диапазоне. Из Рисунка 2 видно, что вызываемый входными колебаниями сдвиг средней частоты спайков возбуждающей популяции больше для сети, находящейся в активном состоянии (3 Гц), по сравнению с сетью в фоновом состоянии (0.4 Гц). Полученные результаты соответствуют предсказаниям, полученным при помощи усовершенствованного нами анализа самосогласованности (см. Рисунок 1, расстояния между возмущенными и невозмущенными положениями равновесия).
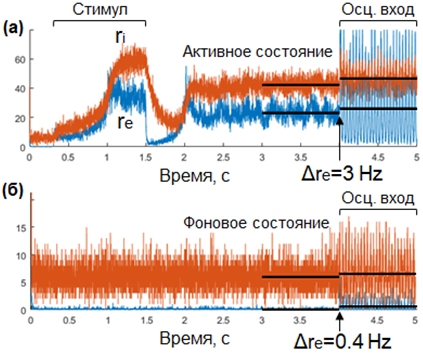
Рис. 2 – Результаты симуляции спайковой сети
Примечание: синие линии – частота спайков возбуждающей популяции, красные линии – частота спайков тормозной популяции. Черными горизонтальными линиями показаны средние популяционные частоты в течение секунды до и после включения входных осцилляций. (а) Сеть переводится в активное состояние при помощи возбуждающего импульса, (б) сеть находится в фоновом состоянии
Заключение
Изучение роли нейрональных осцилляций в реализации функций рабочей памяти (РП) является актуальной темой исследований, а теоретическое осмысление этой роли далеко от завершения. В данной работе мы предложили возможный механизм стабилизации РП, основанный на селективном повышении уровня активности репрезентаций удерживаемых в памяти объектов при помощи входных осцилляций. При этом подача аналогичных осцилляций на вход популяций, находящихся в фоновом состоянии (т.е. не участвующих в удержании информации в РП), не приводит к значимому повышению активности. Такая селективность обеспечивается за счет различия в резонансных свойствах между фоновым состоянием и состоянием активного удержания следа памяти. Предложенный механизм позволяет контролировать устойчивость РП при помощи осцилляций из источника, который сам по себе может не содержать информации о содержимом РП; иными словами, обеспечивается разделение буфера памяти и контроллера ее устойчивости.
В ходе исследования мы разработали новый метод предсказания поведения спайковой сети с осцилляторным входом, основанный на усовершенствованном анализе самосогласованности. Предсказания, полученные данным методом, показали хорошее соответствие результатам численной симуляции спайковой сети. В будущем, разработанный нами метод может быть применен для исследования более общих случаев, таких как поведение мультиобъектной модели рабочей памяти, основанной на системе нескольких конкурирующих бистабильных сетей, связанных реципрокным торможением.
| Финансирование Работа была выполнена при поддержке гранта Российского Научного Фонда (договор №: 17-11-01273). | Funding The research was supported by a Russian Science Foundation grant (contract No: 17-11-01273). |
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Baddeley A. Working memory: Looking back and looking forward / A. Baddeley // Nature Reviews Neuroscience. — 2003. — Vol. 4, № 10. — P. 829–839.
- Funahashi S. Mnemonic coding of visual space in the monkey’s dorsolateral prefrontal cortex / S. Funahashi, C.J. Bruce, P.S. Goldman-Rakic // Journal of Neurophysiology. — 1989. — Vol. 61, № 2. — P. 331–349.
- Goldman-Rakic P.S. Cellular basis of working memory / P.S. Goldman-Rakic // Neuron. — 1995. — Vol. 14, № 3. — P. 477–485.
- Chafee M. V. Matching Patterns of Activity in Primate Prefrontal Area 8a and Parietal Area 7ip Neurons During a Spatial Working MemoryTask / M. V. Chafee, P.S. Goldman-Rakic // Journal of Neurophysiology. — 1998. — Vol. 79, № 6. — P. 2919–2940.
- Hampson R.E. Categorization in the monkey hippocampus: A possible mechanism for encoding information into memory / R.E. Hampson, T.P. Pons, T.R. Stanford, S.A. Deadwyler // Proceedings of the National Academy of Sciences. — National Academy of Sciences 2004. — Vol. 101, № 9. — P. 3184–3189.
- Miller E.K. Neural Mechanisms of Visual Working Memory in Prefrontal Cortex of the Macaque / E.K. Miller, C.A. Erickson, R. Desimone // Journal of Neuroscience. — Society for Neuroscience 1996. — Vol. 16, № 16. — P. 5154–5167.
- Amit D. Model of global spontaneous activity and local structured activity during delay periods in the cerebral cortex / D. Amit, N. Brunel // Cerebral Cortex. — 1997. — Vol. 7, № 3. — P. 237–252.
- Kornblith S. Stimulus Load and Oscillatory Activity in Higher Cortex / S. Kornblith, T.J. Buschman, E.K. Miller // Cerebral Cortex. — Oxford University Press2016. — Vol. 26, № 9. — P. 3772–3784.
- Lundqvist M. Gamma and Beta Bursts Underlie Working Memory / M. Lundqvist, J. Rose, P. Herman, S.L. Brincat, T.J. Buschman, E.K. Miller // Neuron. — Cell Press 2016. — Vol. 90, № 1. — P. 152–164.
- Siegel M. Phase-dependent neuronal coding of objects in short-term memory. / M. Siegel, M.R. Warden, E.K. Miller // Proceedings of the National Academy of Sciences of the United States of America. — National Academy of Sciences 2009. — Vol. 106, № 50. — P. 21341–21346.
- Engel A.K. Beta-band oscillations — signalling the status quo? / A.K. Engel, P. Fries // Current Opinion in Neurobiology. — Elsevier Current Trends 2010. — Vol. 20, № 2. — P. 156–165.
- Kopell N. Neuronal assembly dynamics in the beta1 frequency range permits short-term memory. / N. Kopell, M. A. Whittington, M. A. Kramer // Proceedings of the National Academy of Sciences of the United States of America. — National Academy of Sciences 2011. — Vol. 108, № 9. — P. 3779-3784.
- Lundqvist M. Theta and gamma power increases and alpha/beta power decreases with memory load in an attractor network model. / M. Lundqvist, P. Herman, A. Lansner // Journal of Cognitive neuroscience — 2011 — Vol. 23, № — P. 3008-3020
- Dipoppa M. Flexible frequency control of cortical oscillations enables computations required for working memory. / M. Dipoppa, B.S. Gutkin // Proceedings of the National Academy of Sciences of the United States of America. — National Academy of Sciences 2013. — Vol. 110, № 31. — P. 12828-12833.
- Schmidt H. Network mechanisms underlying the role of oscillations in cognitive tasks. / H. Schmidt, D. Avitabile, E. Montbrio, A. Roxin // PLoS computational biology — 2018 — Vol. 14, № 9.
- Voronenko S.O. Weakly nonlinear response of noisy neurons / S.O. Voronenko, B. Lindner // New Journal of Physics. — IOP Publishing 2017. — Vol. 19, № 3. — P. 033038.