Опубликовать статью Вход и регистрация
Расширенный поиск
Разделы статьи

ТОЧЕЧНО-ЭПЮРНЫЕ ДВУХОКТАНТОВЫЕ НОМОГРАММЫ

Научная статья
Левкин Ю.С.
DOI:
https://doi.org/10.23670/IRJ.2018.67.100
Выпуск: № 1 (67), 2018
Опубликована:
2017/12/29
PDF

Левкин Ю.С.

Соискатель,

Тольяттинский государственный университет ТГУ

ТОЧЕЧНО-ЭПЮРНЫЕ ДВУХОКТАНТОВЫЕ НОМОГРАММЫ

Аннотация

В статье предлагается новое направление использования эпюрных номограмм в качестве технологий обработки экспериментальных данных. На базе начертательной геометрии при использовании её терминологии, строятся в октантовых ячейках аксонометрии. Эти аксонометрические проекции характеризуют не цифровую абстракцию, а   параметровую проекционную связь экспериментальных физических величин. В работе с эпюрными номограммами требуются новые понятия и характеристики параметров, определяющих аргументальные и функциональные значения геометрических образов. Статья не рассматривает вопрос усовершенствования известного материала, она рассматривает необходимость применения графической технологии, решающей научно - экспериментальные задачи, поскольку игнорирование их не даст полноты понимания физических процессов. Точечно – эпюрные номограммы с помощью многомерности своих параметров способны оценить геометрические образы (прямые линии, кривые линии, плоскости, поверхности), получив такие изображения, которые позволят, технически грамотному специалисту увидеть то, что видит студент, глядя на аксонометрию детали. Приведённые номограммы наглядно представляют графику, которую можно использовать при обосновании экспериментальных выводов. Все построения основаны на закономерностях, применяемых в начертательной геометрии. Начертательная геометрия служит ключевой общетехнической дисциплиной, которая с математической точностью осуществляет графические и основанные на её методике номографические построения. В статье предлагаются авторские теоремы и иллюстрации номограмм.

Ключевые слова: начертательная геометрия, функциональные и аргументирующие оси, линии связи, аксонометрические проекции, двух октантовая номограмма.

Levkin Yu.S.

Postgraduate student. Togliatti State University

POINT-EPURE TWO-OCTANE NOMOGRAPHS

Abstract

The paper proposes a new direction for the use of epure nomograms as technologies for processing experimental data. The axonometry is constructed in octant cells based on the descriptive geometry, when using its terminology. These axonometric projections characterize not the digital abstraction, but the parametric projection relationship of the experimental physical quantities. New concepts and characteristics of parameters determining the argument and functional values of geometric patterns are required in the work with epure nomograms. The paper does not consider the improvement of a well-known material; it considers the need for the use of graphic technology to solve scientific and experimental problems, since their ignoring will not provide a full understanding of physical processes. The point-epure nomograms with the help of the multidimensionality of their parameters are able to evaluate geometric images (straight lines, curved lines, planes, surfaces), having obtained such images that will enable a technically competent specialist to see what the student sees looking at the axonometry of the detail. The given nomograms graphically represent the schedule, which can be used to justify the experimental conclusions. All constructions are based on the regularities used in descriptive geometry. Descriptive geometry serves as a key general technical discipline that implements graphically and graphically based on its methodology nomographic constructs. The author proposes author's theorems and illustrations of nomograms.

Keywords: descriptive geometry, functional and argumentating axes, communication lines, axonometric projections, two octant nomograms.

Номография происходит от слова names – закон и является разделом математики, объединяющий теорию и практические методы построения номограмм – специальных чертежей, являющихся изображениями функциональных и аргументальных зависимостей  [16, С.4].

Геометрия — это составная часть математики, а начертательная геометрия одна из её видов. Отличительной чертой генезиса геометрических построений от номографических, является превращение геометрических осей в физические параметральные величины. В зависимости от числа абстрактных осей (X, Y, Z) с их иррациональными продолжениями (-X, -Y, -Z), строятся параметрические модели, где эти оси трансформируются в конкретные физические величины (X - Qг ),  (Y - Qв),  (Z - ωг) и т.д.  Других ограничений при построении номограмм нет, что даёт возможность использовать все закономерности начертательной геометрии при построении номограмм [5, С.37 – 47.], [6, С. 80], [12,  С. 420], [14, С, 224]

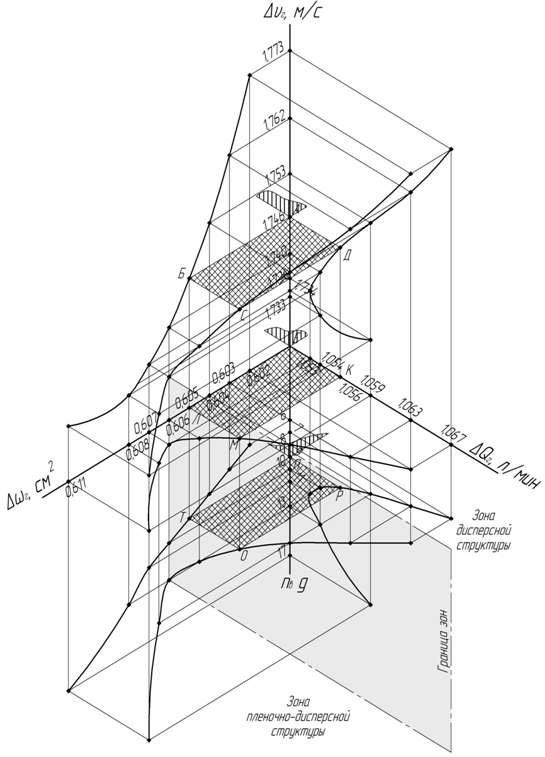
Оси точечно–эпюрных номограмм. Многомерные номограммы строятся в октантовых ячейках. Количество выбранных осей эпюрной номограммы зависит от количества размещённых на них экспериментальных параметров. В связи с этим эпюрные номограммы могут быть октантовыми, двухоктантовыми, трёхоктантовыми и т.д., в зависимости от количества параметров, участвующих в эксперименте. Каждая ячейка номограммы должна строиться с учётом смежной зависимости параметров, а функциональная ось занять положительное или отрицательное направление аппликаты. На рис.1. функционольная ось ∆ υ м/с, а иррациональное ей продолжение nв(g) будет занимать промежуточную функциональность т.к. она, находясь в нижнем ярусе и собирает проекционную информацию параметров этого яруса. Аргументирующие параметры, нижнего яруса (∆Qг, ∆ωг nв)  при помощи линий связи замыкают проекционную связь на функциональном параметре, показывая зависимость аргумеотальных значений от функциональных.  Используем аналитический пример. Формулой 27-02-2018 17-28-27 можно описать зависимость  функции (∆ υг) рис.1. от переменных (∆Qг,  и  ∆ωг)  аргументальных  параметров. Экспериментальный точечный замер параметров, связанных между собой линиями связи на рис. 1, показывает, что аргументальные параметры формулы будут равны функциональным значениям. Такая зависимость наблюдается и на графической иллюстрации.

  1. Аргументальные оси эпюрной номограммы, это такие оси, которые являются носителями физических переменных, тех или иных параметров.
  2. Функциональная ось эпюрной номограммы - это ось аппликат, которая является носителем результирующего параметра.

Иррациональное аппликатное направление оси nв(g), нельзя считать функциональным, т.к. параметр этой оси имеет аргументальную характеристику. Однако такую ось нельзя считать чисто аргументальной т.к., объединяя две оси четвёртой октанты, она способствует построению аксонометрии. Собирательную аргуменальность оси nв(g) можно, считать, промежуточной функциональностью т.к.:

  1. Аргументальные оси четвёртой октанты (∆Qг, и ∆ωг)  позиционируют ось nв(g) как функциональную.
  2. Все проекции точек нижнего яруса имеют проекционную связь с осью nв(g).
  3. Благодаря оси nв(g) построена аксонометрия, объединяющая пространственную совокупность трёх осей рис. 1. (nв, Δωг, ΔQг).
  4. Варьирование проекционных точек на оси nв(g), является показателем изменения функциональных значений оси ∆ υг при помощи линий связи.

Плоскости точечно – эпюрных номограмм. Горизонтальная плоскость разделяет номограмму на два яруса. Эта плоскость делит также фронтальную и  профильную плоскости, являясь определителем октантовых ячеек верхнего (І, ІІ, V, VІ), и октантовых ячеек нижнего яруса (ІІІ, ІV, VІІ, VІІІ) [1, С.15], [2, С.44 – 54], [13, С.262], [15, С.224].

Фронтальную и профильную плоскости на рис.1. в верхнем ярусе можно считать функциональными плоскостями, т.к. их пересекают  горизонтальные плоскости уровня, которые также пересекают графические зависимости точечных  экспериментальных замеров, и лежат выше горизонтальной плоскости. Так верхняя плоскость уровня пересекает двухмерные зависимости в точках Б и Д,  и аксонометрию в точке С. Все эти значения аргументальных точек связаны линиями связи с  функциональной точкой А и лежат на одной горизонтальной плоскости уровня А, Б, С и Д.

Все плоскости уровня, лежащие выше горизонтальной плоскости,  являются функциональными, если функциональной осью принята ось, лежащая выше горизонтальной плоскости.

Фронтальная и  профильная плоскости в нижнем ярусе являются аргументальными плоскостями, т.к. их пересекают горизонтальные плоскости уровня, которые также пересекают графические зависимости точечных  экспериментальных замеров, и лежат ниже горизонтальной плоскости.  Нижняя плоскость уровня пересекает двухмерные зависимости в точках Т и Р,  и аксонометрию в точке О. Все эти значения аргументальных точек связаны линиями связи с промежуточной функциональной точкой Л и лежат на одной горизонтальной плоскости уровня Т, О, Р и Л. Проекции точек Т, Р и О, имеют проекционную связь с точками Б, Д, С, с лежащими на верхней горизонтальной плоскости уровня,  которая пересекает функциональную ось Δυ г.

Таким образом, любая точка на функциональной оси является результирующим точечным параметром всех участвующих в эксперименте физических величин, связанных с ней линиями связи.

Аргументальная плоскость, это такая плоскость, которая является носителем переменных аргументальных зависимостей, такой плоскостью, при использовании эпюрной октантовой номографической модели, является октантовая горизонтальная плоскость.

Точечный замер – это один из моментальных экспериментальных замеров всех параметров, соединённых замкнутой целью линий связи.

Любой, произвольно взятый, точечный замер на рис. 1. может быть определён двумя горизонтальными плоскостями уровня (А, Б, С и Д верхний ярус ), (Т, О, Р и Л нижний ярус ) и горизонтальной плоскостью (Е, Л, М и К). Одна плоскость  пересекает функциональную ось ∆ υг верхнего яруса,  другая является промежуточно-функциональной и пересекает нижний ярус с осью nв(g), а третья рабочая горизонтальная разделяет октанты на два яруса.

Описание номограммы рис. 1.  Количественные зависимости параметров ∆Q, ∆ω и ∆υ и nв = 9 ÷ 23g, при частоте fв = 150 Гц. Точечно-эпюрная двухоктантовая номограмма определяет смену структурного режима двухфазного потока. На рис. 1. она показана затенённой горизонтально проецирующей плоскостью. Место раздела проходит по критическим проекционным точкам. Каждая часть разделённой кривой имеет свою эмпирическую закономерность. Эксперимент проводился с дисперсной структурой. Под действием варьирования вибрационного ускорения nв = 9 ÷ 23g, при частоте fв = 150 Гц. Исходная структура трансформировалась в дисперсионно – плёночную, что подтверждает фото материал и самое главное эпюрная номограмма [9, С.96]. Вот почему конфигурация кривых до критических точек соответствует одной структуре, а после её раздела изменяет первоначальное положение. Таким образом, эпюрная двух октантовая номограмма способствует не только нахождению функционального значения любого точечного замера, при помощи проекционной связи, но и нахождению смены физических закономерностей и их обоснование при помощи графических построений. Для того чтобы образно показать работу эпюрной номограммы достаточно сравнить её с проводником электрического тока. Любую парметровую проекцию точки сравним с электрической лампой, линии связи, с проводником электрического тока, функциональную проекцию точки с электрической лампой иного цвета. И так, зная лишь один точечный замер одного из параметров, при помощи линий связи получим не только функциональный результат, но и параметровую арументальную связь, каждого точечного замера проведённого эксперимента. На рис. 1. штриховкой отмечены две горизонтальные плоскости уровня (А, Б, С и Д верхний ярус ), (Т, О, Р и Л нижний ярус ) и горизонтальной плоскостью (Е, Л, М и К ). Линии связи, соединяющие эти точки, являются линиями связи одного точечного замера.

Точки пересечения плоскостей уровня с геометрическими образами, определяют точечные  экспериментальные замеры [7, С.69 - 74].

Любая горизонтальная плоскость уровня,  пересекающая функциональную ось Δυг в любой её точке, пересекает геометрические образы номографических параметров верхнего октантного яруса. Эти пересечения, являются  функциональными, определителями любых замеров, рассматриваемого яруса [9, С. 69 - 76].

27-02-2018 17-29-41

Рис. 1 – Точечно – эпюрная  двухоктантовая номограмма [9, С.96].

(Количественные зависимости параметров ∆Q, ∆ω и ∆υ и nв = 9 ÷ 23g, при частоте fв = 150 Гц.)

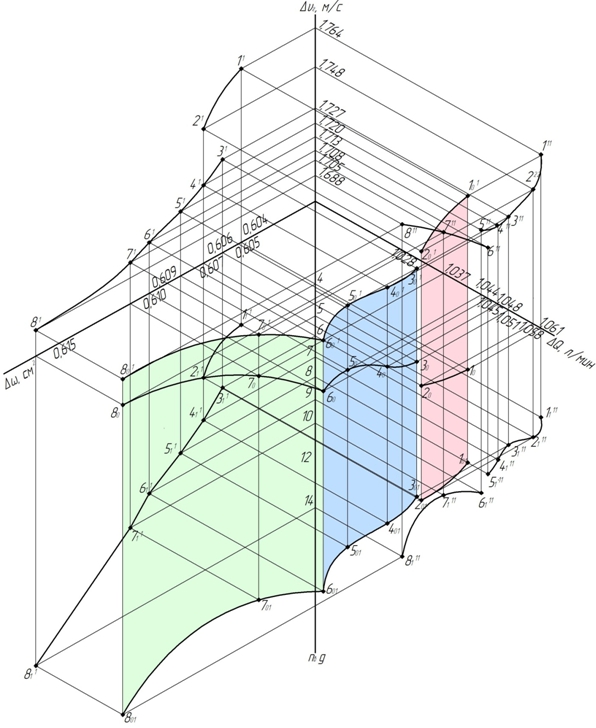
Описание номограммы рис.2.  Влияния вибрационных ускорений nв = 4 ÷ 14(g) при fв = 100 (Гц)  на скорость двухфазного дисперсного потока с последующей его трансформацией. На рис. 2., как и на рис. 1., все связанные между собой линиями связи проекции точек, указанных ниже, являются точками одного замера и  определителями одной из функциональных материальных точек [3, С.37 – 47, 4, С.112].

 Проекции траекторией точек кривой, лежащие на горизонтальной плоскости 80, 70, 60, 50, 40, 30  являются ей экспериментальными замерами и принадлежат также горизонтально - проецирующейся поверхности. Проекции траекторией точек кривой 801, 701, 601, 501, 401, 301,,, лежат на горизонтально - проецирующейся поверхности и пересекаются её нижней горизонтальной плоскостью уровня, которая находится ниже горизонтальной плоскости.  Поверхность раскрашена  тремя цветами. Каждый из цветов горизонтально - проецирующейся поверхности соответствует своей структуре газожидкостного потока. Салатный цвет соответствует дисперсной структуре, синий цвет - дисперсионно – плёночной, а розовый неустановившемуся потоку.

Проекции траекторией точек кривой 810, 710, 610, 510, 410, 310, лежит на горизонтально - проецирующейся поверхности, и пересекаются с верхней горизонтальной плоскостью уровня, которая находится выше горизонтальной плоскости.  Эта секущая горизонтальная плоскость уровня проходит через фронтальную и профильную плоскость. Пересечение этой  плоскостью ось ∆υ,  является функциональным определителем графических закономерностей.

Получение любой поверхности эпюрной номограммы определяет связь проекций точек нижнего и верхнего ярусов линиями связи, проходящих параллельно направлению  осей ∆υ, nв. Линии связи, проходящие через точки  801, 80, 810; 701, 70, 710; 601, 60, 610; 501, 50, 510; 401, 40, 410; 301, 30, 310; 201, 20, 210; 101, 10, 110, выполняют функции образующей поверхности эпюрной номограммы. Отсюда следует.

І. Теорема: если две точки, принадлежащие двум аксонометрическим проекциям, связанны между собой перпендикулярными линиями связи, то такие отрезки являются образующими эпюрной номографической двухоктантовой поверхности.

Аксонометрические проекции кривых верхнего и нижнего ярусов, являются направляющими номографической поверхности, а образующие этой поверхности пересекают горизонтальную плоскость по горизонтальным проекциям третьей направляющей. Отсюда следует:

ІІ. Теорема: Если две аксонометрические проекции, параметральных геометрических образов, представленны траекториями точек, которые пересекаются образующими номографической поверхности, и эти образующие пересекают горизонтальную плоскость по траекториям точек горизонтальной проекции экспериментальной аргументальной зависимости, то эти три проекции являются направляющими двухоктантовой эпюрной номограммы.

Плоскости, которые образуют октантовые ячейки, при помощи линий связи двухмерных графиков,  могут охарактеризовать общую картину эксперимента. Однако аксонометрический аналог материализует, номографической иллюстрацией, органическую связь параметров всего эксперимента. Чтение  рис. 2. позволяет понять природу эксперимента, её физические характеристики, а также изменения функциональной зависимости, от варьирования аргументальных параметров.

Выводы.

Графические зависимости, выражаются  геометрическим элементом (прямая, кривая и т.д.), а точечно -  эпюрная номограмма позволяет контролировать экспериментальный процесс.

27-02-2018 17-30-37

Рис. 2 – Двухоктантовая номограмма. Влияния вибрационных ускорений nв = 4 ÷ 14(g) при fв = 100 (Гц) на скорость двухфазного дисперсного потока с последующей его трансформацией [11, С 47 ].

Если в процессе эксперимента появляется резкое отклонение от первоначальной закономерности, которая выражается уходом одной из точек от траектории графического элемента (прямая становится ломанной прямой),  то замер ошибочный.

Ошибочные точечные замеры могут иметь субъективные и объективные характеристики, уменьшающие точность замера.

Точечно-эпюрная двухоктантовая номограмма позволяет определять на графических участках номограммы аномальные участки, физическое объяснение, которых возможно при тщательном анализе геометрических образов [8, С.112 - 119]. Не следует путать графические аномальные участки с одной или несколькими ошибочными точками, определяющими геометрические образы. Примером аномального участка может служить участок точек 1-2 рис. 2.

Аномальный графический участок, это автономный участок, лежащий между двумя графическими закономерностями или рядом с одним из них на рис. 2. он окрашен в розовый цвет.

На рис. 2. на проекциях двухмерных зависимостей такие участки показаны разрывом с последующим изменением направлением траекторий кривых. Аксонометрические, оторванные от основных кривых, участки номограммы демонстрируют геометрическое отличие от первоначальных закономерностей, разрывом траектории.

Точечно-эпюрная двухоктантовая номограмма позволяет определить изменения первоначальных характеристик эксперимента. В процессе проведения опыта, под влиянием параметральных показателей, жидкость может превратиться в двухфазную смесь, изменить   первоначальную структуру потока и т.д.

На рис. 2. эпюрная двухоктантовая номограмма демонстрирует переход, дисперсной структуры, в дисперсно-плёночную структуру. Смена структур показана разделительной, затенённой плоскостью рис.1. На фотографиях даётся дополнительный контроль этого перехода, но даже фотографии не дают чёткую информацию, предлагаемую номограммой. Базируясь на вышеизложенных выводах можно сделать заключение.

ІІІ. Теорема: если траектории точек кривых подчиняются закономерности увеличения или уменьшения одного параметра относительно другого, то нарушение такой закономерности изменяет первоначальное направление геометрического образа, что приводит к изменению физического состояния одного или нескольких экспериментальных параметров.

Список литературы / References

  1. Гордон В.О., Семенцов – Огиевский М.А. Курс начертательной геометрии/ В.О. Гордон, М.А. Семенцов – Огиевский, М.,1988,2002. С. 272.
  2. Сальков Н.А., Начертательная геометрия – база для геометрии аналитической / Н.А. Сальков. // Геометрия и графика. – 2016. - Т. 4. - №1. - С.44 – 54. -  DOI; 10.12737/18057.
  3. Сальков Н.А., Начертательная геометрия – база для компьютерной графики / Н.А. Сальков. // Геометрия и графика. – 2016. - Т. 4. - №2. - С.37 – 47. - DOI; 10.12737/19832.
  4. Сальков Н.А., Начертательная геометрия – теория изображений / Н.А. Сальков // М.: ИНФРА - М., - 2013. - С. 174.
  5. Сальков Н.А., Начертательная геометрия – базовый курс / Н.А. Сальков // Геометрия и графика. – 2016. - Т.4.- №2. - С.37 – 47. - DOI; 10.12737/19832.
  6. Климухин А.Г. Начертательная геометрия. // А.Г Климухин. М.. - 1973. - С. 368.
  7. Левкин Ю.С. Получение четырёхмерных номограмм на базе теоремы подобия. // Ю.С. Левкин Геометрия и графика – М. – 2017. – С. 69 – 74. DOI; 10.12737/article_5953f789301109.
  8. Левкин Ю.С. Влияние вибрационных колебаний на характеристики структуры двухфазного потока. // Ю.С. Левкин. Изв. Вузов. Сев.-Кавк. регион. Технические науки. - Новочеркасск – 2016 - № 2. – С. 112 - 119.
  9. Левкин Ю.С. Некоторые структуры газожидкостных потоков в поле вибрации. / Ю.С. Левкин - Монография. Самарский государственный авиационный университет -  тираж 200 экз. -  Самара 2016. - С. 113.
  10. Левкин Ю.С. Построение эпюрной номограммы на базе теоремы совмещения // Ю.С. Левкин Международный научно-исследовательский журнал Екатеринбург, №10 – (64) – ч.3 - Октябрь- 2017 – С 69 - 76. – D01- htths/10/23670/IRJ/2017/64/079.
  11. Левкин Ю.С. Влияние вибрационных колебаний fв 30 ÷ 100(гц) на параметры гидродинамических характеристик. // Ю.С. Левкин Изв. Вузов. Сев.- Кавк. регион. Технические науки. - № 4. - Новочеркасск. – 2017. – С. 47.
  12. Начертательная геометрия /Н.Ф.Четверухин, В.С. Левицкий З.И. Прянникова и др. М., Высшая школа. - 1963. - С. 420.
  13. Начертательная геометрия / С.М. Колотов, М.Ф. Вестефеев, В.Е. Мехайленко, и др. Киев: Вища школа. - 1975. - С. 262.
  14. Начертательная геометрия / Н.Н. Крылов, Г.С. Иконникова, В.Л. Николаев, В.Е.Васильев. М. Высшая школа. - - С. 224.
  15. Иванов Г.С. Начертательная геометрия./ Г.С. Иванов/ М. Машиностроение - 1995. - 224с.
  16. Зуева Н.М. Номограммы.// Н.М. Зуева МБОУ– 2013. – С.15 .

Список литературы на английском языке / References in English

  1. Gordon V.O., Sementsov — Ogievsky M.A. Kurs nachertatel'noy geometrii [Course Descriptive Geometry] / [Text] / V.O. Gordon, M.A. Sementsov — Ogievsky, Moscow, 1988,2002. P. 272. [In Russian]
  2. Salkov N.A. Nachertatel'naya geometriya – baza dlya geometrii analiticheskoy [Descriptive Geometry - Basis for Analytical Geometry] [Text] / N.A. Salkov // Geometry and graphics. - 2016. - V. 4. - No. 1. - P.44 - 54. - DOI; 10.12737 / 18057. [In Russian]
  3. Salkov N.A. Nachertatel'naya geometriya – baza dlya komp'yuternoy grafiki  [Descriptive Geometry - Base for Computer Graphics] [Text] / N.A. Salkov // Geometry and graphics. - 2016. - V. 4. - No. 2. - P.37 - 47. - DOI; 10.12737 / 19832. [In Russian]
  4. Salkov N.A. Nachertatel'naya geometriya – teoriya izobrazheniy [Descriptive Geometry - Image Theory] [Text] / N.A. Salkov // Moscow: INFRA - M., - 2013. - P. 174.
  5. Salkov N.A. Nachertatel'naya geometriya – bazovyy kurs [Descriptive Geometry - Basic Course] [Text] / N.A. Salkov // Geometry and graphics. - 2016. - V.4.- No.2. - P.37 - 47. - DOI; 10.12737 / 19832. [In Russian]
  6. Klimukhin A.G. Nachertatel'naya geometriya [Descriptive Geometry]. [Text] // A.G. Klimukhin. M. - 1973. - P. 368. [In Russian]
  7. Levkin Yu.S. Polucheniye chetyrokhmernykh nomogramm na baze teoremy podobiya [Obtaining Four-dimensional Nomograms on Basis of Similarity Theorem] / [Text] // Yu.S. Levkin. Geometry and graphics - M. - 2017. - P. 69 - 74. DOI; 10.12737 / article_5953f33427942.789301109. [In Russian]
  8. Levkin Yu.S. Vliyaniye vibratsionnykh kolebaniy na kharakteristiki struktury dvukhfaznogo potoka [Influence of Vibration Oscillations on Characteristics of Structure of a Two-phase Flow] // [Text] // Yu.S. Levkin. Bul. of high schools. North-Caucasus. region. Technical science. - Novocherkassk - 2016 — No. 2. - P. 112 — 119. [In Russian]
  9. Levkin Yu.S. Nekotoryye struktury gazozhidkostnykh potokov v pole vibratsii [Some Structures of Gas-liquid Flows in Field of Vibration] // [Text] / Yu.S. Levkin - Monograph. Samara State Aviation University - 200 copies. - Samara 2016. - P. 113. [In Russian]
  10. Levkin Yu.S. Postroyeniye epyurnoy nomogrammy na baze teoremy sovmeshcheniya [Construction of Eccentric Nomogram Based on Theorem of Coincidence] / [Text] // Yu.S. Levkin International Scientific and Research Journal, Ekaterinburg, No. 10 - (64) - Part 3 - October - 2017 - From 69 - 76. - D01-htths / 10/23670 / IRJ / 2017/64/079. [In Russian]
  11. Levkin Yu.S. Vliyaniye vibratsionnykh kolebaniy fv 30 ÷ 100(gts) na parametry gidrodinamicheskikh kharakteristik [Influence of Vibrations fв 30 ÷ 100 (Hz) on Parameters of Hydrodynamic Characteristics] [Text] // Yu.S. Levkin Bul. of High schools. North-Caucasus. region. Technical science. - No. 4. - Novocherkassk. - 2017. - P. 47. [In Russian]
  12. Nachertatel'naya geometriya [Descriptive Geometry] / [Text] / N.F. Chetverukhin, V.S. Levitsky Z.I. Pryannikova et al. M., High School. - 1963. - P. 420. [In Russian]
  13. Nachertatel'naya geometriya [Descriptive Geometry] // [Text] / S.M. Kolotov, M.F. Vestefeev, V.E. Mehaylenko, et al. Kiev: Vishcha school. - 1975. - P. 262. [In Russian]
  14. Nachertatel'naya geometriya [Descriptive Geometry] // [Text] / N.N. Krylov, G.S. Ikonnikova, V.L. Nikolaev, V.E. Vasiliev. M. High school. - 2000. - P. 224. [In Russian]
  15. Ivanov G.S. Nachertatel'naya geometriya [Descriptive Geometry] / G.S. Ivanov / [Text] / M. Mechanical Engineering - 1995. - 224 p. [In Russian]
  16. Zueva N.M. Nomogrammy [Nomograms] / [Text] / N.M. Zueva MBOU-2013. - P.15. [In Russian]