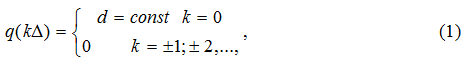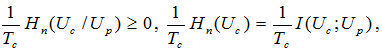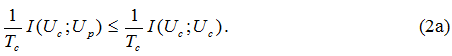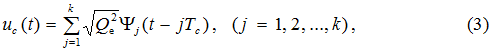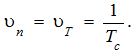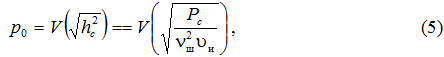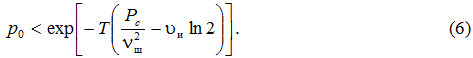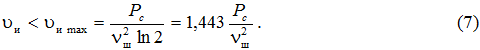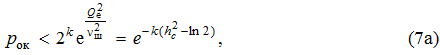ТАЙМЕРНЫЕ СИГНАЛЫ КАК ИНСТРУМЕНТАРИЙ ФОРМИРОВАНИЯ УКРУПНЕННЫХ СИГНАЛЬНЫХ КОНСТРУКЦИЙ
Захарченко Н.В.1, Бектурсунов Д.Н.2, Гранатурова И.Б.3, Полищук С.А.4
1Доктор технических наук, 2Аспирант, 3Аспирант, 4Аспирант, Одесская национальная академия связи
ТАЙМЕРНЫЕ СИГНАЛЫ КАК ИНСТРУМЕНТАРИЙ ФОРМИРОВАНИЯ УКРУПНЕННЫХ СИГНАЛЬНЫХ КОНСТРУКЦИЙ
Аннотация
Введены численные параметры степени укрупнения отдельных сигналов и сигнальных конструкций, проведен анализ влияния параметров таймерных сигналов (i, m, s) на степень укрупнения.
Ключевые слова: таймерные сигналы, укрупненные сигналы, сигнальные конструкции.
Zakharchenko N.V.1, Bektursunov D.N.2, Granaturova I.B.3, Polishchuk S.A.4
1Ph.D., 2Graduate, 3Graduate, 4 Graduate, Odessa National Academy of Telecommunications
TIMING SIGNALS AS A TOOLS OF FORMATION ENLARGEMENT SIGNAL STRUCTURES
Abstract
Introduced numerical parameters of the degree of integration of the individual signals and signal structures, the analysis of influence of parameters of timing signals (i, m, s) the degree of integration.
Keywords: timing signals, enlarged signals, signal design.
Укрупненными сигналами называют сигналы, удовлетворяющие условию селективности (первому критерию Найквиста – отсутствию межсимвольных искажений МСИ), что накладывает следующие ограничения на импульсную реакцию [1]:
где d – некоторая заданная величина, определяемая сигналом [1]
t0 – произвольный начальный момент отсчета; Δt – шаг дискретизации в моменты (kΔt + t0).
При передаче сигнала в канал информация изменяет один (или несколько) параметров (длительность, амплитуду, фазу, частоту или комбинации этих параметров).
При заданном алфавите источника и любом преобразовании сигналов, происходящем в канале связи, скорость передачи информации не может возрастать. Действительно, при преобразовании исходных сигналов {Uc} в выходной алфавит канала {Up} величина скорости υи определяется
При известной энтропии Нп и соотношении преобразования входного сигнала Uс в выходной алфавит Uр
скорость передачи информации υи определяется как [1]
Знак равенства в выражении (2а) имеет место только тогда, когда H (Uc / Up), то есть если по принятому сигналу можно полностью восстановить передаваемый [2]. Это значит, что операция преобразования обратима. Необратимые преобразования всегда сопровождаются потерей некоторой доли информации об исходном сигнале. В этом случае выражение (2а) становится строгим неравенством, что позволяет рассматривать H (Uc / Up) как средние потери информации в канале. Здесь имеется определенная аналогия со вторым законом термодинамики, согласно которому энтропия обратимых процессов не меняется, а при необратимых процессах возрастает.
Потери информации о сигнале далеко не всегда сопровождаются уменьшением полезной информации. Так, например, сужение полосы пропускания в военных системах телефонии до 2400 Гц ухудшает художественное восприятие языка, но практически не снижает разборчивости речи. Это означает, что во многих случаях сообщения и сигналы имеют естественную избыточность, устранение которой не только не влияет на верность связи, но в ряде случаев полезно для повышения ее скорости υи. Так, в частности, происходит при статически оптимальном кодировании. Наряду с этим в сигналы часто искусственно вводят избыточность для повышения помехоустойчивости. Примером этого являются помехоустойчивые коды.
Известно, что для повышения верности связи при наличии помех часто применяются специальные помехоустойчивые коды. С этой целью в k-значные кодовые комбинации можно ввести по определенному алгоритму i дополнительных проверочных символов, которые не отражают непосредственно сообщения и служат для обнаружения и исправления ошибок. При этом результирующая значимость кода станет n = k + l. Введение проверочных символов создает избыточность кода, поскольку с помощью n-значных комбинаций потенциально можно передать M0 = 2n = 2lM сообщений.
Если число сообщений М и время Т заданы, то использование избыточных кодов требует увеличения числа передаваемых символов в единицу времени. Это, в свою очередь, сопряжено с уменьшением их длительности при условии, что полоса ΔF>1/t0, следовательно, уменьшением удельной энергии Qc2. В результате величина hc2 уменьшается, что приводит к повышению вероятности ошибки приема символов.
Таким образом, оба фактора – увеличение избыточности кода и уменьшение удельной энергии кодовых символов, при фиксированном времени передачи, влияют на верность связи. Сюда относятся, например, системы передачи информации с космических аппаратов, где энергетические ресурсы бортовых источников питания ограничены.
Для иллюстрации влияния параметра Qc2 на верность связи рассмотрим два способа передачи сообщений. При первом способе, условно называемом по символьным, сигналы представляют собой k-значные двоичные кодовые комбинации с энергией kQe2=υiTkQe2 Дж и передаются по каналу связи символ за символом. При втором способе, называемому передачей укрупненными сигналами, алфавит сигналов образован множеством 2k ортогональных импульсов с удельной энергией Qy2=kQe2; передача j-го символа, соответствует j-му сообщению (двоичном числу), производится в момент окончания формирования этого сообщения источником.
Определим вероятность ошибки для обоих способов передачи.
Посимвольная передача. Пусть, например, необходимо передать сообщение 1011. Выберем для этой цели ортогональные сигналы, описываемые выражением [2]
где Ψj(t) – нормированная по энергии координатная функция, представляющая собой импульс длительностью Тс с единичной энергией; k=υиTk – число двоичных символов в кодограмме продолжительностью Tk. В этом случае величина скорости
Таким образом, передача одного сообщения занимает Tk секунд. Разместим все М = 2k сигналов в вершинах 2k-мерного гиперкуба. Тогда вероятность хотя бы одиночной ошибки будет
где вероятность искажения двоичного символа р0 определяется выражением
где V(·) – интеграл вероятности.
Если прием сигналов осуществляется посимвольно, то решения по каждому символу принимаются независимо друг от друга с использованием, например, критерия максимума правдоподобия [2].
Как следует из (4) при заданных Pc и υи вероятность ошибки возрастает с увеличением продолжительности кодограммы; при фиксированном Tk вероятность p0и может быть сделана малой только путем увеличения удельной энергии элементарного символа Qe2=Qc2 (средней мощности сигнала Pc или снижением скорости передачи информации υи).
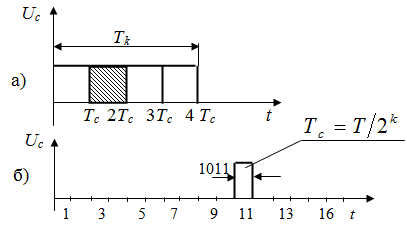
Передача укрупненными сигналами. Пусть по-прежнему сообщения передаются один раз за T = Tk секунд. Это означает, что в течение времени Tk передается один из 2k ортогональных импульсов. Так, на рис. 1а изображен случай передачи сообщения 1011.
Передаваемый сигнал
где Ψj (t - jTc) – нормированная по энергии координатная функция, представляющая собой импульс с единичной энергией длительностью ![]() ; j = 0, 1, …, 2k – 1.
; j = 0, 1, …, 2k – 1.
Рис. 1 - О влиянии скорости передачи информации на вероятность связи
Так как величина функции ![]() , то вероятность ошибки для М равновероятных ортогональных сигналов с одинаковой энергией ограничена значением
, то вероятность ошибки для М равновероятных ортогональных сигналов с одинаковой энергией ограничена значением ![]() . Подставив сюда значения
. Подставив сюда значения ![]() , получим
, получим
Из формулы (6) следует, что при передаче укрупненными ортогональными сигналами вероятность ошибки экспоненциально убывает с увеличением Т до тех пор, пока скорость передачи информации удовлетворяет условию
Переписав выражение (6) в виде
получим эквивалентную форму выражения (7):
Выражение (8) имеет простую физическую интерпретацию.
Так как vш2=k0T0 дж/град, где постоянная Больцмана k0 = 1,38 10-23 дж/град, то для передачи 1 дв.од. информации по каналу связи с нормальным белым шумом (гауссов канал) сигнал должен обладать удельной энергией 0,693k0Т0 дж.
Сравнение выражений (4) и (7а) показывает, что при посимвольной передаче вероятность р0 → 1 с увеличением k независимо от значения (при передаче укрупненным сигналами hc2>0,693 вероятность р0 → 0 с возрастанием k). Следовательно, параметр hc2 определяет верхнюю границу скорости передачи информации υи max. При υи < υи max вероятность рок может быть сделана сколь угодно малой с увеличением Т.
Такое различие в характере изменения величины рок объясняется следующим. При посимвольной передаче сигналы размещаются в вершинах k-мерного гиперкуба и расстояние между ближайшими сигналами ![]() сохраняется постоянным при увеличении k, в то время как мерность пространства сигналов и число «ближайших» точек в этом пространстве растут линейно. Поэтому вероятность попадания результирующего вектора Up=Uc+Uш в соседнюю зону решения с увеличением k возрастает. При передаче укрупненным ортогональными сигналами расстояние между ближайшими точками k-мерного пространства равно
сохраняется постоянным при увеличении k, в то время как мерность пространства сигналов и число «ближайших» точек в этом пространстве растут линейно. Поэтому вероятность попадания результирующего вектора Up=Uc+Uш в соседнюю зону решения с увеличением k возрастает. При передаче укрупненным ортогональными сигналами расстояние между ближайшими точками k-мерного пространства равно ![]() , то есть возрастает пропорционально
, то есть возрастает пропорционально ![]() . При увеличении мерности пространства от kj-1 до kj прирост расстоянии достигается путем добавления мерности для каждого из
. При увеличении мерности пространства от kj-1 до kj прирост расстоянии достигается путем добавления мерности для каждого из ![]() сигналов, что проявляется на шкале амплитуд.
сигналов, что проявляется на шкале амплитуд.
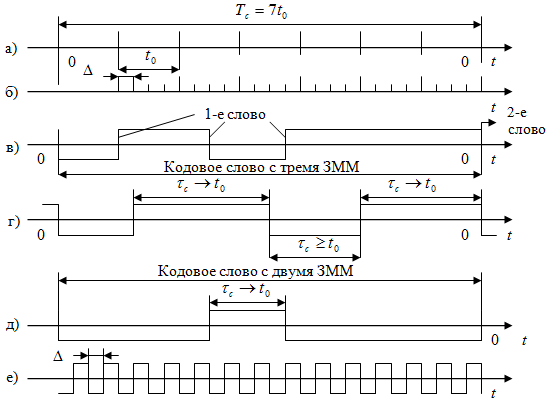
Рассмотрим принцип построения таймерных сигналов (ТСК), который заключается в следующем. Сигнальный алфавит бинарных ТСК формируется на интервале времени Tc=mt0 (t0 – величина, обратная полосе пропускания канала ΔF) при базовом элементе Δ (Δ=t0/s s ∈ 1;2;3;…k – целые числа) (рис. 2).
Тогда на интервале Tc=mt0 расположено n=t0·s точек.
Из всего множества 2n возможных на интервале времени Tc сигналов разрешенными считаются только те, в которых соседние значащие моменты модуляции (ЗММ) отстоят друг от друга на время, не меньшее, чем t0. Это условие обеспечивает минимум межсимвольных искажений. Информация о передаваемом сообщении, переносимая ТСК, содержится в номере временной позиции, занимаемой ЗММ, на интервале Тk выраженном в значениях D. Так как величина D<t0, то увеличение пропускной способности возможно, если число реализаций сигнала на интервале (mt0) больше 2m. Можно показать, что при заданном s(s=t0/D) на интервале т единичных элементов мощность размещенного сигнального алфавита бинарных ТСК определяется как [3]
где i – число информационных ЗММ в сигнале. Среди разрешенных сигналов могут быть реализации с одним ЗММ, двумя, тремя и т.д. С максимальным числом моментов модуляции т возможна только одна реализация.
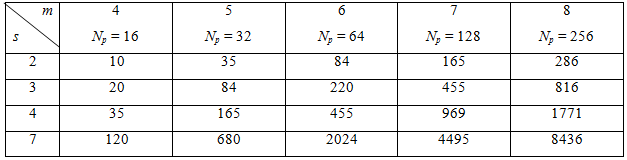
Для примера в табл. 1 приведено количество реализаций ТСК и среднее значение ЗММ для некоторых величин Tc=mt0·S; N=2m.
Рис. 2 - Формирование сигнального алфавита бинарных ТСК на интервале времени Tc=mt0 при базовом элементе Δ
Таблица 1 - Количество реализаций i = 3; s Î 2, 3, 4; m Î (4¸8) t0
Как видно из табл. 1 на одном и том же интервале реализации можно синтезировать на много большее число реализаций: так при m = 8 для s = 2 можно передавать 286 кодовых слов, каждое из которых может передать 8 бит информации или при s = 7 – 8436 кодовых слова, каждое из которых может передать более 13 бит информации.
Следует отметить, что при i = 5, s = 7, m = 8 [3] можно реализовать 65780 сигнальных конструкций, каждое из которых может передавать более 16 бит информации
Литература
- Латхи Б.П. Системы передачи информации. – М.: Связь. – 1971.
- Боккер П. Передача данных. Том 1. Основы. – М.: Связь, 1980 – 264 с.
- Сукачев Э.А. Новая форма представления селективных сигналов для телекоммуникационных систем // Працi УНДIРТ. – Одеса: вид. УНДIРТ. – 1998. № 2 (14). – С. 98-102.
References
- Lathi B.P. Information transmission systems. - M .: Communication. - 1971.
- Bokker P. Data transmission, Volume 1. Fundamentals. - M .: Communications, 1980 - 264 p.
- Sukachev E.A. The new format of selective signals for telecommunication systems // Pratsi UNDIRT. - Odessa: appearance. UNDIRT. - 1998. № 2 (14). - P. 98-102.