СБОРКА И МОНТАЖ СУДОВЫХ СБОРОЧНО-МОНТАЖНЫХ ЕДИНИЦПО МЕТОДУ РАЗОВОЙ СБОРКИ НА ОСНОВЕ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ПРОЦЕССОВ
Петров Н.В.
Кандидат технических наук, ОАО «Центр технологии судостроения и судоремонта»
СБОРКА И МОНТАЖ СУДОВЫХ СБОРОЧНО-МОНТАЖНЫХ ЕДИНИЦПО МЕТОДУ РАЗОВОЙ СБОРКИ НА ОСНОВЕ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ПРОЦЕССОВ
Аннотация
Предложен экспериментальный метод для моделирования технологических процессов при наличии зависимости между определяющими факторами.
Разработаны технологии сборки и монтажа судовых сборочно-монтажных единиц(СМЕ)по методу разовой сборки, а именно путем однократного воздействия на отжимные приспособления, динамометры.
Технологии обеспечивают снижение трудоемкости и продолжительности сборочных и монтажных работ, раннее выявление и устранение нарушений собираемости и коллизий и др.
Ключевые слова: сборочно-монтажные единицы, центровка, базирование, регулирование опорных нагрузок, диагностирование, изгибающий момент и поперечная сила.
Petrov N.V.
Candidate of Engineering Sciences, JSC «Shipbuilding & Shiprepair Technology Center»
ASSEMBLY AND INSTALLATION OF SHIP SUB UNITS USING SINGLE ASSEMBLY METHOD BASED ON MATHEMATIC MODELING
Abstract
Proposed here is experimental method for modeling of technological procedures used with dependencies between defining factors.
Reviewed are technologies for assembly of ship sub-units (SSU) using single assembly method, i.e. single exposure at pulling mechanisms and dynamometers.
These technologies help to decrease labor intensity and duration of assembly and installation works, early detection and removal of assembly errors, collisions, etc.
Keywords: sub units, center adjustment, referencing, support loads control, diagnostic, bending moment and transverse force.
При разработке технологических процессов сборки и монтажа СМЕнеобходимо установить значительное количество требований, среди которых могут быть выделены:
последовательность выполнения отдельных операций;
способы выполнения отдельных операций;
требования к технологическим режимам или условиям выполнения операций;
требования к показателям точности операций.
Наиболее распространёнными средствами, используемыми при разработке технологических процессов, являются методы расчёта размерных цепей.
Применение методов расчета размерных цепей предполагает известность аналитических зависимостей между замыкающим и составляющими звеньями размерной цепи. Расчеты позволяют определить номинальные значения и допуски размеров, составляющих размерную цепь.
Однако, при разработке технологических процессов сборки и монтажа судового оборудванияприходится иметь дело с процессами, для которых аналитические зависимости не известны, или при неполном знании происходящих в них явлениях.
Примером таких процессов, в частности, можетслужить регулирование опорных нагрузок СМЕ. После установки СМЕ на стенде или на судовом фундаменте на динамометрах или гидродомкратах, исходя из условий равновесия, значения опорных нагрузок могут быть описаны системой из трех линейных уравнений. Но, даже имея формальное описание процесса регулировки опорных нагрузок в виде системы из трех уравнений, отсутствие знаний жесткостных характеристик несущей конструкции не позволит рассчитать опорные нагрузки.
Именно по этим причинам для описания процесса регулирования опорных нагрузок используется табличный способ задания функциональной зависимостина основе составления формуляров нагрузок.
Более широкие возможности представляют метод планирования эксперимента [1].В основу метода заложено представление объекта исследования в виде кибернетической схемы - «черного ящика»(рисунок 1), имеющего входные переменные (факторы) Рi(i=1…n) и выходные (целевые функции или функциональные параметры)Z.Применение многофакторногоэксперимента позволяет описать объект исследования математической моделью, связывающей функциональные параметры с факторами, например, в виде линейного уравнения (1)

Рис. 1 – Представление объекта исследования в виде «черного ящика» для независимых факторов
Использование понятия «черный ящик» позволяет рассматривать СМЕ как объект регулирования, а процессы сборки и монтажа – как процессы регулирования входных переменных при определённых ограничениях с целью обеспечения заданного значения функционального параметра.
Возвращаясь к предыдущему примеру, следует отметить, что процесс регулирования опорных нагрузок, по воспроизводимости результатов и частично по возможности управления факторами отвечает требованиям, предъявляемым к факторам при планировании эксперимента. При регулировании опорных нагрузок (управлении) возможность поддержания фактора на постоянном уровне обеспечивается только при регулировке одного отдельного динамометра. В дальнейшем опорная нагрузка на этом динамометре будет изменяться за счет регулировки других динамометров.
Ограничения по применению методов планированного эксперимента появляются при рассмотрении требований к совокупности факторов. В монографии[1] это требование сформулировано в следующем виде: « При планировании эксперимента важна независимость факторов, т.е. возможность установления фактора на любом уровне вне зависимости от уровней других факторов. Если это условие невыполнимо, то невозможно планировать эксперимент».
Если обратиться к регулированию опорных нагрузок, то увидим нарушение требования независимости факторов. Взаимное влияние нагрузок динамометров выражается в том, что при изменении нагрузки на одном из динамометров одновременно происходит изменение нагрузок на других динамометрах. Это влияние проявляется более заметно на динамометрах расположенных рядом с регулируемым динамометром и по мере удаления от него ослабевает.
Наличие взаимной зависимости существенно усложняет процесс регулировки динамометров и обуславливает выполнение регулировки по методу «проб и ошибок», а именно, на основе последовательных изменений значений регулируемых параметров и субъективной оценке следующего шага регулировки по изменению функционального параметра.
Откуда следует, что для описания процессов сборки и монтажа СМЕ необходима разработка экспериментального метода для моделирования процессов при наличии зависимости между определяющими факторами.
Рассмотрим возможные методы моделирования процессов с зависимыми факторами на примере регулирования опорных нагрузок СМЕ.
Для определенности задачи регулирования опорных нагрузок примем следующее ограничение - регулирование динамометров выполняется, последовательно начиная с динамометра с порядковым номером 1 до n.Для характеристики технологических процессов, в которых регулирование опорных нагрузок или перемещений в опорных точках выполняется путем одноразового воздействия на динамометр или отжимное приспособление или иначе за один их обход в дальнейшем будем применять термин разовая сборка. Например, центровка по методу разовой сборки и т.д.
Принятое ограничение позволяет ввести для описания процесса регулирования новую переменную xi , под которой в дальнейшем будем понимать значение изменения нагрузки от значения, полученного при выполнении предыдущей операции. Для примера значения изменений будут составлять: для динамометра с номером 1 – изменение от начального значения X10до значения X10+X1, для динамометра с номером i -изменение от Xit, полученного после регулировки динамометров с номерами от 1 до (i-1) до значения Xit+Xi. В дальнейшем новую независимую переменную будем называть технологическим параметром процесса регулирования.
Исходя из зависимости функционального параметра от значений опорных нагрузок ![]()
![]()
зависимость функционального параметра от значений технологических параметров может быть представлена в виде
![]()
С другой стороны зависимость опорных нагрузок от значений технологических параметров может быть представлена уравнениями вида
![]()
После разложения функций (3), (4) в ряд Тейлора получим систему линейных уравнений позволяющую моделировать процессы при наличии зависимости между определяющими факторами
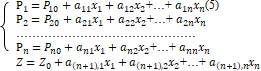
где ![]() - значения опорных нагрузок и функционального параметра перед началом регулирования;
- значения опорных нагрузок и функционального параметра перед началом регулирования;
![]() – коэффициенты модели, соответствующие значениям частных производных нагрузки – ого динамометра по – ому технологическому параметру
– коэффициенты модели, соответствующие значениям частных производных нагрузки – ого динамометра по – ому технологическому параметру ![]()
![]() – коэффициенты модели, соответствующие значениям частных производных функционального параметра по – ому технологическому параметру
– коэффициенты модели, соответствующие значениям частных производных функционального параметра по – ому технологическому параметру ![]()
Следует отметить ряд особенностей полученной математической модели.
Для объектов с зависимыми факторами в качестве входных переменных используются технологические параметры, а зависимые факторы переносятся к выходным данным и рассматриваются как новые функциональные параметры (рисунок 2).

Рисунок 2 – Представление объекта исследования в виде «черного ящика» для зависимых факторов
Зависимость (2) между функциональным параметром Z и зависимыми факторами Р1… Рnзадается в неявном виде через новые переменные - технологические параметры Х1… Хn.
Значения коэффициентов модели при i=j равны 1. В случае если принять, что факторы независимы, т.е. ( ; , то система уравнений приводится к виду, получаемому методами планирования эксперимента. Это показывает, что полученная модель является более общей и может применяться для исследования объектов, как с зависимыми, так и с независимыми факторами.
Отличие сравниваемых методов заключается в том, что при проведении эксперимента для получения математической модели для независимых факторов производят одновременное варьирование всеми переменными по определенному плану эксперимента, а при наличии зависимости факторов одновременное варьирование переменных не выполнить.
При применении методов планирования эксперимента возможна как раздельная, так и одновременная регулировка входных переменных. При использовании моделей для зависимых факторов – только раздельная последовательная регулировка. Это отличие определяется принятым выше ограничением по последовательному выполнению регулировки.
Рассмотрим конкретные примеры моделирования процессов сборки и монтажа СМЕ на основе предложенного экспериментального метода.
1. Регулирование СМЕ по функциональным параметрам.Процессы регулирования по функциональным параметрам в механомонтажном производстве в настоящее время не применяются. В машиностроении наметилась тенденция по развитию процессов сборки и монтажа механизмов по комплексным показателям качества наиболее полно связанным с показателями функционирования механизмов.
Так, разработан процесс сборки крупных многоузловых машин с контролем потерь мощности [2]. Способ реализован на основе регулировки положения опор в зависимости от тока приводного двигателя.
Математическая модель процесса регулирования по функциональным параметрам соответствует модели, полученной при рассмотрении процессов регулирования опорных нагрузок с контролем функционального параметра в виде переопределённой системы линейных уравнений (5).
В зависимости от решаемой задачи в качестве функционального параметра могут применяться комплексные показатели качества, например потери мощности, значения вибрации в заданных точках и др., в качестве технологических параметров – значения изменений опорных нагрузок или перемещения СМЕ в опорных точках и др.
2. Регулирование опорных нагрузок амортизированных СМЕ.Для амортизированных СМЕ, как правило, функциональный параметр не устанавливается. Это позволяет упростить математическую модель (5) за счет исключения выражения для функционального параметра. В результате математическая модель регулирования опорных нагрузок приводится к квадратной системе линейных уравнений вида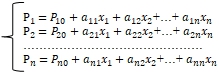 (6)
(6)
Обозначения переменных приведены выше.
Базирование СМЕ.
Сложность процессов базирования современных СМЕ обуславливается значительным количеством (20 – 40) контролируемых параметров.
При базировании в качестве выходных переменных следует принять значения монтажных и амортизационных зазоров … , в качестве входных – технологические параметры процесса базирования … . По аналогии с процессами регулирования опорных нагрузок технологические параметры будут определять перемещения СМЕ в заданной опорной точке от значения, полученного при выполнении предыдущей операции.
Исходя из принятого представления СМЕ как объекта регулирования, математическая модель процесса базирования СМЕ может быть представлена в виде переопределённой системы линейных уравнений
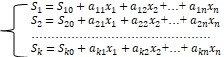 (7)
(7)
Значения индексов системы уравнений: ![]() , что показывает необходимость минимизации количества контролируемых параметров процесса.
, что показывает необходимость минимизации количества контролируемых параметров процесса.
Центровка механизмов по изломам и смещениям.
Как и при базировании механизмов при центровке решается задача установки механизмов в положение заданное монтажным чертежом. В общем случае при центровке в качестве контролируемых параметров применяют изломы и смещения в соединениях валов и значения монтажных и амортизационных зазоров ![]() .
.
Математическая модель процесса центровки аналогична модели для процесса базирования (7) и определяется следующей переопределенной системой линейных уравнений
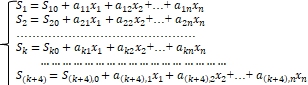 (8)
(8)
Экспериментальное определение изгибающего момента и поперечной силы в соединениях валов центруемых механизмов.
Стремление поставщиков повысить надежность эксплуатации механизмов стимулировали развитие методов, позволяющих ограничивать нагрузки на подшипники механизма и напряжения в валах посредством нормирования значений изгибающего момента и поперечной силы в соединениях валов центруемых механизмов. Основой для разработки таких методов могут служить известные методы сопротивления материалов [3].
Показателен опыт фирмы «MAN-B&W Diesel A|S» [4]. На основе расчетов методом конечных элементов установлены предельные значения изгибающего момента и поперечной силы для дизелей производимых фирмой. Одновременно приведены данные по допускаемым нагрузкам на подшипники и показатели жесткости вала дизеля по отношению к действию изгибающего момента и поперечной силы, на основе которых могут рассчитываться параметры центровки дизелей.
Учитывая сложную конструкцию роторов и валов современных машин и механизмов, в том числе наличие насадных деталей, сложную геометрическую форму, переменное по длине сечение при использовании расчетных методов приходится вводить ряд допущений, которые снижают точность расчетов. Представляется целесообразным наряду с расчетными методами использовать также и экспериментальные методы.
Возможность экспериментального определения параметров изгибающего момента и поперечной силы имеется до сборки механизма, а именно после окончательного изготовления ротора или вала механизма и может выполняться на стенде.
На основе представления вала механизма как объекта регулирования математическая модель процесса регулирования нагрузок на подшипники может быть представлена в виде переопределенной системы линейных уравнений
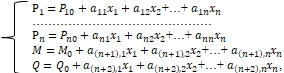 (9)
(9)
которая в неявном виде устанавливает зависимость изгибающего момента и поперечной силы от значений нагрузок на подшипники … (n – количество подшипников).
Анализ полученных математических моделей позволяет наметить следующие направления совершенствования процессов сборки и монтажа СМЕ:
уменьшение количества регулировок и соответственно выполнения работ по методу разовой сборки;
уменьшение количества контролируемых параметров;
выполнение оптимального регулирования входных параметров;
обнаружение нарушений собираемости и коллизий;
совмещение работ;
автоматизация процессов сборки и монтажа.
Основой для реализации представленных направлений являются следующие положения.
Математические модели (5…9) позволяют определить совокупность технологических параметров … , отвечающих требованиям минимально возможного количества регулировок СМЕ при реализации конкретного технологического процесса, а именно обеспечить однократное воздействие на отжимное приспособление или динамометр.
Возможность идентификации процессов сборки и монтажа системами линейных уравнений позволяет сократить количество регулируемых параметров на основе объединения их в группы и соответственно уменьшить трудоемкость и продолжительность работ.
Для процессов регулирования СМЕ по функциональным параметрам правомерна постановка задачи обеспечения оптимального значения функционального параметра при ограничениях допустимых значений опорных нагрузок или перемещений. Определение значений технологических параметров может выполняться методами линейного программирования;
При регулировании опорных нагрузок амортизированных СМЕ математическая модель представлена квадратной системой линейных уравнений, которая может быть решена прямыми или итерационными методами (Ильин В.А., 2004, 296 с);
Для процессов базирования СМЕ и центровки механизмов решение переопределённых систем уравнений также может выполняться прямыми или итерационными методами. Однако при применении расчетных методов может возникнуть ряд препятствий. В связи высокими массогабаритными характеристиками при монтаже СМЕ наблюдаются коллизии и нарушения собираемости между элементами СМЕ и корпусными конструкциями. Наличие последних будет приводить к нарушениям совместности системы уравнений. Это в свою очередь не позволит определить технологические параметры процесса и свидетельствует о целесообразности разработки методов, обеспечивающих локализацию нарушений собираемости и коллизий на основе интерактивного взаимодействия производителя работ с моделью.
Блок-схема функционирования, визуальное представление интерактивных моделей и методы их применения для выявления и устранения коллизий и нарушений собираемости рассмотрены в [6],[7].
При обосновании моделей центровки механизмов (8) в рассмотрение намеренно включены все факторы, реально контролируемые при выполнении технологического процесса, что привело к ее усложнению. Это позволяет достичь качественных изменений процесса центровки по сравнению с традиционными методами центровки по базовому механизму. В первую очередь изменения касаются возможности совмещения операций установки центруемых механизмов и их выполнению по методу, который может быть охарактеризован, как совместная центровка. Следует отметить, что при исключении из модели (8) значений перемещений в опорных точках смежного механизма математическая модель упрощается и приводится элементарной зависимости используемой при традиционных методах центровки по базовому механизму. При этом соответственно исчезает возможность выполнения совместной центровки. Это свидетельствует о том, что модель (8) является более общей. На основе предложенного метода разработаны математические модели для совместной центровки двух-, трех- и многомашинных агрегатов, центровка с контролем отклонений от горизонтальности и электрических машин с выносными подшипниками, что рассмотрено в статье [6].
При моделировании процессов центровки по изгибающему моменту и поперечной силе технологические параметры имеют второстепенное значение и могут использоваться для снижения трудоемкости экспериментальных работ по определению параметров центровки. Более важной в данном случае является возможность определения на основе системы уравнений допусков параметров центровки и использование уравнений в качестве диагностической модели для выполнения безразборной диагностики состояния центровки [8].
Применение математических моделей обеспечивает возможность автоматизации процессов сборки и монтажа СМЕ двумя методами:
на основе компьютерного управления параметрами процесса;
на основе создания системы автоматического регулирования.
В первом случае автоматизация процесса достигается на основе реализации следующего алгоритма. При воздействии возмущения измеряют текущие значения регулируемых параметров (при регулировании опорных нагрузок согласно системы уравнений(6) – переменные ). По системе (6) рассчитывают технологические параметры. Под управлением процессора выполняют поочередные изменения опорных нагрузок. Момент времени, в который необходимо выполнить регулировку опорных нагрузок, может быть установлен на основе ограничения отклонения текущего значения нагрузки от заданного.
Применение автоматического регулирования параметров СМЕ позволяет совместить, а именно, одновременно выполнять два процесса, например, базирование и регулирование опорных нагрузок или центровку и регулирование опорных нагрузок.
Процесс может быть реализован на основе применения двух групп гидродомкратов. Первой – предназначенной для базирования или центровки и второй – для регулирования опорныхнагрузок. При этом последняя группа гидродомкратов должна работать в режиме поддержания постоянных опорных нагрузок.
Литература
- Адлер, Ю. П. и др.Планирование эксперимента при поиске оптимальных условий. М. : Наука, 1976, 279с.
- Жабин А.И., Бровман М.Я. Новый способ сборки крупных многоузловых агрегатов машин"Вестник машиностроения", №4. 1983 r., С.52-55.
- Беляев Н.М.Сопротивление материалов. Москва : "Наука", 1976, 607 с.
- Jensen, M.“Investigation of alignment difficulties in ships with heavy shafting”,. Copenhagen : MAN-B&W Diesel A|S, 1985.
- ИльинВ.А., ПозднякЭ.Г.,.Линейная алгебра:Учебник для вузов-6-ое издание. Москва : Физматлит, 2004, 296 с.
- Петров Н.В.Совместная центровка вспомогательных механизмов. Вестник технологии судостроения и судоремонта. №18. Санкт- Петербург : ОАО "ЦТСС", 2010, С. 102-106.
- Петров Н.В.Базирование крупногабаритных сборочно-монтажных единиц по методу разовой сборки. Судостроение, №3. Санкт-Петербург : ОАО "ЦТСС", 2012. С. 56-58. ISSN0039-4580.
- Петров Н.В.Безразборное диагностирование центровки по параметрам силового взаимодействия механизмов. Морской вестник .№1. Санкт-Петербург : "Морвест", 2013. ISSN 1812-3694. С. 55-57.
