ПРУЖИННЫЙ АККУМУЛЯТОР ПЕРЕМЕННОЙ КОНФИГУРАЦИИ С ГИБКИМ ЗВЕНОМ
Миничев А.В.
ORCID: 0000-0002-3770-8155, инженер-конструктор 2 категории,
АО «Центральное конструкторское бюро машиностроения»
ПРУЖИННЫЙ АККУМУЛЯТОР ПЕРЕМЕННОЙ КОНФИГУРАЦИИ С ГИБКИМ ЗВЕНОМ
Аннотация
В данной статье рассматривается пружинный аккумулятор переменной конфигурации, предназначенный для применения в многопозиционном пружинном приводе с поступательным движением выходного звена, приводятся его геометрические, динамические и силовые характеристики, а также варианты компоновки. Кроме того, представлены выражения, позволяющие рассчитать требуемые значения жесткости пружин и межосевого расстояния исходя из известных параметров технологической операции. Приведённая в статье информация может быть использована при проектировании аккумулятора переменной конфигурации с гибким звеном.
Ключевые слова: пружинные аккумуляторы, многопозиционный привод, линейный привод, механическая энергия, рекуперация.
Minichev A.V.
ORCID: 0000-0002-3770-8155, Design engineer of II category,
JSC "Central Design Bureau of Mechanical Engineering"
SPRING ACCUMULATOR OF VARIABLE CONFIGURATION WITH FLEXIBLE LINK
Abstract
This article considers a spring-loaded, variable configuration accumulator intended for use in a multi-position spring drive with translational motion of the output link, it’s geometric, dynamic and power characteristics, as well as layout options are given. In addition, formulas are presented that allow you to calculate the required values of spring stiffness and distance between axes based on known parameters of the process operation. The information in the article can be used to design a variable configuration accumulator with a flexible link.
Keywords: spring accumulators, multi-position drive, linear drive, mechanical energy, recuperation.
Известны приводы с рекуперацией энергии для возвратно-поступательного [1, С. 91], [3, С. 68-76], [8], [10, С. 1-5] и возвратно-качательного движения [3, С. 10], [4, С. 29], [5, С. 217, 224], [6, С. 5, 14], [7, С. 499-509]. Многопозиционность в приводах с рекуперацией обеспечивается, как правило, использованием дифференциальных пружинных аккумуляторов и групп управляемых упоров [5, С. 224, 227, 232], [6, С. 14-15, 17, 21]. В работе [5, С. 351-352] рассмотрены пружинные приводы, построенные с использованием гибкого звена. В работе [2, С. 489-503] рассмотрен нелинейный пружинный аккумулятор переменной конфигурации, предназначенный для использования в многопозиционном пружинном приводе с поступательным движением выходного звена, К недостаткам аккумулятора, рассмотренного в работе [2, С. 489-503] можно отнести зависимость времени перемещения выходного звена от величины заданного перемещения.
Рассмотрим пружинный аккумулятор переменной конфигурации, построенный с использованием троса. Схема пружинного аккумулятора представлена на рис. 1.
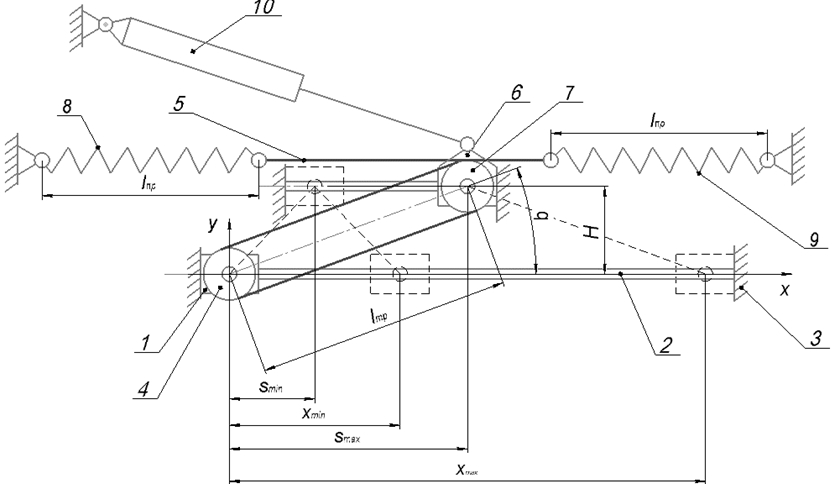
Рис. 1 – Пружинный аккумулятор переменной конфигурации
Выходное звено 1 установлено на направляющей 2 с возможностью линейного перемещения. Направляющая 2 установлена на корпусе 3. Выходное звено 1 оснащено блоком 4. Также аккумулятор содержит каретку 6, оснащённую блоком 7. Выходное звено 1 соединяется с кареткой 6 посредством троса 5, огибающего блоки 4 и 7 и соединяющегося концами с пружинами 8 и 9. Вторые концы пружин 8 и 9 соединяются с корпусом 3. Положение каретки 6 задаётся приводом 10, установленным на корпусе 3.
Пружинный аккумулятор характеризуется следующими величинами:
х – координата выходного звена, ![]() – значения минимального и максимального перемещения выходного звена;
– значения минимального и максимального перемещения выходного звена;
s – координата каретки, ![]() – минимальное и максимальное значение координаты каретки;
– минимальное и максимальное значение координаты каретки;
Н – межосевое расстояние;
С – жесткость пружины;
![]() – длина пружины,
– длина пружины, ![]() – минимальная и максимальная длины пружины,
– минимальная и максимальная длины пружины, ![]() – удлинение пружины;
– удлинение пружины;
q – угол приложения силы к выходному звену.
Поскольку параметры ![]() определяются технологической операцией, а коэффициент удлинения пружины
определяются технологической операцией, а коэффициент удлинения пружины ![]() может быть принят в пределах 2…8, определим требуемое удлинение пружин. Удлинение пружин
может быть принят в пределах 2…8, определим требуемое удлинение пружин. Удлинение пружин ![]() соответствует расстоянию между осями блоков 4 и 7 и вычисляется как:
соответствует расстоянию между осями блоков 4 и 7 и вычисляется как:
![]() (1)
(1)
Приведём выражение (1) к виду:
![]() (2)
(2)
Тогда безразмерная величина![]() , характеризующая удлинение пружины, определяется как:
, характеризующая удлинение пружины, определяется как:
![]() (3)
(3)
Если пренебречь работой диссипативных сил, то для рассматриваемого аккумулятора справедливо выражение:
![]() (4)
(4)
Где ![]() – требуемое перемещение выходного звена.
– требуемое перемещение выходного звена.
С учётом (4) максимальное удлинение пружины ![]() определяется согласно выражению:
определяется согласно выражению:
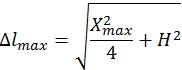 (5)
(5)
Межосевое расстояние Н может быть выбрано из диапазона H>d где d – диаметр блоков 4 и 7.
Приведём выражение (5) к виду (6), тогда безразмерная величина, характеризующая максимальное удлинение пружины![]() , определяется как:
, определяется как:
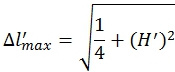 (6)
(6)
Преобразуя (5) c использованием определения коэффициента удлинения, получаем выражение для минимальной длины пружины:
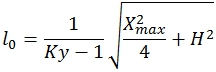 (7)
(7)
Приведём выражение (7) к виду (2), тогда безразмерная величина![]() , характеризующая минимальную длину пружины:
, характеризующая минимальную длину пружины:
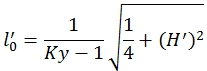 (8)
(8)
Максимальная длина пружин определяется как:
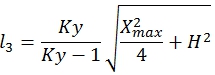 (9)
(9)
Приведём выражение (9) к виду (2), тогда безразмерная величина ![]() , характеризующая максимальную длину пружин:
, характеризующая максимальную длину пружин:
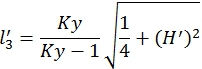 (10)
(10)
Угол приложения силы пружин к выходному звену q определяется через тригонометрические функции:
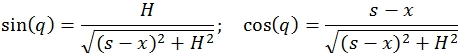 (11)
(11)
Сила ![]() , действующая на выходное звено со стороны пружины, выражается как:
, действующая на выходное звено со стороны пружины, выражается как:
![]() (12)
(12)
Максимальное усилие пружины ![]() определяется согласно следующему выражению:
определяется согласно следующему выражению:
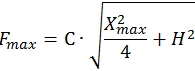 (13)
(13)
Выражения для х и у составляющих силы, действующей на выходное звено, имеют вид:
![]() (14)
(14)
Безразмерная величина ![]() , характеризующая силу, действующую на выходное звено со стороны пружины, может быть определена согласно следующему выражению:
, характеризующая силу, действующую на выходное звено со стороны пружины, может быть определена согласно следующему выражению:
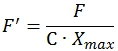
Из выражения (14) видно, что составляющая силы вдоль оси y постоянна. Таким образом, данный аккумулятор может обеспечивать разгрузку направляющей от силы тяжести, действующей со стороны выходного звена. В этом случае межосевое расстояние определяется как:
![]() (15)
(15)
m – масса выходного звена, g - ускорение свободного падения.
Потенциальная энергия аккумулятора определяется как
![]() (16)
(16)
Безразмерная величина ![]() , характеризующая энергию аккумулятора, может быть выражена следующим образом:
, характеризующая энергию аккумулятора, может быть выражена следующим образом:
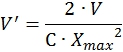 (17)
(17)
Подставляя (16) в (17), получаем:
![]() (18)
(18)
Максимальная потенциальная энергия пружины ![]() определяется согласно следующему выражению:
определяется согласно следующему выражению:
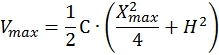 (19)
(19)
Аналогично [2] рассмотрим уравнение полной механической энергии системы:
![]() (20)
(20)
где V – текущее значение потенциальной энергии пружины; ![]() – потенциальная энергия пружины в начальный момент времени; Е – кинетическая энергия выходного звена;
– потенциальная энергия пружины в начальный момент времени; Е – кинетическая энергия выходного звена; ![]() – работа диссипативных сил на рассматриваемом перемещении.
– работа диссипативных сил на рассматриваемом перемещении.
Потенциальная энергия пружины определяется согласно выражению (16). Кинетическая энергия определяется как:
![]() (21)
(21)
Скорость выходного звена ![]() выражается как:
выражается как:
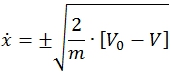 (22)
(22)
Пренебрегая работой диссипативных сил, подстановкой (16), (20) в (21) получаем выражение для определения скорости выходного звена:
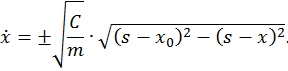 (23)
(23)
Безразмерная величина ![]() , характеризующая скорость выходного звена, определяется следующим образом:
, характеризующая скорость выходного звена, определяется следующим образом:
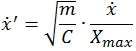 (24)
(24)
Согласно работе [9, С. 39], время перемещения выходного звена определяется как:
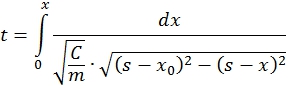 (25)
(25)
Безразмерная величина ![]() , характеризующая время перемещения выходного звена, определяется как:
, характеризующая время перемещения выходного звена, определяется как:
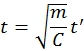 (26)
(26)
Подставляя (25) и (4) в (26), и считая ![]() получаем:
получаем:
![]()
Таким образом, данный аккумулятор обладает постоянным временем перемещения выходного звена, не зависящим от положения центра колебаний.
Подставляя полученное значение ![]() в (26), выразим жесткость пружины исходя из требуемого времени перемещения выходного звена:
в (26), выразим жесткость пружины исходя из требуемого времени перемещения выходного звена:
![]() (27)
(27)
Подставляя (27) в (15), выражение для определения величины H при заданном быстродействии привода:
![]() (28)
(28)
Тогда минимальная длина пружины c учётом выбора H из соображений разгрузки направляющей определяется как:
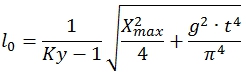 (29)
(29)
Подставляя (27) и (28) в (18), получаем выражение для максимальной потенциальной энергии ![]() :
:
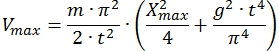 (30)
(30)
Максимальное усилие пружины ![]() определяется как:
определяется как:
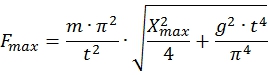 (31)
(31)
Заключение. В работе приведены зависимости, описывающие геометрические характеристики пружинного аккумулятора переменной конфигурации, предназначенного для применения в конструкции многопозиционного привода с поступательным движением выходного звена. Получены выражения, позволяющие определить значения таких конструктивных параметров аккумулятора, как межосевое расстояние Н, жесткость пружины , исходя из заданных максимального и минимального перемещения выходного звена, времени перемещения, перемещаемой массы.
Полученные выражения могут быть использованы при проектировании пружинного аккумулятора переменной конфигурации.
Список литературы / References
- Миничев А. В. – Разработка и исследование пружинного привода / А. В. Миничев // Неделя науки СПбПУ: Материалы научной конференции с международным участием. Лучшие доклады. – СПб.: Изд-во Политехн. ун-та, 2016. – С. 91-95.
- Миничев А.В. – Исследование геометрических характеристик пружинного аккумулятора переменной конфигурации / А. В. Миничев // Современное машиностроение: Наука и образование: материалы 6-й Международной научно-практической конференции. – СПб.: Изд-во Политехн. ун-та, 2017. – С. 489-503.
- Жавнер В. Л. Рекуперативные приводы для цикловых перемещений: Учебное пособие / В. Л. Жавнер, О. Н. Мацко, М. В. Жавнер - Palmarium Academic Publishing: Saarbrucken, 2014. – 90 с.
- Глушков А. А. Исследование и разработка быстродействующих поворотных цикловых приводов колебательного типа: дисс. ... канд. техн. Наук : 05.02.02 : защищена 27.12.06 / Глушков Андрей Алексеевич. - Владимир, ВлГУ, 2006. – 148 с.
- Корендясев А. И. Манипуляционные системы роботов. / А. И. Корендясев, Б. Л. Саламандра, Л. И. Тывес и др. – М.: Машиностроение. – 1989. – 470 с.
- Корендясев А. И. Теоретические основы робототехники. В 2 кн. Т. 2. / А. И. Корендясев, Б. Л. Саламандра, Л. И. Тывес и др. М.: Наука. 2006.– 376 с.
- Пелупесси Д. С. Пружинные аккумуляторы для шаговых приводов / Д. С. Пелупесси, М. В. Жавнер // Современное машиностроение. Наука и образование: Материалы V Междунар. науч. -практ.конф. –СПб.: Изд-во Политехн. ун-та,–2016. – С.499-509.
- Патент РФ №158169. Рекуперативный привод / Миничев А.В., Мацко О.Н.; Опубл. 20.12.15, Бюл. № 35.
- Ландау Л. Д. Теоретическая физика: Учеб. пособие. – В 10-ти т. Т. 1. – Механика. / Л. Д. Ландау, Е. М. Лифшиц– 4-е изд., испр. – М.: Наука. Гл. ред. физ.-мат. лит., 1988. – 216 с.
- Zhavner V.L. Spring drives for reciprocal motion, / V.L. Zhavner, O.N. Matsko // Journal of Machinery Manufacture and Reliability, 2016, No.1, pp.1-5.
Список литературы на английском языке / References in English
- Minichev A. V. Razrabotka i issledovanie pruzhinnogo privoda [Development and research of a spring drive] / A. V. Minichev // Nedelya nauki SPbPU: Materialy nauchnoy konferencii s mezhdunarodnim uchastiem [Week of Science SPbPU: Proceedings of a scientific conference with international participation. Best reports]. – SPb.: Izdatelstvo Polytehnicheskogo universiteta. 2016. – P. 91-95. [in Russian]
- Minichev A. V. Issledovanie geometricheskih harakteristik pruzhinnogo akkumulatora peremennoi konfiguracii [Investigation of the geometric characteristics of a spring accumulator] / A. V. Minichev // Sovremennoe mashinostroenie: Nauka i obrazovanie: materialy 6-oi nauchno-prakticheskoy konferencii [Modern Engineering: Science and Education: Materials of the 6th International Scientific and Practical Conference]. – SPb.: Izdatelstvo Polytehnicheskogo universiteta. 2016. – P. 489-503. [in Russian]
- Zhavner V. L. Rekuperativnye privody dlja ciklovyh peremeshhenij: Uchebnoe posobie [Recuperative drives for reciprocal motion: Textbook] / V. L. Zhavner, O. N. Macko, M. V. Zhavner - Palmarium Academic Publishing: Saarbrucken, 2014. – 90 p. [in Russian]
- Glushkov A. A. Issledovanie i razrabotka bystrodejstvujushhih povorotnyh ciklovyh privodov kolebatel'nogo tipa [Research and development of high-speed rotary reciprocal drives of oscillatory type]: diss. ... PhD in Engineering Sciences : 05.02.02 : defense of the thesis 27.12.06 / Glushkov Andrej Alekseevich. - Vladimir, VlGU, 2006. – 148 p. [in Russian]
- Korendjasev A. I. Manipuljacionnye sistemy robotov [Manipulative systems of robots] / A. I. Korendjasev, B. L. Salamandra, L. I. Tyves and other. – M.: Mashinostroenie. – 1989. – 470 p. [in Russian]
- Korendjasev A. I. Teoreticheskie osnovy robototehniki [Theoretical Foundations of Robotics]. In 2 h, the P. 2. / A. I. Korendjasev, B. L. Salamandra, L. I. Tyves and other. M.: Nauka. 2006. – 376 p. [in Russian]
- Pelupessi D. S. Pruzhinnye akkumuljatory dlja shagovyh privodov [Spring accumulators for stepper drives] / D. S. Pelupessi, M. V. Zhavner // Sovremennoe mashinostroenie. Nauka i obrazovanie: Materialy V Mezhdunar. nauch. -prakt.konf. [Modern Engineering: Science and Education: Materials of the 5th International Scientific and Practical Conference]. –SPb.: Izdatelstvo Polytehnicheskogo universiteta. –2016. – Pp. 499-509 [in Russian]
- Patent of the Russian Federation No. 158169. Rekuperativnyj privod [Recuperative drive] / Minichev A. V., Matsko O. N.; Published on 20.12.15, bulletin № 35. [in Russian]
- Landau L.D. Teoreticheskaja fizika: Ucheb. posobie. [Theoretical Physics: a Tutorial] – In 10 h, the P. 1. – Mehanika. / L. D. Landau, E. M. Lifshic– 4th revised edition. – M.: Nauka. Gl. red. fiz.-mat. lit., 1988. – 216 p. [in Russian]
- Zhavner V.L. Spring drives for reciprocal motion, / V. L. Zhavner, O. N. Matsko // Journal of Machinery Manufacture and Reliability, 2016, No.1, P.1-5.
