ПРОГРАММНЫЙ КОМПЛЕКС МОДЕЛИРОВАНИЯ ДИНАМИКИ МЕХАНИЗМОВ ЦИКЛИЧЕСКОЙ АВТОМАТИКИ
ПРОГРАММНЫЙ КОМПЛЕКС МОДЕЛИРОВАНИЯ ДИНАМИКИ МЕХАНИЗМОВ ЦИКЛИЧЕСКОЙ АВТОМАТИКИ
Научная статья
Кузин С.И.1, *, Никольский В.В.2, *
1, 2 ФГБОУ ВО Тульский государственный университет, Тула, Россия
* Корреспондирующий автор (godslav[at]yandex.ru; nvv.nb[at]mail.ru)
АннотацияИзделия современной техники, в состав которых входят механизмы и механические подсистемы циклической автоматики, представляют собой сложные технические объекты. Эффективная разработка таких объектов в условиях жесткой конкуренции (сжатые сроки, высокие требуемые характеристики, необходимость минимизации материальных затрат на проектирование и отладку) невозможна без использования автоматизации проектирования.
Проблема построения математических моделей проектируемых изделий и их подсистем является центральной при реализации САПР, поскольку успешность результатов проектирования зависит в первую очередь от качества моделей.
В статье рассмотрен программный комплекс моделирования динамики механизмов циклической автоматики с использованием программных средств в пакете программ SolidWorks и последующим анализе динамики как отдельных узлов, так и всех системы целиком в программной среде MatLab.
Ключевые слова: SolidWorks, MatLab, механические системы с неудерживающими связями, динамика механизмов циклической автоматики, математическое моделирование.
SOFTWARE PACKAGE FOR MODELING DYNAMICS OF CYCLIC AUTOMATION MECHANISMS
Research article
Kuzin S.I.1, *, Nikolsky V.V.2, *
1, 2 FSBEI of HE, Tula State University, Russia, Tula
* Corresponding author (godslav[at]yandex.ru; nvv.nb[at]mail.ru)
AbstractProducts of modern technology, which include mechanisms and mechanical subsystems of cyclic automation, are complex technical objects. Effective development of such objects under the conditions of fierce competition (tight deadlines, high characteristics required, the need to minimize material costs for design and debugging) is impossible without the use of design automation.
The problem of constructing mathematical models of designed products and their subsystems is central to the implementation of CAD since the success of design results depends primarily on the quality of the models.
The article discusses the software package for modeling the dynamics of cyclic automation mechanisms using the software in the SolidWorks software package and the subsequent analysis of the dynamics of both individual nodes and the entire system in the MatLab software environment.
Keywords: SolidWorks, MatLab, mechanical systems with non-holding connections, dynamics of cyclic automation mechanisms, mathematical modeling.
Как известно, облик нового изделия в основном определяется решениями, принимаемыми на ранних этапах проектирования. Поэтому разработка теоретических основ и методов математического моделирования для этих этапов является актуальной задачей.
К основным требованиям, предъявляемым к моделям, следует отнести адекватность и простоту. Рациональное сочетание этих свойств для конкретной модели обусловливается, по крайней мере, следующими факторами:
– особенностями проектируемых объектов;
– особенностями этапа проектирования, для которого предназначена математическая модель;
– производительностью, имеющейся в наличии вычислительной техники.
Удерживающие связи дают возможность звеньям механизмов циклической автоматики опираться друг на друга различными поверхностями в зависимости от нагрузки и состояния системы. Различные варианты опирания тел механической системы могут давать в итоге существенно отличающиеся значения обобщенных сил трения. Количество вариантов расчетных схем может быть очень велико, что для достаточно сложной механической системы приводит практически к невозможности априорного определения реализующейся при данной нагрузке расчетной схемы. Между тем, традиционные формы записи уравнений динамики механических систем с сухим трением либо вовсе не учитывают такую возможность, либо позволяют учитывать лишь несколько вариантов опирания, требуя при этом введения в математическое описание некоторых дополнительных соотношений. Указанные особенности привели к необходимости обоснования и разработки машиноориентированных способов математического описания механических систем с сухим трением, учитывающих все возможные расчетные схемы и позволяющих на основе некоторых критериев определять реализующееся в данный момент при данных условиях движение механической системы.
Наличие неудерживающих связей приводит к возможности изменения числа степеней свободы механической системы в процессе ее движения. По сравнению с механическими системами, стесненными только удерживающими связями, эта особенность значительно усложняет составление математического описания и анализ динамики. Для упрощения процесса математического моделирования было разработано математическое описание динамики механических систем, исключающее необходимость отдельного рассмотрения движения системы при нахождении ее точек на связях и отдельного – при оставлении ими связей. Моменты времени, соответствующие ослаблению или напряжению связи, определяются автоматически в процессе счета на вычислительной технике. При этом изменение количества степеней свободы механической системы не вызывают изменения количества и структуры дифференциальных уравнений предлагаемого математического описания.
Математическое описание динамики механизмов циклической автоматики, учитывающее все особенности их функционирования, изложена в работах [1], [2]. Разработанный метод моделирования, который в статье [3] назван методом систем неудерживающих связей, позволяет формировать математическое описание механизма автоматики конкретного механизма циклической автоматики в целом из математических описаний его типовых элементов (кинематических пар, звеньев, задаваемых сил).
Программно метод реализован средствами пакета MatLab [1]. Существенной проблемой, возникающей при использовании программной реализации метода, является необходимость ввода большого количества исходных данных связанных, в частности, с геометрическими характеристиками поверхностей, по которым могут происходить взаимодействия звеньев, инерционные характеристики звеньев.
Современное проектирование характеризуется широким использованием CAD программ, на основе которых разрабатывается 3D модель разрабатываемого образца циклической автоматики. 3D модель содержит все необходимые для динамических расчетов геометрические характеристики поверхностей и инерционные характеристики деталей. В связи с этим целесообразно было бы найти способ перенесения указанных данных из твердотельной модели в качестве исходных в программу MatLab, предназначенную для расчетов динамики.
В основе методов передачи данных в программу математического моделирования динамики механизмов циклической автоматики с сухим трением, предлагаемых в данной статье, лежит использование программных средств, основанных на 3D моделировании механизмов циклической автоматики в пакете программ SolidWorks и последующем анализе динамики как отдельных узлов, так и всех системы целиком в программной среде MatLab благодаря включённой в его состав графической среде имитационного моделирования Simulink/SimMechanics.
В основу рассматриваемого программного комплекса моделирования динамики механизмов циклической автоматики положены возможности трансляции 3D-модели из CAD-системы (SolidWorks) в среду MatLab.
Программа Simulink является приложением к пакету MatLab. Simulink является достаточно самостоятельным инструментом MatLab и при работе с ним совсем не требуется знать сам MatLab и остальные его приложения. С другой стороны, доступ к функциям MatLab и другим его инструментам остается открытым и их можно использовать в Simulink. Часть входящих в состав пакетов имеет инструменты, встраиваемые в Simulink (например, LTI-Viewer приложения Control System Toolbox – пакета для разработки систем управления).
При работе с Simulink пользователь имеет возможность модернизировать библиотечные блоки, создавать свои собственные, а также составлять новые библиотеки блоков. Преимущество Simulink заключается также в том, что он позволяет пополнять библиотеки блоков с помощью подпрограмм написанных как на языке MATLAB, так и на языках С++, Fortran и Ada.
При моделировании с использованием Simulink реализуется принцип визуального программирования, в соответствии с которым, пользователь на экране из библиотеки стандартных блоков создает модель устройства и осуществляет расчеты. При этом, в отличие от классических способов моделирования, пользователю не нужно досконально изучать язык программирования и численные методы математики, а достаточно общих знаний, требующихся при работе на компьютере и, естественно, знаний той предметной области в которой он работает.
При моделировании пользователь может выбирать метод решения дифференциальных уравнений, а также способ изменения модельного времени (с фиксированным или переменным шагом). В ходе моделирования имеется возможность следить за процессами, происходящими в системе. Для этого используются специальные устройства наблюдения, входящие в состав библиотеки Simulink. Результаты моделирования могут быть представлены в виде графиков или таблиц.
Рассмотрим последовательность действий при исследовании образца циклической автоматики в среде MatLab с использованием Simulink.
Сначала стоится 3D-модель исследуемого механизма в SolidWorks (рисунок 1).
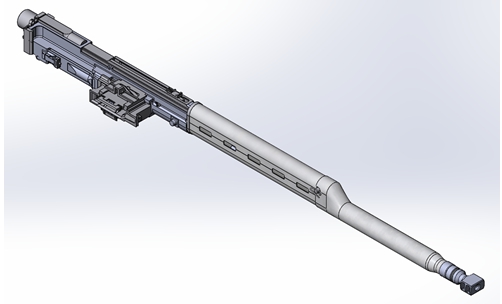
Рис. 1 – Внешний вид 3D модели механизма пулемёта в SolidWorks
Вторым шагом является исключение из модели деталей, не участвующих в исследуемом процессе, которые могут увеличить время при проведении расчётов по исследуемой модели (рисунок 2).
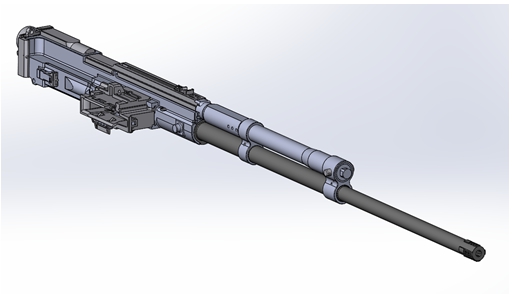
Рис. 2 – Внешний вид 3D модели механизма пулемёта в SolidWorks после исключения элементов, не участвующих в исследовании
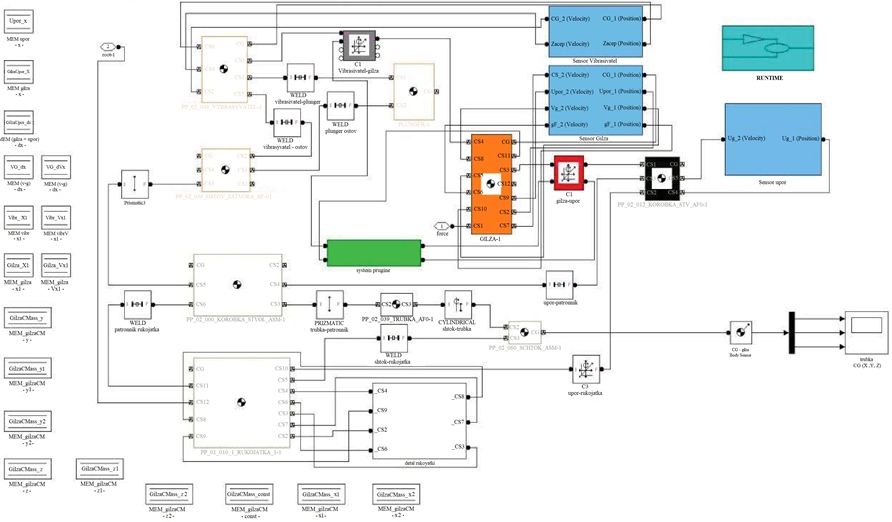
После подготовки модель преобразуется в xml файл и обрабатывается в среде MatLab с использованием Simulink. После исправления всех возможных ошибок, возникших при импорте xml файла. Строится схема модели механизма циклической автоматики в среде MatLab в соответствии с характером решаемой задачи (рисунок 3).
Рис. 3 – Пример схемы модели исследуемого механизма циклической автоматики в среде MatLab
После этого шага из исследуемой модели можно извлекать любые интересующие исследователя данные: приложенные сила к любой детали или узлу, а также перемещение или скорости деталей (рисунок 4).
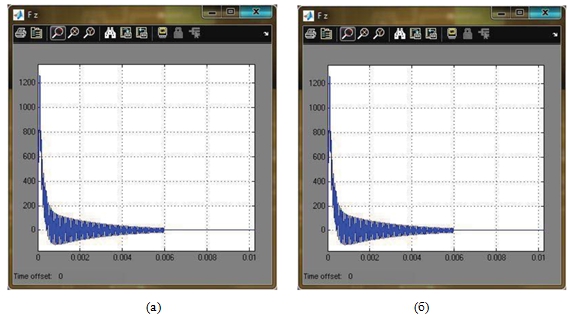
Рис. 4 – Пример выводимых данных исследуемой модели в среде MatLab;
а – график приложенной силы, б ‑ графики перемещений исследуемого звена
Рассмотренный программный комплекс моделирования динамики механизмов циклической автоматики позволяет выполнить наиболее полный и более точный анализ динамики механизмов с использованием унифицированной модели в среде MatLab, уточненной и параметризируемой непосредственно из CAD-системы разработки, что однозначно облегчает задачу математического описания исследуемых МС, проведения необходимых расчётов и позволяет оптимизировать процесс разработки новейших систем циклической автоматики.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- НикольскийВ.В. Математическое моделирование динамики механизмов и механических подсистем циклической автоматики / Никольский В. В. Тула: ТулГУ, 2008. 260 с.
- Математические модели пневмогидроэлектромеханических систем автоматического управления/Ю.Б.Подчуфаров, Г. Б. Кирик, В. В. Никольский, А. П. Матвеев, И. А. Владимиров. НТЦ «Информтехника», 1992, 272 с.
- Никольский В.В. О некоторых общих формах уравнений движения систем с трением / Никольский В.В., Смирнов Ю. П. // Известия ТулГУ. Естественные науки. 2014. Вып. С. 103–115.
- Подчуфаров Б.М. Динамика циклической автоматики / Подчуфаров Б.М. // Изв. вузов. Машиностроение. – 1961. № 8 – C. 14-22.
- Подчуфаров Б.М. Динамика циклической автоматики машины, имеющей подвижное основание / Подчуфаров Б.М. // Изд. вузов. Машиностроение. – 1963. № 6 – C. 84-94.
- Подчуфаров Б.М. Динамика автоматического оружия при стрельбе очередью / Подчуфаров Б.М. – 1971. – 111 с.
- Суслов Г.К. Теоретическая механика / Суслов Г.К. – М.; Л.: Гос. изд-во тех.-теор. лит., 1944. – 656 с.
- Кильчевский Г.К. Курс теоретической механики. В 2 т / Кильчевский Г.К. – М.: Наука, 1977.
- Вязгин В.А. О методе последовательного анализа вариантов для решения задач проектирования динамических систем / Вязгин В.А. // Изв. АН СССР. – 1985. – № 2. – С. 31-36.
- Бидерман В.Л. Прикладная теория механических колебаний / Бидерман В.Л. – М.: Высшая школа, 1972. – 416 с.
Список литературы на английском языке / References in English
- Nikolskyi V.V. Matematicheskoe modelirovanie dinamiki mexanizmov i mexanicheskix podsistem ciklicheskoy avtomatiki [Mathematical modeling of dynamics of mechanisms and mechanical subsystems of cyclic automation]/ V.V. Nikolskyi/ Tula / TulGu [Tula State University] -2008 – P 260 .[in Russian]
- Matematicheskoe modelirovanie pnevmogidrodinamicheskix system avtomaticheskogo upravleniya [Mathematical models of pneumatic hydroelectromechanical automatic control systems]/ U.B. Podchyfarov, G.B. Kiric, Nikolskyi V.V. et al. / NTC «Informtecnika» - 1992– P 272. [in Russian]
- Nikolskyi V.V. O necotoryx obchix formax uravneniy dvigeniya system c treniem [On some general forms of equations of motion for systems with friction] / Nikolskyi V.V., Smirnov U.P. // Izvestiya TulGu [Tula State University] Natural science. 2014 –No 3 – P 103-115. [in Russian]
- Podchyfarov U.B. Dinamica ciclicheskoy avtomatici [Dynamics of cyclic automation] / Podchyfarov U.B. // Engineering. – 1961 - № 8 – P 14-22 [in Russian].
- Podchyfarov U.B. Dinamica ciclicheskoy avtomatici mashiny, imeuchey podvignoe osnovanie. [Dynamics of cyclic automation of a machine with a movable base] / Podchyfarov U.B. Engineering. – 1963 - № 6 – P 84-94 [in Russian].
- Podchyfarov U.B. Dinamica avtomaticheskogo orygia pri strelbe ocheredyu. [Dynamics of automatic weapons when firing a burst] / Podchyfarov U.B. – 1971. – P 111 [in Russian].
- Syslov G.K. Teoreticheskaya mechanica [Theoretical mechanics] / Syslov G.K. Moscow- State publishing house. - 1944 – P 656. [in Russian].
- Kilchevskiy G.K. Kurs teoreticheskoy mechanici [The course of theoretical mechanics] / Kilchevskiy G.K. Moscow – Science. - 1977 [in Russian].
- Vyazgin V.A. O metode posledovatelnogo analysa variantov dlya recheniya zadach proectirovaniya dynamicheskix system [On the method of sequential analysis of options for solving dynamic system design problems] / Vyazgin V.A. Proceedings of the USSR Academy of Sciences. – 1985. - № 2. – P 31-36 [in Russian].
- Binderman V.L. Pricladnaya teoriya mexanicheskix kolebaniy [Applied theory of mechanical vibrations] / Binderman V.L. Moscow – Higher school. – 1972. – P. 416 [in Russian].