Проблема управляемого ядерного синтеза
Гарафутдинов А.А.
Проблема управляемого ядерного синтеза
Аннотация
Работа над проектом ядерного синтеза ведется во всем мире на протяжении около шестидесяти лет и до сих пор не завершена. Проблема состоит в том, что для осуществления реакции ядерного синтеза необходимо создать устройство, в котором в течение определенного времени необходимо удержать ядра легких атомов в определенной концентрации с энергией порядка 100 кэВ. Согласно критерию Лоусона для того, чтобы установка для ядерного синтеза была энергетически выгодна необходимо, чтобы произведение концентрации частиц на время ее удержания было не меньше определенного значения. Ввиду того, что высокотемпературная плазма крайне не устойчива, этот критерий не выполняется.
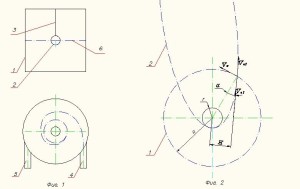
Предлагаю поразмыслить над другой схемой удержания высокоэнергетических частиц. Суть ее заключается в следующем. Внутрь вакуумной камеры поз.1 (см. Фиг.1) помещается (подвешивается) отрицательно заряженное ядро сферической формы (далее ядро) поз.2 с помощью проводника поз.3, который служит для удержания ядра в камере и для подведения и отведения заряда ядра. На некотором удалении от ядра под углом по направлению к ядру порядка 90 градусов из источника поз.4 вбрасываются предварительно ускоренные частицы одного из вида, участвующих в реакции с первоначальной скоростью, которая недостаточна для удержания ее на орбите поз.6 вокруг ядра. В обратном направлении из источника поз.5 вбрасываем частицы другого вида, участвующих в реакции, т. е. навстречу друг к другу. Поскольку скорости частиц не достаточны для центробежного удержания частиц на орбите, эти частицы под действием сил кулоновского притяжения начнут по спиралевидной орбите приближаться к ядру. Согласно закону сохранения момента количества движения скорости частиц по мере приближения к ядру будут увеличиваться. При достижения определенного радиуса, силы притяжения и центробежная уравновесятся, а орбита частиц будет близкой к круговой. Можно подобрать такие условия вбрасывания противоположно движущихся частиц, что орбиты их практически совпадут. В случае неупругого столкновения противоположно направленных частиц произойдет реакция их синтеза, что нам и нужно. В случае упругого столкновения частицы разлетятся в противоположные направления. Вот тут возникает очень важный вопрос, не потерям ли мы их. Предположим, для простоты, частицы, которые мы пытаемся столкнуть одинаковые (например, ядра атомов дейтерия). В этом случае, как следует из теории удара, при их столкновении они обменяются величинами своих скоростей, что не существенно. Но могут существенно изменяться их направления. Из физики мы знаем, что в поле кулоновских сил (так же как и гравитационных) частицы могут покинуть это поле в случае, когда кинетическая энергия частицы станет равной или превысит потенциальную энергию притяжения.
Условием же удержания частиц на стационарной круговой орбите является равенство силы притяжения и силы центробежной. Скорость удержания на круговой орбите в 1,41 раз меньше, чем скорость преодоления силы притяжения. В нашем случае после столкновения скорости частиц и расстояния до ядра сильно не изменились, следовательно, частицы не смогут оторваться от ядра. Но они поменяют свои орбиты. Так как направление векторов скоростей частиц после их столкновения могут быть произвольными, то орбиты частиц станут эллиптическими и повернут свою плоскость относительно первоначальной плоскости орбиты. У эллиптической орбиты есть две крайние точки: перигелий – точка максимального сближения с центром притяжения (центр ядра) и афелий – точка максимального удаления от центра притяжения. Для нас являются неприемлемыми орбиты, у которых расстояние от точки перигелия до центра притяжения будет меньше или равна радиусу поверхности ядра. Определим, при каких условиях это может произойти и какова вероятность потери частиц в результате их падения на ядро. Допустим, частица вращалась до столкновения с другой частицей вокруг ядра по круговой орбите поз. 1 со скоростью VZ (см. Фиг.2). После столкновения, рассматриваемая частица
изменит вектор скорости на Vе1 или Vе2, а орбита поз.2 станет эллиптической достигающей в перигелии поверхности ядра. Нужно заметить, что орбиты частиц со скоростями после столкновения Vе1 или Vе2, совпадают, поэтому дальнейшие рассуждения будем связывать со скоростью Vе1. По закону сохранения момента количества движения:
m∙Vе1∙H= m∙Vеп∙r , (1)
где m – масса частицы,
H – Плечо вектора скорости Vе1,
Vеп – скорость частицы в перигелии,
r – радиус ядра.
Так как
H=R∙sin α ,
α – угол между линией, связывающей центры ядра и частицы, и вектором Vе1.
Выражение (1) можно преобразовать к виду:
Vеп= Vе1∙(R⁄ r) ∙sin α. (2)
В соответствии с законом сохранения энергии сумма кинетической и потенциальной составляющих полной энергии частицы при движении ее в потенциальном поле остается неизменной:
½∙ m∙Vеп2- k∙(qQ⁄ r)= ½∙ m∙Vе12- k∙(qQ⁄ R) ,
где k = 1/(4πε0) – коэффициент пропорциональности, ε0 = 8,85∙10-12Ф/м – электрическая постоянная,
q – электрический заряд частицы,
Q – электрический заряд ядра,
После преобразования и с учетом (2):
½∙ m∙Vе12[R2⁄ r2∙sin2α-1]= k∙qQ[1⁄r-1⁄R] (3)
Скорость найдем из условия удержания частицы на круговой орбите:
m∙VZ 2⁄ R =k∙(qQ⁄ R2)
Из вышеизложенных рассуждений
VZ ≈ Vе1
И отсюда
m∙Vе12 ≈ m∙VZ 2 =k∙(qQ⁄ R)
Вставим полученное выражение в формулу (3) и после преобразования получим:
sin α=(r/R)∙[(2R-r)⁄r]½
Из анализа последней формулы можно сделать вывод, что чем меньше соотношение r/R тем меньше угол α, а, следовательно, и потери частиц из-за падения их на ядро. Следовательно, для уменьшения потерь частиц необходимо, чтобы радиус ядра был как можно меньше. Но с другой стороны, чтобы вокруг ядра удержать наибольшее число частиц, заряд ядра необходимо обеспечить наибольшим, так как суммарный заряд всех удерживаемых ядром частиц, не может превышать по величине заряд самого ядра. Отсюда следует, что ядро должно иметь максимальную плотность заряда.
Чтобы при падении частиц на ядро они не терялись без пользы, ядро можно покрыть слоем материала при попадании, на который будут выбиваться другие полезные заряженные частицы, которые будут участвовать в синтезе или просто произойдет ядерная реакция.
Для того, чтобы уменьшить потери от падения частиц на ядро можно применить другой способ подачи частиц в камеру. Заключается он в том, чтобы сначала подавать частицы одного вида. Собираясь на близких орбитах и двигаясь в одном направлении частицы за счет магнитных полей, возникающих благодаря их движению, притягиваются друг, к другу образуя плотный торообразный жгут. Затем начинают подавать частицы в обратном направлении. Преимуществом такого способа представляется то, что при «обстреле» плотного жгута вероятность неупругого столкновения частиц повышается и уменьшается вероятность падения частиц на ядро. Затем подаем в камеру частицы, поданные в первый раз, а затем подаем частицы в обратном направлении и так далее.
Предложенная схема удержания высокоэнергетических частиц позволяет управлять процессом реакции синтеза, как подачей частиц, так и за счет изменения заряда ядра (с уменьшением по величине заряда ядра радиус орбит частиц увеличивается и, следовательно, изменяется их концентрация и наоборот). Если величина заряда будет колебаться, то орбиты частиц начнут также изменяться, что приведет к пересечению орбит разнонаправленных частиц и таким образом увеличит вероятность их взаимного столкновения. Кроме того, эллиптические орбиты частиц из-за релятивистского изменения массы частиц в процессе их движении по орбите будут прецессировать, то есть их орбиты будут поворачиваться в сторону вращения частиц. Этот эффект увеличивает вероятность пересечения орбит частиц.