ПОСТРОЕНИЕ РАСПРЕДЕЛЕННОГО АЛГОРИТМА ПОИСКА СТРУКТУРНЫХ РАЗЛИЧИЙ В КАТЕГОРИЯХ ИЗОМОРФИЗМА
Воробьева М.С.1, Воробьев А.М.2, Егоров Ю.А.3
1Кандидат технических наук, доцент, 2Аспирант, 2Магистрант, Тюменский государственный университет
ПОСТРОЕНИЕ РАСПРЕДЕЛЕННОГО АЛГОРИТМА ПОИСКА СТРУКТУРНЫХ РАЗЛИЧИЙ В КАТЕГОРИЯХ ИЗОМОРФИЗМА
Аннотация
Цель работы: разработать распределенный алгоритм для решения задачи поиска структурных различий в графах с точки зрения изоморфиза, показать применение алгоритма на примере поиска структурных различий в web-графах. В результате сформулирована задача поиска различий в графах, описан алгоритм поиска структурных различий и проведен эксперимент, подтверждающий, что структуры ресурсов имеют значение для продвижения.
Ключевые слова: Изоморфизм подграфов, сравнение графов, объекты сложной структуры, поиск структурных различий, web-графы
Vorobyova M.S. 1, Vorobyov A.M.2, Egorov Yu.A.3
1PhD in Engineering, Associate Professor, 2Postgraduate student, 3Master's degree student,
Tyumen State University
CONSTRUCTION OF DISTRIBUTED ALGORITHM FOR SEARCH FOR STRUCTURAL DIFFERENCES IN ISOMORPHISM CATEGORIES
Abstract
The main goal of this work is to develop a distributed algorithm for solution of the problem of search for structural differences in graphs from the point of view of isomorphism, and to show the application of the algorithm on the example of search for structural differences in web-graphs. The problem of search for differences in graphs is formulated as a result, the algorithm for structural differences searching is described as well, and finally the experiment was conducted, confirming the resource structures are important for progression.
Keywords: Isomorphism of subgraphs, comparison of graphs, objects of complex structure, search for structural differences, web-graphs
По различным оценкам основная доля сети Интернет – 60-90% – приходит на интернет-ресурсы через поисковые системы, такие как Google, Яндекс и Baidu. С ростом конкуренции на интернет-площадках поисковые системы с каждым годом ужесточают требования к интернет-ресурсам: поисковые системы отслеживают тысячи факторов, на основании которых формируется поисковая выдача. Постоянная разработка и внедрение новых алгоритмов ранжирования обязывают владельцев интернет-ресурсов уделять особое внимание множеству факторов ранжирования.
Кроме того, в современных алгоритмах ранжирования наиболее простые для манипуляции факторы стали менее весомы для поисковых роботов, и изменение их теперь уже не столь значимо отражается на позициях сайта. Например, если раньше для попадания сайта на первое место достаточно было иметь большую ссылочную массу (количество ссылающихся внешний ресурсов на сайт), превышающую конкурентов, то сейчас значимость этого фактора сильно занижена в силу появления различных инструментов воздействия на этот фактор и, как следствие, выведение в лидирующие позиции сайтов, которые могут не в полной мере отвечать запросам пользователей.
Если рассмотреть каждый отдельный сайт в виде графа, где вершиной графа является страница интернет-сайта, а ребром – ссылка на страницу, то при сравнении эталонного интернет-ресурса и продвигаемого сайта можно определить параметры и их значения, необходимые для достижения желаемых результатов.
Пусть даны объекты сложной структуры S и T, где каждый объект представляет собой граф ![]() , где
, где ![]() – множество вершин,
– множество вершин, ![]() – множество ребер графа. Каждая вершина
– множество ребер графа. Каждая вершина ![]() является HTML-страницей и имеет кортеж признаков
является HTML-страницей и имеет кортеж признаков ![]() , где
, где ![]() – характеристика HTML-страницы.
– характеристика HTML-страницы. ![]() – множество ребер графа, где
– множество ребер графа, где ![]() – это функция перехода от страницы u к странице v.
– это функция перехода от страницы u к странице v.
Необходимо провести сравнение графов S и T и найти граф ![]() такой, что:
такой, что:
1) ![]() – множество вершин графа S, соответствующих условиям:
– множество вершин графа S, соответствующих условиям:
- Вершина
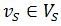 не имеет соответствующей вершины в графе T;
не имеет соответствующей вершины в графе T; - Вершина
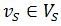 имеет различные значения соответствующих признаков
имеет различные значения соответствующих признаков 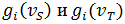 с соответствующей вершиной
с соответствующей вершиной 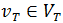 ;
;
2) ![]() – множество ребер графа S, не имеющих соответствующих ребер в графе T.
– множество ребер графа S, не имеющих соответствующих ребер в графе T.
Для сравнения структур графов S и T решается задача изоморфизма графов – поиск взаимнооднозначного соответствия между вершинами двух графов. Для решения разработан распределенный алгоритм поиска структурных различий, в основу которого легли подходы и методы, описанные в работах [1], [3], [4]. Входными данными являются графы ![]() представленных с помощью матриц достижимости
представленных с помощью матриц достижимости ![]() . Выходными –множество всех матриц перестановок для графов S и T, где каждая матрица перестановок представляет собой биекцию между вершинами графов. Асимптотическая сложность составляет
. Выходными –множество всех матриц перестановок для графов S и T, где каждая матрица перестановок представляет собой биекцию между вершинами графов. Асимптотическая сложность составляет ![]() , где N – количество вершин в графе S, M – количество вершин в графе T.
, где N – количество вершин в графе S, M – количество вершин в графе T.
Алгоритм был разработан для модели акторов и включает в себя:
- управляющий актор, порождающий конечное количество вычислительных акторов и управляющий списком заданий;
- вычислительные акторы могут отправлять управляющему актору новые задания и запрашивать задания на выполнение
- актор вывода, осуществляющий формирование и обработку конечного результата.
Задание, которое выполняется вычислительным актором, представляет собой кортеж из двух элементов:
- промежуточная матрица перестановок P, которая потенциально может быть искомой матрицей перестановок, удовлетворяющей условию
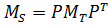 ;
; - K – номер строки матрицы P, которую необходимо заполнить.
Управляющий актор инициализирует решение задачи, управляет списком заданий и пулом акторов, завершает решение задачи.
Инициализация осуществляется с помощью функции start(M1,M2,Workers_count), где M1 – матрица смежности графа S, M2 – матрица смежности графа T, Workers_count – количество потоков, которые необходимы для решения задачи. Данная функция осуществляет создание первого задания {P,0}, где P – матрица перестановок, регистрацию глобального имени актора (server), создание вычислительных акторов.
Функция loop(Workers,Tasks,Workers_count) получает и обрабатывает сообщения, где Workers – список вычислительных акторов, запросивших новое задание, Tasks – список заданий, ожидающих выполнения, Workers_count – количество вычислительных акторов. Форматы сообщений, которые принимает актор и вызовы функций, осуществляются при получении сообщений (Таблица 1).
Таблица 1 - Сообщения, принимаемые управляющим актором
| Формат сообщения | Описание |
| {take_task, Wpid} | Запрос от вычислительного актора на получение задания, где Wpid – адрес, по которому нужно отправить задание. Вызывает функцию send_task, после – функцию loop |
| {new_task, Newp, K} | Запрос от вычислительного актора на добавление задания в список, где Newp – одна из матриц перестановок для обработки, K – строка Newp для заполнения. Вызывает функцию add_task, после – функцию loop |
Выдачу заданий вычислительным акторам осуществляет функция send_task(Workers,Tasks,Wpid,Workers_count), где Workers – список акторов, ожидающих новое задание; Tasks – список заданий; Wpid – адрес, по которому нужно отправить новое задание; Workers_count – общее количество вычислительных потоков. Данная функция выбирает одно из трех поведений в зависимости от входных данных:
- если список заданий, ожидающих обработку, пуст, управляющий актор добавляет вычислительный актор в список ожидающих новое задание;
- если список заданий, ожидающих обработку, пуст, и все вычислительные акторы ожидают нового задания, значит, все задания выполнены, и управляющий актор вызывает функцию завершения решения;
- если список заданий не пуст, первое задание из списка заданий отправляется запросившему актору.
Функция send_task возвращает Nworkers – новый список акторов, ожидающих новое задание и Ntasks – новый список заданий.
Функция add_task(Workers,Tasks,P,K), где Workers – список акторов, ожидающих новое задание; Tasks – список заданий; P – матрица перестановок, полученная от вычислительного актора; K – номер строки матрицы P, который необходимо заполнить, добавляет задания в очередь и реализует одно из двух поведений в зависимости от входных данных:
- если список акторов, ожидающих задание не пуст, новое задание разу же отправляется первому актору из списка, минуя список заданий;
- если список акторов, ожидающих задание пуст, новое задание записывается в начало списка заданий.
Функция возвращает Nworkers – новый список акторов, ожидающих новое задание; Ntasks – новый список заданий.
Терминарция работы алгоритма осуществляется с функцией close(Workers), где Workers – список акторов, ожидающих новое задание, выполняя которую, актор отправляет всем ожидающим акторам сообщение о том, что задача решена и завершает работу управляющего актора.
Вычислительный актор, выполняющий поиск матриц перестановок, осуществляет следующие функции: инициализации, получения задания, поиска матрицы перестановок.
Функция инициализации start(M1,M2) получает исходные данные и вызывает функцию take_task, где M1 – матрица смежности графа S, M2 – матрица смежности графа T.
Функция получения задания take_task(M1,M2) (M1 – матрица смежности графа S, M2 – матрица смежности графа T) отправляет управляющему актору запрос на получение нового задания и ожидает ответа. Дальнейшее поведение, которое выбирает актор, зависит от ответа управляющего актора. Форматы сообщений и поведение при их обработке представлены в таблице 2.
Таблица 2 - Сообщения, принимаемые вычислительным актором
| Формат сообщения | Описание |
| {run, {P, K}} | Ответ от управляющего актора, инициализирующий выполнение нового задания, где P – матрица перестановок, K – строка матрицы перестановок для заполнения. Вызывает функцию backtrack |
| {close} | Ответ от управляющего актора, сигнализирующий о том, что задача решена. Вызывает функцию exit, завершающую работу актора |
Функция поиска матрицы перестановок backtrack(M1,M2,P,K) выполняет следующие этапы:
a. если K>m, то P - искомая матрица перестановок, актор отправляет актору вывода полученный результат и запрашивает у управляющего актора новое задание;
b. иначе, для каждого ![]() выполняем следующее:
выполняем следующее:
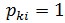 , остальные элементы i-й строки равны 0;
, остальные элементы i-й строки равны 0;- если выполняется условие
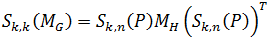 , то актор отправляет управляющему актору новое задание, содержащее полученную матрицу и K +1 – номер следующей строки, которую необходимо заполнить;
, то актор отправляет управляющему актору новое задание, содержащее полученную матрицу и K +1 – номер следующей строки, которую необходимо заполнить;
Параметрами функции являются: матрица смежности M1 графа S, матрица смежности M2 графа T, промежуточная матрица перестановок P, K – номер строки, которую необходимо заполнить в матрице P. Актор вывода получает найденные матрицы перестановок от вычислительных акторов и осуществляет их сохранение в массив и вывод результата.
В результате тестирования работы алгоритма поиска структурных различий было выявлено три типа результатов сравнения двух графов.
Результат 1 типа: Алгоритм вернул одну матрицу перестановок (рис.1). Между вершинами графов S и T существует единственное взаимнооднозначное соответствие: объекты имеют одинаковую структуру, значит, первый уровень соответствия выполнен, и сравнивать необходимо внутренние характеристики каждого ребра и вершины графа, т.е. показатели конкретных страниц и ссылок между страницами сайта.
Результат 2 типа: Алгоритм вернул несколько матриц перестановок (рис.2). В данном случае из нескольких матриц перестановок нужно выбрать одну, наиболее релевантную исследуемому графу. Для того чтобы правильно определить релевантную структуру, для каждой вершины задается параметр ![]() , который позволяет однозначно сопоставить вершины графов S и T. Как только всем вершинам находится однозначное соответствие, можно утверждать, что найдена матрица перестановок P, противном случае, если не удается найти матрицу P, переходим к случаю 3.
, который позволяет однозначно сопоставить вершины графов S и T. Как только всем вершинам находится однозначное соответствие, можно утверждать, что найдена матрица перестановок P, противном случае, если не удается найти матрицу P, переходим к случаю 3.
Результат 3 типа: Матрица перестановок не найдена (рис.3). В этом случае, для соответствующей вершины с параметрами ![]() исследуемого графа T применяются функция
исследуемого графа T применяются функция ![]() или функция
или функция ![]() , которые представляют собой объединение, добавление, удаления соответствующей вершины графа, таким образом, чтобы привести структуру исследуемого графа T к виду эталонного графа S.
, которые представляют собой объединение, добавление, удаления соответствующей вершины графа, таким образом, чтобы привести структуру исследуемого графа T к виду эталонного графа S.
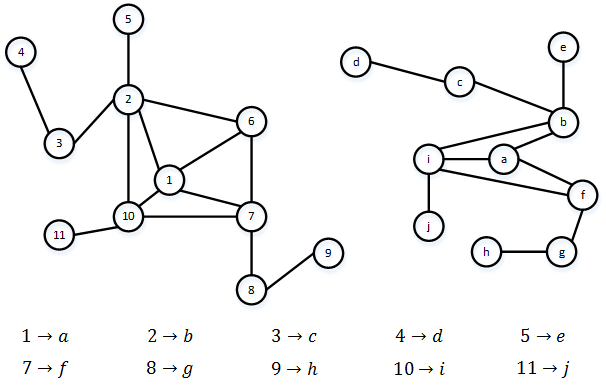
Рис. 1 - Результат работы алгоритма (1 тип)
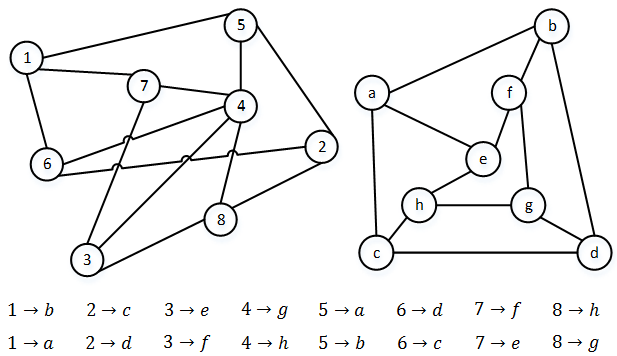
Рис. 2 - Результат работы алгоритма (2 тип)
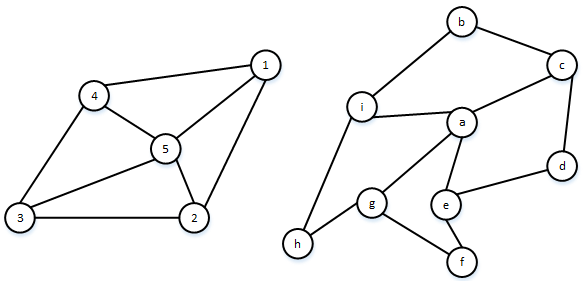
Рис. 3 - Результат работы алгоритма (3 тип)
Для реализации алгоритма поиска структурных различий разработано приложение на языке Erlang. В качестве данных для эксперимента использованы данные интернет-ресурсов, связность которых не контролировалась. Уровень вложенности доменов исследуемых сайтов варьировался от 2 до 4, количество страниц, исходя из предоставленной карты сайта, составляло не более 1000.
Для анализа подбиралось случайное ключевое слово, по которому проходил отбор сайта, находящегося на первой позиции в поисковых системах Яндекс и Google и рассматривался как эталон. Эксперимент проводился с целью проверки, является ли параметр «структура интернет-сайта» необходимым при ранжировании в поисковой системе.
В ходе эксперимента были отобраны интернет-ресурсы по тематике «получение дополнительного высшего образования в регионе», занимающие лидирующие позиции в поисковых системах Яндекс и Google. Для блока высокочастотных фраз, по которым пользователи находят данные услуги, найдены 15 фраз, по каждой из которых в поисковых системах есть сайт, который располагается на первой строчке поиска, принятый за эталон.
По каждой фразе из заданного блока были взяты интернет-сайты, не попавшие в выдачу поисковиков на первое место. Каждый из таких сайтов и являлся исследуемым. Таким образом, каждый исследуемый сайт сравнивался с эталонным по ключевому запросу, и каждое сравнение было отнесено к одному из типов нахождения изоморфизма.
По данной тематике было проведено 135 сравнений, из которых 25 дали результат первого типа, 34 – результат второго типа и 76 – результат третьего типа. Причем 80% изоморфизмам по 1 типу было определено в первых трех строчках выдачи, что подтверждает гипотезу о факторе ранжирования по структуре.
Список литературы / References
- Воробьев, А. М. Интеллектуальный анализ и кластеризация WEB данных / А. М. Воробьев // Математическое и информационное моделирование: сборник научных трудов. - Тюмень: Издательство ТюмГУ – 2014. – №14. – 313 с.
- Егоров, Ю. А. Модификация алгоритма Ульмана для многопроцессорных систем / Ю. А. Егоров // Материалы XVII Всероссийской конференции молодых ученых по математическому моделированию и информационным технологиям. – 2016. – С. 86-87.
- Ullmann J. R. An Algorithm for Subgraph Isomorphism Problem /J. R. Ulmann. – Journal of the Association for Computing Machinery. – 1976. – VoI 23(1). – P. 31-42.
- Cordella L.P. A (sub)graph isomorphism algorithm for matching large graphs / L.P. Cordella, P. Foggia, C. Sansone // IEEE Transactions on Pattern Analysis and Machine Intelligence. – 2004. – vol. 26. – P. 1367-1372.
Список литературы на английском языке / References in English
- Vorobjoev, A. M. Intellektual'nyj analiz i klasterizacija WEB dannyh [Web data clustering and data mining] / A. M. Vorobjev // Matematicheskoe i informacionnoe modelirovanie: sbornik nauchnyh trudov [Math and information modeling: scientific papers collection]. – Tyumen: Izdatelstvo TGU - 2014. – Vol. 14. – 313 p. [in Russian].
- Egorov, Ju. A. Modifikacija algoritma Ul'mana dlja mnogoprocessornyh sistem [Ullmann algorithm improvement for multiprocessor systems] / Ju. A. Egorov // Materialy XVII Vserossijskoj konferencii molodyh uchenyh po matematicheskomu modelirovaniju i informacionnym tehnologijam [Materials of the XVII all-Russian conference of young scientists on mathematical modeling and information technologies]. – 2016. – P. 86-87. [in Russian].
- Ullmann J. R. An Algorithm for Subgraph Isomorphism Problem /J. R. Ulmann. – Journal of the Association for Computing Machinery. – 1976. – VoI 23(1). – P. 31-42.
- Cordella L.P. A (sub)graph isomorphism algorithm for matching large graphs / L.P. Cordella, P. Foggia, C. Sansone // IEEE Transactions on Pattern Analysis and Machine Intelligence. – 2004. – vol. 26. – P. 1367-1372.
