ОЦЕНКА ВРЕМЕНИ МОДЕЛИРОВАНИЯ СИСТЕМЫ НА ОСНОВЕ ТАБЛИЦ СОБЫТИЙ В РАМКАХ ЭКСПЕРИМЕНТАЛЬНОГО ОПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ СОБЫТИЙ
Кулешова О.Н.
ORCID: 0000-0003-3745-7066, Аспирант, Севастопольский государственный университет
ОЦЕНКА ВРЕМЕНИ МОДЕЛИРОВАНИЯ СИСТЕМЫ НА ОСНОВЕ ТАБЛИЦ СОБЫТИЙ В РАМКАХ ЭКСПЕРИМЕНТАЛЬНОГО ОПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ СОБЫТИЙ
Аннотация
Рассматриваются способы оценки вероятности событий систем, специфицированных средствами языка таблиц событий. Описывается методика определения вероятностей событий. Производится расчет минимального числа прогонов модели для таблиц событий с различным числом условий. Проводится обзор методики расчета затрат времени для моделирования системы и рассчитываются временные затраты для моделирования в рамках эксперимента по определению вероятностей событий для систем, включающих таблицы событий различной сложности.
Ключевые слова: таблицы событий, вероятность событий, оценка времени моделирования.Kuleshova O.N.
ORCID: 0000-0003-3745-7066, Postgraduate student, Sevastopol State University
ASSESSMENT OF TIME FOR SYSTEM SIMULATION BASED ON EVENTS TABLES WITHIN THE EXPERIMENTAL DETERMINATION OF THE EVENTS PROBABILITY
Abstract
In the article is devoted to the review of methods for assessing the event probability of the system, specified by means of events table language. It describes the method of events probabilities determining. In the paper the author calculates the minimum runs number of the model for events tables with different number of conditions. The review of methods for calculating the time cost for the simulation system and the time required for a simulation as part of an experiment to determine the events probabilities for systems incorporating varying complexity event table.
Keywords: events tables, events probabilities, simulation time assessment.Важным этапов реализации современных событийных систем является моделирование их поведения. Для автоматизации процесса моделирования систем управления, разработанных средствами языка таблиц событий (ТС) [1], необходимы методы и средства генерации входных наборов событий.
Целью генерации входных наборов событий являются пакеты входных данных обеспечивающих в процессе моделирования покрытие всех таблиц событий системы, поиск минимального пути в системе, создание наиболее или наименее вероятных ситуаций, достижения выполнения определённых действий.
Для организации процесса генерации входных наборов данных ориентированных на наиболее или наименее вероятные ситуации необходимы данные о вероятностях каждого события. Такие данные могут быть получены следующими способами: экспертная оценка вероятности каждого события, экспертная оценка вероятностей состояния условий, экспериментальная оценка вероятностей.
Экспертные оценки связаны с финансовыми (заработная плата проектировщиков и экспертов) и временными (время выполнения работы в человеко-часах) затратами.
Экспериментальная оценка требует затрат машинного времени. Финансовые затраты в этом случае можно оценить как затраченные на обеспечение электричеством, и потери от занятости оборудования на задачи моделирования.
Для определения наиболее доступного метода оценки вероятностей событий, актуальной задачей является начальная оценка времени эксперимента абстрактной системы с усреднёнными параметрами. В результате таких расчетов будут получены данные, на основе которых можно принимать решение о перспективности более точной оценки затрат машинного времени для конкретной системы.
Экспериментальное определение вероятностей событий связано с необходимостью проведения прогонов модели (системы ТС) в количестве достаточном для получения достоверных значений. Эксперимент требует затрат времени, а следовательно и финансов, чем больше прогонов модели, тем эти затраты выше. Средством достижения компромисса между максимумом информации и минимумом затрат ресурсов является план эксперимента [2]. Весь комплекс действий по планированию эксперимента разделяют на две самостоятельные функциональные части: стратегическое планирование и тактическое планирование. Стратегическое планирование включает разработку условий проведения эксперимента, определение режимов, для обеспечения наибольшей информативности эксперимента. Тактическое планирование должно обеспечивать достижение заданных точности и достоверности результатов.
С целью определения доступности экспериментального моделирования необходимо произвести расчеты затрат времени при усреднённых параметрах, таких как вычислительная мощность компьютера, размеры и количество таблиц событий в системе.
Формирование стратегического плана выполняется в так называемом факторном пространстве. Факторное пространство – это множество внешних и внутренних параметров, значения которых исследователь может контролировать в ходе подготовки и проведения эксперимента. Математические методы планирования экспериментов основаны на так называемом кибернетическом представлении процесса проведения эксперимента.
Факторами (входными переменными) являются: количество простых и сложных условий; количество простых и сложных действий; время определения состояния простого условия и сложного условий; время выполнения простого и сложного действий; количество таблиц событий в системе; число прогонов для достоверного определения вероятностей событий.
Выходные переменные в данном случае – это общее время моделирования для получения вероятностей событий с заданной точностью и вероятности событий.
Целью проведения эксперимента является определение вероятности каждого события в системе.
В качестве оценки вероятности P события ![]() (в терминах спецификации таблиц событий R) выступает частота его свершения:
(в терминах спецификации таблиц событий R) выступает частота его свершения:
![]() , где N - число реализаций модели; µ - число свершений данного события.
, где N - число реализаций модели; µ - число свершений данного события.
Использование частоты ![]() в качестве оценки искомой вероятности P основано на теореме Я. Бернулли, которую для конкретной задачи можно записать в формализованном виде:
в качестве оценки искомой вероятности P основано на теореме Я. Бернулли, которую для конкретной задачи можно записать в формализованном виде:
![]()
Точность и достоверность этой оценки связаны c определением достоверности:
![]()
Задача сводится к нахождению такого количества реализаций N, чтобы оценка отличалась от искомого значения ![]() менее, чем на с заданной достоверностью. Здесь ε – абсолютное значение, которое характеризует точность оценки.
менее, чем на с заданной достоверностью. Здесь ε – абсолютное значение, которое характеризует точность оценки.
Для нахождения функциональной связи между точностью, достоверностью и числом реализаций модели вводится переменная ![]() – результат исхода i-й реализации модели:
– результат исхода i-й реализации модели:
Тогда частота свершения события (оценка искомой вероятности) будет определяться следующим выражением:
![]()
Тогда частота свершения события (оценка искомой вероятности) будет определяться следующим выражением:
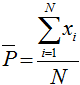
Величина ![]() - случайная и дискретная, имеющая при таком задании
- случайная и дискретная, имеющая при таком задании ![]() биномиальное распределение с характеристиками:
биномиальное распределение с характеристиками:
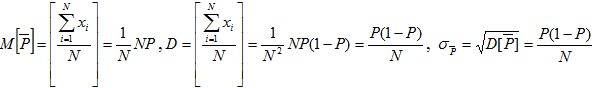
На основании теоремы Лапласа (частный случай центральной предельной теоремы), при больших значениях числа реализаций N биномиальное распределение достаточно хорошо согласуется с нормальным распределением [3].
Следовательно, можно записать:
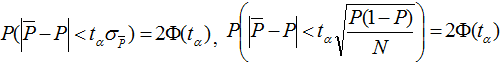
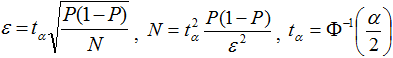 α – достоверность, tα – аргумент функции Лапласа
α – достоверность, tα – аргумент функции Лапласа
ε - абсолютное значение, ![]() , где σ количество десятичных знаков вероятности P равных «0» до знаков отличных от «0» плюс 2.
, где σ количество десятичных знаков вероятности P равных «0» до знаков отличных от «0» плюс 2.
Результаты расчетов необходимого числа прогонов при количестве условий от 2 до 10 приведены на рисунке 1.
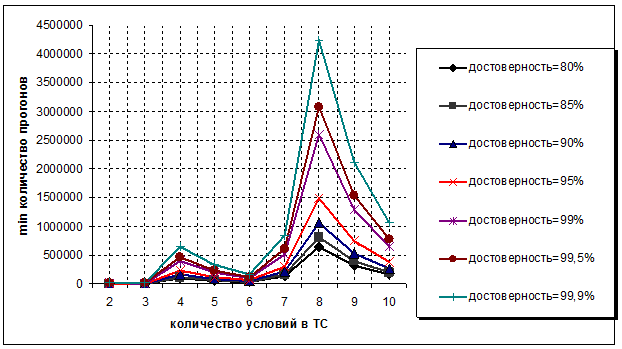
Рис. 1 - Зависимость число прогонов для достоверного определения вероятностей событий от количества условий ТС
В дальнейших исследованиях используется достоверность равная 80%.
Оценка времени эксперимента проводится по формуле:
![]()
Время моделирования системе равно сумме затрат времени на моделирование каждой ТС.
Для оценки времени моделирования таблицы событий используется формула:
![]()
где mEE – количество простых условий в ТС, tEE – время выполнения простого условия, mCE – количество сложных условий в ТС, tCE – время выполнения сложного условия, где kEA – количество простых действий в ТС (переходов), tEA – время выполнения простого действия, kCA – количество сложных действий в ТС (функций), tCA – время выполнения сложного действия.
Время выполнения условий и действий зависит от настроек СУБД PostgreSQL [4], с помощью которой реализована система и параметров ЭВМ, которая будет производить моделирование.
Оценочные вычисления проводятся, используя данные теста производительности PostgreSQL pgbench [5].
Формулу оценки времени моделирования ТС модифицируется, основываясь на транзакциях типа «read-only» и «read-write».
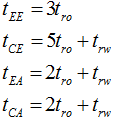
где ![]() – общее число условий в ТС,
– общее число условий в ТС, ![]() – общее число действий в ТС.
– общее число действий в ТС.
![]()
Для оценочных расчетов рассматриваются обобщающие варианты структур ТС.
По условиям:
- простая ТС (Easy) – все условия простые;
- средняя ТС (Medium) – 50% условий простые, 50% – сложные;
- сложная ТС (Large) – все условия сложные.
По действиям:
- простая ТС (Easy) – 1 выполняемое действие;
- средняя ТС (Medium) – 5 выполняемых действий;
- сложная ТС (Large) – 10 выполняемых действий.
Для заданных вариантов структур вводится параметр χ – процентное содержание сложных действий в таблице событий. Учитывая, что не все действия в ТС выполняются при каждом событии, заменим k – общее число действий, на kav – среднее число выполняемых при моделировании действий.
Преобразованная формула имеет вид:
![]()
На основании данных исследования [5], проводится оценка времени выполнения транзакции «read-only» и «read-write» для БД размером до 150 Мб при конфигурации оборудования HP DL380 G5 (2x Xeon E5450 3Ghz, 16GB DDR2 RAM), Intel S3700 100GB SSD, СУБД PostgreSQL 9.0 для 1 клиента:
read-only ≈ 10000 транзакций в секунду;
![]() ;
;
read-write ≈ 1000 транзакций в секунду;
![]() ;
;
Результаты расчетов времени моделирования 1 клиентом БД таблицы событий представлены на рисунке 2.
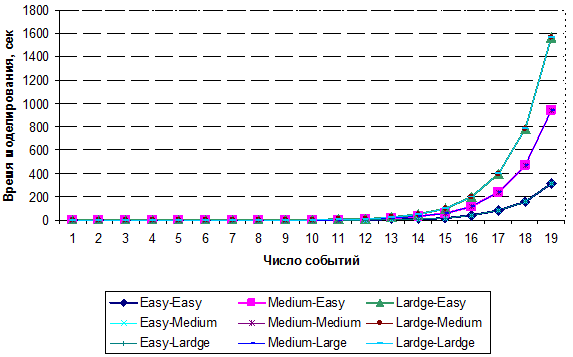
Рис. 2 – Зависимость времени моделирования ТС от числа условий
На основе полученных результатов, можно сделать вывод, что значительный рост времени моделирования происходит при числе условий больше 7.
Проводится расчет времени моделирования системы ТС, включающей таблицы событий с количеством условий от 2 до 10. Для обобщения вычислений, делается предположение, что количество таблиц с различным числом условий – равное. Так же, время моделирования ТС как принимается как среднее время. Результаты приведены на рисунке 3.
Проведя аналогичные расчеты для системы ТС, включающей таблицы событий с количеством условий от 2 до 6 были получены результаты, представленные на рисунке 4.
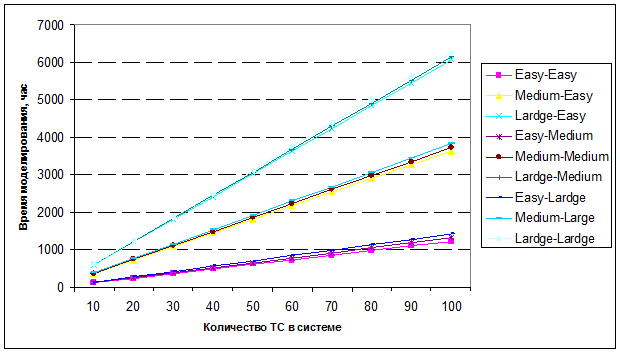
Рис. 3 – Зависимость времени моделирования системы ТС с таблицами, содержащими от 2 до 10 условий (моделирование 1 клиентом БД)
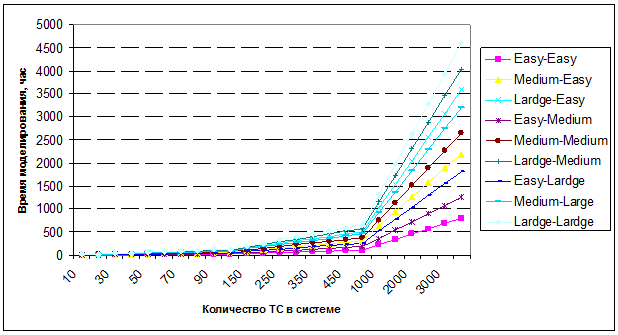
Рис. 4 – Зависимость времени моделирования системы ТС с таблицами, содержащими от 2 до 6 условий (моделирование 1 клиентом БД)
На основании полученных результатов можно сделать вывод, что моделирование системы ТС, включающей таблицы событий с количеством условий от 2 до 10, при количестве таблиц в системе более 10 не целесообразно, ввиду слишком высоких затрат времени на моделирование, за исключением систем, содержащих в ТС только простые условия. В таком случае становится доступным моделирование систем, содержащих до 30 ТС. Для системы ТС с таблицами, содержащими от 2 до 6 условий возможно при количестве ТС в системе до 100 (что составит от 20 до 130 часов машинного времени).
Для оптимизации процесса моделирования, путём снижения времени моделирования, имеет смысл распараллеливать процесс между несколькими клиентами. Так как каждый прогон модели независим, во избежании конфликта при записи информации в банк данных, необходимо и достаточно создать копии БД для каждого параллельного процесса (в терминах обращения БД - клиента). Это увеличит объём базы данных. Проедём расчеты для исследования целесообразности такого моделирования. Пусть параллельно работают 30 клиентов, справедливо предположение, что размер БД при этом значительно увеличится и составит ~ 200% оперативной памяти.
Получим время выполнения транзакции «read-only» и «read-write» для БД размером до 32Гб при конфигурации оборудования HP DL380 G5 (2x Xeon E5450 3Ghz, 16GB DDR2 RAM), Intel S3700 100GB SSD, СУБД PostgreSQL 9.4 для 30 клиентов:
read-only ≈ 9000 транзакций в секунду;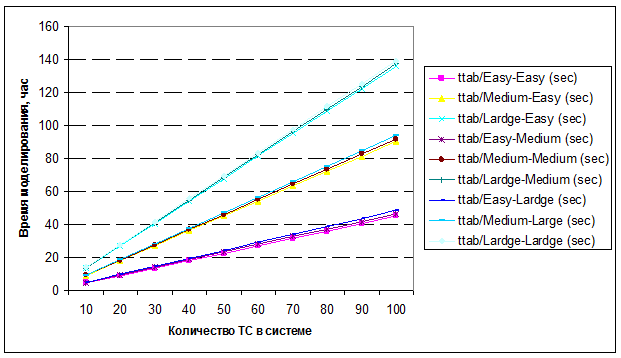
Рис. 5 – Зависимость времени моделирования системы ТС с таблицами, содержащими от 2 до 10 условий (моделирование 30 клиентами БД)
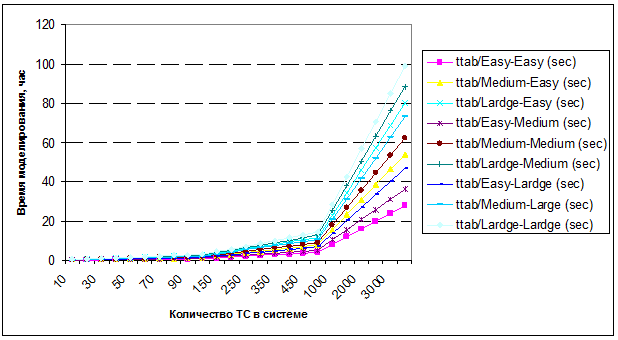
Рис. 6 – Зависимость времени моделирования системы ТС с таблицами, содержащими от 2 до 6 условий (моделирование 30 клиентами БД)
На основании полученных результатов (30 клиентов) можно сделать вывод, что моделирование системы ТС, включающей таблицы событий с количеством условий от 2 до 10, при количестве таблиц в системе до 100 становится достижимым. Для системы ТС с таблицами, содержащими от 2 до 6 условий, при количестве событий в системе до 100 составит до 3 часов машинного времени. При количестве событий в системе до 3000 составит до 100 часов машинного времени.
При моделировании реальной системы нужно учитывать, что при прогоне модели, не все ТС будут задействованы в моделировании. Следовательно, для получения необходимой достоверности моделирование нужно продолжать пока каждая ТС не будет задействована необходимое количество раз.
Полученные в результате исследования данных могут быть использованы при анализе возможности моделирования реальных систем. В том числе и оценки целесообразности подготовки и проведения автоматизированного машинного моделирования.
Литература
- Кулешова О.Н. Разработка методов спецификации информационных моделей средствами языка таблиц событий // Восточно-Европейский журнал передовых технологий. – 2012. № 4/2(58). С. 28–31.
- Боев В. Д., Сыпченко Р. П. Компьютерное моделирование. Лекция 5. Планирование экспериментов. [Электронный ресурс] // НОУ «ИНТУИТ». – URL: http://www.intuit.ru/studies/courses/643/499/lecture/11357 (дата обращения 18.03.2016).
- Володин И.Н. Лекции по теории вероятностей и математической статистике. – Казань: Издательство Казанского государственного университета, – 271с.
- The PostgreSQL Global Development Group: сайт. – URL: https://www.postgresql.org/ (дата обращения 04.2016).
- Tomas Performance since PostgreSQL 7.4 / pgbench. [Электронный ресурс] // PostgreSQL Addict: сайт – http://blog.pgaddict.com/posts/performance-since-postgresql-7-4-to-9-4-pgbench (дата обращения 09.04.2016).
References
- Kuleshova O.N. Razrabotka metodov specifikacii informacionnyh modelej sredstvami jazyka tablic sobytij // Vostochno-Evropejskij zhurnal peredovyh tehnologij. [Development of methods of information models specification by means of the event tables language // Eastern-European journal of enterprise technologies] – 2012. № 4/2(58). P. 28–31.
- Boev V. D., Sypchenko R. P. Komp'juternoe modelirovanie. Lekcija 5. Planirovanie jeksperimentov. [Jelektronnyj resurs] // NOU «INTUIT». [Boev V. D., Sypchenko R. P. Computer Modelling. Lecture 5. Experimental Design. [Electronic resource] // NOU «INTUIT».] – URL: http://www.intuit.ru/studies/courses/643/499/lecture/11357 (date of the application 18.03.2016).
- Volodin I.N. Lekcii po teorii verojatnostej i matematicheskoj statistike. – Kazan': Izdatel'stvo Kazanskogo gosudarstvennogo universiteta [Volodin I.N. Lectures on the theory of probability and mathematical statistics. - Kazan: Publishing House of Kazan State University], – 271p.
- The PostgreSQL Global Development Group: site. – URL: https://www.postgresql.org/ (date of the application 08.04.2016).
- Tomas Vondra. Performance since PostgreSQL 7.4 / pgbench. [Electronic resource] // PostgreSQL Addict: site – http://blog.pgaddict.com/posts/performance-since-postgresql-7-4-to-9-4-pgbench (date of the application 09.04.2016).
