ОБЩИЙ ПОДХОД К РАСЧЕТУ ИЗНОСА ГЛОБОИДНОЙ ПЕРЕДАЧИ
Вяткин А.И.
Кандидат технических наук, Тюменский государственный университет
ОБЩИЙ ПОДХОД К РАСЧЕТУ ИЗНОСА ГЛОБОИДНОЙ ПЕРЕДАЧИ
Аннотация
Предложен алгоритм расчета износа глобоидной передачи, объединяющий модули по расчету полей зазоров в зацеплении, податливости элементов глобоидной пары, распределения нагрузки и расчета износа. В представленной модели процесс износа глобоидного зацепления дискретизируется, при этом предполагается, что износ элементов зацепления во всех контактных точках происходит мгновенно только на границах малого временного интервала, а внутри него соприкасающиеся поверхности считаются неизнашивающимися. Таким образом, задача изменения формы поверхностей зубьев колеса и витков червяка на каждом шаге износа может быть решена при численной реализации принятого подхода.
Ключевые слова: глобоидная передача, износ, шаг износа, фаза зацепления.
Vyatkin A.I.
Assistant professor, PhD in Engineering, Tyumen State University
GENERAL APPROACH TO CALCULATING DEPRECIATION OF GLOBOID TRNSMISSION
Abstract
The article suggests an algorithm for calculating the depreciation of globoid transmission which combines modules for the calculation of the margins gaps in engagement, compliance of globoid pair elements, load distribution and depreciation calculation. In the presented model the process of the globoid engagement depreciation is sampled, in which case one can assume that the wear of the engagement elements in all contact points is instantaneous just on the borders of a small time interval, while within it the mating surfaces are considered wear-free. Thus, the task of changing the shape of the gear teeth surfaces and the worm turns at every depreciation step can be solved by numerical implementation of the approach taken.
Keywords: globoid transmission, depreciation, depreciation step, engagement phase.
К основным функциональным показателям червячных передач с глобоидным червяком, обеспечившим их широкое применение в ряде отраслей техники, следует отнести высокую нагрузочную способность и долговечность, низкую виброактивность и малые энергетические потери. Однако, более высокий, по сравнению с другими видами червячных передач, уровень эксплуатационных свойств глобоидных передач удается, как показал опыт применения и результаты исследований, реализовать только в том случае, если на этапе проектирования выбраны рациональные параметры зацепления и технологические варианты изготовления последнего. В связи с этим при проектировании и изготовлении глобоидных передач возникает ряд сложных проблем, решение которых до сих пор основывалось преимущественно на опыте эксплуатации и экспериментальных исследованиях. Основные функциональные показатели для глобоидных передач, как и для всех видов червячных передач, существенно определяются объективно неблагоприятными условиями трения в зацеплении, а их уровень и, особенно, стабильность работы - износом элементов зацепления. Вследствие этого, указанные исследования и обобщение результатов опыта эксплуатации являются трудоемкими, дорогостоящими и требуют длительного времени.
Современные тенденции развития машиностроения требуют большего учета конкретных условий эксплуатации глобоидных передач, расширения разнообразия их типоразмеров и вариантов зацепления, технологических способов изготовления его элементов. В этих условиях сокращение затрат и времени на выбор параметров зацепления, вариантов технологических процессов при его изготовлении, контроле и доводке может быть достигнуто за счет применения методов компьютерного моделирования и проектирования. В данной работе предложен общий подход к разработке эволюционной модели износа глобоидного зацепления.
Упрощенная блок-схема расчета модели износа глобоидного зацепления представлена на рис. 1, объединяющая модули по расчету полей зазоров в зацеплении, податливости элементов глобоидной пары, распределения нагрузки и расчета износа [1].
В качестве исходной принята расчетная схема глобоидного зацепления, представляющая систему зубьев колеса и витков червяка, контактирующих между собой. Предполагается, что зубья и витки являются деформируемыми телами, рабочие поверхности которых изменяют свою форму в процессе износа. Число контактирующих зубьев и витков червяка считается переменным, зависящим от внешней нагрузки и от относительного положения колеса и червяка. Принято, что мгновенное относительное положение колеса и червяка определяется не только обобщенной координатой механизма, но и погрешностями формообразования зубьев колеса и витков червяка, погрешностями монтажа, деформациями и износом деталей передачи (включая колесо и червяк).
В качестве обобщенной координаты зацепления выбран угол поворота червяка, который далее называется фазой зацепления. Считается, что нагрузка приложена к колесу в виде внешнего момента, а момент на червяке определяется из условия обеспечения заданного движения. При описании и анализе выбранной модели глобоидного зацепления внутренние динамические процессы не учитываются, внешние - могут быть учтены при задании нагрузки. Таким образом, предполагается, что глобоидное зацепление функционирует в квазистатических условиях.
В соответствии с выбранным подходом непрерывный процесс износа дискретизируется. При этом предполагается, что износ элементов зацепления во всех контактных точках происходит мгновенно, только на границах малого временного интервала, а внутри него соприкасающиеся поверхности считаются неизнашивающимися. Естественно возникает вопрос о временной продолжительности этого дискретного состояния или продолжительности шага износа. Является очевидным, что чем меньше длительность шага износа, тем точнее будет моделироваться процесс износа. Однако время шага износа не может быть бесконечно малым, поскольку возможности ЭВМ ограничены. В связи с этим за шаг износа взято время, в течение которого максимальный износ сопряжения ∆Н станет численно равным сумме высот микронеровностей рабочих поверхностей витков червяка (Rz1) и зубьев колеса (Rz2). Значения R берутся из рабочих чертежей. Для рассматриваемой передачи эта сумма равнялась 10 мкм.
Широко известно, что в период приработки износ изменяется по нелинейному закону (рис.2), отсюда и шаг износа будет переменным. За минимально возможный шаг износа взято время, соответствующее длительности одного цикла зацепления, которое вычисляется в зависимости от геометро-кинематических параметров передачи и режима нагружения. Например, для рассматриваемой глобоидной передачи, с числом заходов равным единице и постоянным моментом нагружения на валу червячного колеса, за цикл зацепления одного зуба колеса с витком червяка принято время прохождения зуба колеса с момента входа зуба колеса в зацепление с витком червяка до полного его выхода из зацепления, при этом зуб колеса последовательно проходит фиксированные расчетные фазы зацепления (для данного типоразмера передачи -17 фаз). Время цикла зацепления червяка с червячным колесом будет равно времени одного оборота колеса.
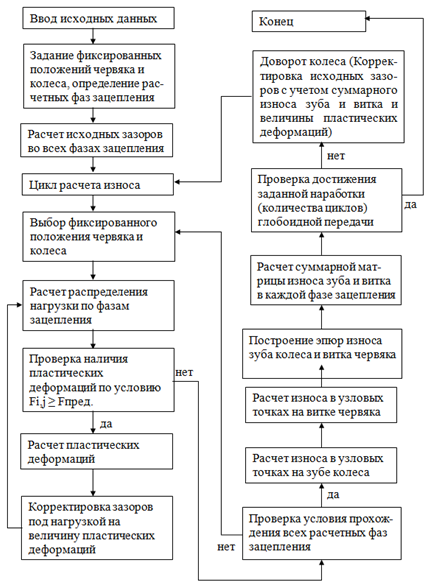
Рис. 1 – Блок-схема расчета износа глобоидной передачи
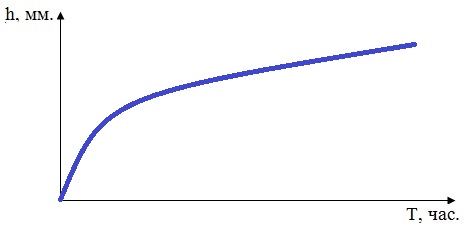
Рис. 2 – Характер изменения износа сопряжения h в период приработки T
При соблюдении условия ∆hmax ≥ ∆Н, где ∆hmax - максимальный износ сопряжения за цикл зацепления червяка (в рассматриваемой передаче за один оборот колеса) шаг износа равен времени одного цикла зацепления червяка с колесом. Если ∆hmax ≤ ∆Н, то вычисляется коэффициент:
N=∆Н/∆hmax (1)
Шаг износа вычислялся по зависимости:
tизн = Ntц , (2)
где tц - время одного цикла зацепления червяка;
tизн - временной интервал, соответствующий шагу износа.
Информация о величине шага износа принципиально позволяет решить задачу расчета ресурса.
Принято, что износ в каждой контактной точке поверхностей колеса и червяка в начальной и конечной фазе шага износа определяется по зависимости [2]:
∆hi,j = Ji,j∆Li,j (3)
где i,j - индексы, соответствующие положению контактной точки на поверхностях зуба колеса и витка червяка; ∆Li,j - путь трения для выбранной точки зуба колеса (витка червяка); Ji,j - интенсивность износа материала зубьев колеса (витка червяка) на данном шаге расчета износа.
Для определения интенсивности износа использовалось известное соотношение /3/:
Ji,j = K12Pij /HB (4)
где Pij - нормальное контактное давление в той же точке; НВ - твердость материала зубьев колеса (витков червяка).
Входящий в соотношение (4) коэффициент K12, характеризующий износостойкость материалов колеса и червяка, условия трения и изнашивания в рассматриваемой точке и определяемый расчетным или экспериментальным путем, предполагается заданным при построении и использовании модели износа.
Поскольку ∆hi,j представляет собой линейный износ в направлении нормали к поверхности, изменения декартовых координат точки поверхности зуба колеса и витка червяка за шаг износа могут быть определены из соотношений:
∆X = ∆hi,jex; ∆Y = ey; ∆Z = ∆hi,jez; (5)
где, e(еx, еy, еz ) - орт нормали к соответствующей поверхности в контактной точке.
Используя выражение (1) и (3) получаем зависимость для износа зубьев колеса в виде:
∆h2ij = NJ2ij∆L2ij (6)
где индекс 2 определяет принадлежность к колесу.
При определении износа витка червяка следует иметь ввиду, что на один цикл зацепления витка червяка приходится i циклов зацепления зуба колеса, где i - передаточное число. Поэтому зависимость определения износа (3) в окончательном виде перепишется в следующем виде:
∆h2ij = iNJ2ij∆L2ij (7)
Таким образом, задача об изменении формы поверхностей зубьев колеса и витков червяка на каждом шаге износа может быть решена при численной реализации принятого подхода, если известны величины, входящие в выражения (3),(4),(5) и вид зависимости (5).
Список литературы / References
- Вяткин А.И. Разработка и анализ расчетно-эволюционной модели износа глобоидного зацепления. : дис. … канд. тех. наук : 05.02.02 : защищена 03.10.97 : утв. 16.01.98 / Вяткин Александр Игоревич. – Курган, 1997. – 220 с.
- Гриб В.В. Решение триботехнических задач численными методами. - М.: Наука, 1982. - 112с.
- Хрущов М.М., Бабичев М.А. Исследование изнашивания металлов. - М.: АН СССР, 1960. – 64 с.
Список литературы на английском языке / References in English
- Vyatkin A.I. Razrabotka i analiz raschetno-ehvolyucionnoj modeli iznosa globoidnogo zacepleniya [Development and analysis of computational and evolutionary model of globoid engagement depreciation] : dis. … of PhD in Engineering : 05.02.02. : defense of the thesis 03.10.97 : approved 16.01.98 / Vyatkin Aleksandr Igorevich. – Kurgan, 1997. – 220 p. [in Russian]
- Grib V.V. Reshenie tribotekhnicheskih zadach chislennymi metodami [The solution of tribological problems by numerical methods] / V.V. Grib. – M : Nauka, 1982. – 112 p. [in Russian]
- Khrushchov M.M., Babichev M.A. Issledovanie iznashivaniya metallov [Metal depreciation study] / M.M. Krushchov, M.A. Babichev. – M : AN SSSR, 1960. – 64 p. [in Russian]
