МОДИФИКАЦИЯ КРИТЕРИЯ КУЛОНА – МОРА ДЛЯ РАСЧЕТА КОНСТРУКЦИЙ ЛЕСНЫХ ДОРОГ ПО СОПРОТИВЛЕНИЮ СДВИГУ. ЧАСТЬ 2. ТРЕХОСНЫЕ ИСПЫТАНИЯ И ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ ТРЕТЬЕГО ПАРАМЕТРОВ МАТЕРИАЛА
Александров А.С.
ORCID: 0000-0003-2009-5361, Кандидат технических наук, Сибирская государственная автомобильно-дорожная академия
МОДИФИКАЦИЯ КРИТЕРИЯ КУЛОНА – МОРА ДЛЯ РАСЧЕТА КОНСТРУКЦИЙ ЛЕСНЫХ ДОРОГ ПО СОПРОТИВЛЕНИЮ СДВИГУ. ЧАСТЬ 2. ТРЕХОСНЫЕ ИСПЫТАНИЯ И ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ ТРЕТЬЕГО ПАРАМЕТРОВ МАТЕРИАЛА
Аннотация
В статье приведена методика испытания грунтов трехосным сжатием, позволяющая определить величину третьего параметра модифицированного условия пластичности Кулона – Мора. Выполнено математическое моделирование зависимости этого параметра от вертикальной деформации образца при трехосном сжатии. Даны рекомендации, дополняющие данные нормативных документов по проектированию дорожных одежд, о значениях параметров грунтов при их оценке по сопротивлению сдвигу.
Ключевые слова: дорога, лесная дорога, грунт, сопротивление сдвигу, условие пластичности.
Aleksandrov A.S.
ORCID: 0000-0003-2009-5361, PhD in Engineering, Siberian State Automobile and Highway Academy
MODIFICATION OF COULOMB – MOHR CRITERIA FOR CALCULATION OF CONSTRUCTION OF FOREST ROADS IN SHEAR RESISTANCE. PART 2. TRIAXIAL AND DETERMINATION OF THE THIRD MATERIAL PARAMETERS
Abstract
The paper describes the method of testing soil by triaxial compression, which allows to determine the value of the third parameter of the modified conditions of Coulomb - Mohr plasticity. Authors performed mathematical modeling of the dependence of this parameter on the vertical deformation of the sample under triaxial compression. Recommendations were given complementing the regulatory documents on designing pavements, on the values of soil parameters for their evaluation of the shear strength.
Keywords: road, forest road, soil shear strength, plasticity condition.
Недостаточное сопротивление грунтов и дискретных материалов сдвигу приводят к существенным пластическим деформациям земляного полотна, что обуславливает ухудшение ровности покрытия в течение эксплуатации автомобильной дороги. Снижение ровности дорожных покрытий приводит к снижению основных транспортно-эксплуатационных показателей автомобильной дороги. При достаточно низких скоростях движения возрастает объем выброса выхлопных газов, образуемых при сжигании топлива. Поэтому уменьшение скорости движения транспортных средств обуславливает ухудшение экологической безопасности. Отсюда следует актуальность работ, направленных на разработку методов расчета деформационно-устойчивых дорожных одежд, покрытия которых сохраняют требуемую ровность в течение всего срока службы. Анализ работ предшественников показывает, что обозначенная автором проблема, решается в двух направлениях. Во-первых, выполняется разработка расчетных методик, позволяющих прогнозировать процесс накапливания пластических деформаций в грунтах и зернистых материалах, а также выполнять расчеты изменения показателей ровности дорожных покрытий и определять межремонтные сроки. Математические модели пластического деформирования грунтов и дискретных материалов можно подразделить по виду функции, связывающей накапливаемую деформацию с числом нагрузок, и количеством параметров материала. Используя этот классификационный признак, отметим, что модели накапливания деформаций подразделяются на:
– логарифмические однопараметрические [1, C. 6], [2, С. 251-252];
– логарифмические двухпараметрические [3, C. 82], [4, C. 28], [5, С. 2-19];
– степенные двухпараметрические [4, C. 28], [6, С. 45];
– степенные трехпараметрические [4, C. 28], [7, С. 278];
– экспоненциальные двух и трехпараметрические [8, С. 252], [9, С. 1138].
Методики расчета глубины неровностей можно подразделить на методы, позволяющие вычислять показатели ровности дороги, которые измеряют при диагностике [10, С. 50], [11, С. 488],и решения позволяющие вычислять пластические смещения в сечении по оси симметрии нагрузки или в любой точке дорожной конструкции [12, С. 175 – 246], [13, С. 22-30], [14, С. 176-179].
Во-вторых, предпринимаются разработки методики проектирования дорожных конструкций по критерию сопротивления сдвигу в грунте земляного полотна и слоях дорожной одежды из гранулированных (зернистых) материалов. Такие методы можно подразделить на способы расчета критических нагрузок, использующие в своей основе модель линейно-деформируемой среды [15, С. 95], [16, С. 115] и метод предельного равновесия механики грунтов [17, С. 250], [18, С. 6], [19, С. 115].
В целях совершенствования методики ОДН 218.046-01, предназначенной для расчета дорожной конструкции по сопротивлению сдвигу в грунте земляного полотна и конструктивных слоях оснований и покрытий дорожных одежд, выполненных из гранулированных материалов, нами предложен модифицированный вводом третьего параметра критерий пластичности. Уравнение предельного состояния предлагаемого критерия имеет вид:
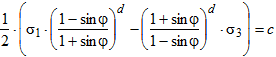 (1)
(1)
Где σ1 и σ3 – максимальное и минимальное главные напряжения, возникающие в наиболее опасной точке сечения, расположенного по оси симметрии нагрузки, Па; с и φ – сцепление и угол внутреннего трения, Па и о соответственно; d – третий параметр материала, введенный автором.
Параметр d введен для варьирования величины касательного напряжения, определяемого левой частью уравнения (1). Примечательно, что при d=0,5 касательные напряжения, вычисляемые по формуле (1) совпадают с касательными напряжениями оригинального критерия Кулона–Мора. При d=0 уравнение (1) преобразуется к виду третьей теории прочности, а касательное напряжение достигает величины максимального касательного напряжения и определяется половиной разности максимального и минимального главных напряжений. Зависимости для расчета касательных напряжений при различной величине параметра d приведены в табл. 1.
Таблица 1 – Формулы для расчета касательных напряжений

При построении кругов предельных напряжений для критерия, описываемого уравнением (1) можно отметить диаметрально противоположную картину. Круги предельных напряжений достигают максимального размера при d=0,5. Демонстрируя эту особенность уравнение предельного равновесия (1) решим относительно величины максимального главного напряжения σ1, подразумевая, что при заданных c, φ, d и σ3, рассчитываемое максимальное главное напряжение является предельным для данного грунта. Решив уравнение (1) относительно s1, получим формулу для вычисления его предельной величины:
![]() (2)
(2)
Диаметр каждого круга предельных напряжений определяется девиатором предельных напряжений, то есть разностью предельной величины максимального касательного напряжения σ1пр и минимального главного напряжения, при которых произошел отказ образца при трехосных испытаниях. Радиус кругов предельных напряжений вычисляют как половину диаметра. Таким образом, диаметр и радиус кругов предельных напряжений вычислим по формулам:
![]() (3)
(3)
Для построения кругов предельных напряжений примем, что сцепление и угол внутреннего трения при предельной деформации образца 15 % составляют 30 кПа и 20 о соответственно. Величину параметра d будем варьировать и примем для кругов первого семейства d=0,5, для кругов второго семейства d=0,3, а для кругов третьего семейства d=0. Круги предельных напряжений построим для двух значений минимального главного напряжения σ3=50 кПа и σ3=200 кПа. Задавшись такими исходными данными, по формуле (2) вычислим значения предельной величины максимального главного напряжения σ1пр. Для кругов первого семейства для случая σ3=50 кПа и при величине третьего параметра d=0,5, d=0,3 и d=0 получим, что σ1пр=187,669 кПа, σ1пр=150,987 кПа, σ1пр=110 кПа. Для кругов предельных напряжений второго семейства, рассчитываемых для случая σ3=200 кПа и при тех же значениях параметра d, получим, что σ1пр=493,61 кПа при d=0,5, σ1пр=381,036 кПа при d=0,3 и σ1пр=160 кПа при d=0. По формулам (3) вычислим диаметр и радиус каждого из шести кругов предельных напряжений. Абсциссу каждого из центров кругов определим половиной суммы предельного максимального главного напряжения и соответствующего ему минимального главного напряжения, то есть по формуле:
![]() (4)
(4)
Анализируя формулу (4) укажем, что величина Апр равна значению нормального напряжения действующего на площадку, вдоль которой действует максимальное касательное напряжение, которое на графике определяется радиусом круга предельных напряжений. На рис. 1 приведены построенные по данным расчета круги предельных напряжений, которые обозначены цифрами 1–3 (круги первого семейства, соответствующие σ3=50 кПа) и 4–6 (круги второго семейства для случая σ3=200 кПа). К каждой из трех пар кругов проведена предельная прямая.
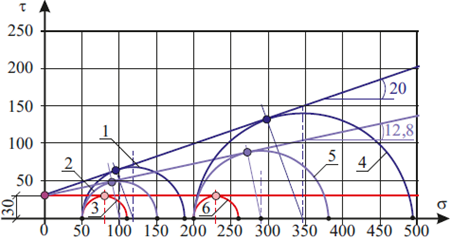
Рис. 1 – Круги предельных напряжений. 1–3 при σ3=50 кПа и d 0,5; 0,3 и 0; 4–6 при σ3=200 кПа и d 0,5; 0,3 и 0
Из анализа предельных прямых, построенных на рис. 1, следует, что они характеризуются одинаковым сцеплением, но разными углами внутреннего трения. Поэтому параметр d позволяет варьировать радиус, диаметр и абсциссу центра кругов предельных напряжений. В опытах по трехосному сжатию грунтов такое варьирование происходит при изменении предельной деформации. Круг предельных напряжений уменьшается при уменьшении деформации принимаемой за предельную величину. Построение предельных прямых Кулона–Мора к кругам предельных напряжений, полученных из анализа экспериментальных данных, приводит к тому, что изменяется как угол внутреннего трения, так и сцепление. Из данных рис. 1 следует, что у предельных прямых изменяется только угловая координата, а сцепление остается одинаковым. Эта особенность предельных прямых к кругам предельных напряжений, построенных по предлагаемому критерию (1) и тождественной ему формуле (2) отличает их от своих аналогов, построенных к кругам предельных напряжений оригинального критерия пластичности Кулона – Мора. Эта особенность предлагаемого уравнения предельного равновесия позволяет использовать нормативные значения сцепления и угла внутреннего трения, которые регламентируются ОДН 218.046-01.
С одной стороны достоинство такое отличия состоит в возможности использования надежной и достоверной базы данных о сцеплении и угле внутреннего трения различных дисперсных грунтов, а с другой стороны ставит задачу экспериментального определения величины параметра d.
Для решения этой задачи нами проанализированы данные публикаций [20, С. 70], [21, С. 1211], в которых экспериментально установлено, что в процессе трехосного сжатия грунта при деформировании образца на величину 8 % в нем происходит зарождение площадок сдвига, а при дальнейшем деформировании вдоль этих площадок локализуются пластические деформации, которые обуславливают окончательное формирование площадок скольжения. При дальнейшем деформировании образцы испытывают пластическое течение и могут приобретать деформацию 20 % и более. Таким образом, величина опасной деформации ε1 находится в диапазоне от 8–12 %, а при трехосных испытаниях предельную деформацию ε1с ограничивают 15 % в РФ и 20 % за рубежом. Если деформации в ε1=8 % и ε1=12 % разделим на предельную величину деформации ε1с=15 %, то получим ε1/ε1с=0,5 и ε1/ε1с =0,8, на основание чего можно утверждать, что опасные сдвиговые деформации составляют 50–80 % от предельной деформации трехосных испытаний. Рассмотренные нами отношения e1/e1с=0,5 и ε1/ε1с=0,8 позволяют классифицировать условия работы грунта. Например, при ε1/ε1с<0,5 имеет место объемной упругопластическое сжатие грунтового образца, существенно преобладает над деформациями сдвига. Такое состояние можно считать безопасным. При варьировании показателя ε1/ε1с в диапазоне 0,5≤ε1/ε1с≤0,8 локализуются деформации сдвига, и их доля постоянно возрастает при увеличении отношения ε1/ε1с от значения 0,5 до величину 0,8. Так как деформации сдвига является пластическими, то их рост приводит к увеличению доли пластической деформации в общей упругопластической деформации образца. Такую фазу деформирования можно назвать стадией сдвига или стадией локализации необратимых (пластических) деформаций. Рассматривая деформирование при показателе ε1/ε1с>0,8, отметим, что преобладающим типом деформаций являются деформации сдвига, обуславливающие пластическое течение образца. Эта стадия деформирования является запредельной фазой работы грунта.
Суть экспериментов по трехосному сжатию грунтов заключалась в выполнении испытаний по схемам консолидированного недренированного и неконсолидированного недренированного тестов. Оба теста выполнены для грунтовых образцов близнецов, изготовленных из одного и того же грунта с одинаковым коэффициентом уплотнения, так же одной и той же влажностью. Обработкой результатов консолидированного недренированного теста определяли сцепление и угол внутреннего трения грунта, следуя методики государственного стандарта. Неконсолидированный недренированный тест применяли для определения параметра d. Его результаты представляли в виде зависимости деформации от главных напряжений. По графику определяли величину главных напряжений, которой соответствуют деформации ε1=0,5×ε1с, ε1=0,6×ε1с, ε1=0,7×ε1с и ε1=0,8×ε1с. По формуле (2) вычисляли предельную величину максимального главного напряжения, варьируя параметр d в диапазоне от 0,5 до 0, а сцепление и угол внутреннего трения принимали по данным консолидированных недренированных испытаний при таком же значении минимального главного напряжения. Вычисленные по формуле (2) значения сравнивали с экспериментальным значением. В результате удалось определить значения параметра d, при которых результаты вычисления предельной величины максимального главного напряжения по зависимости (2) соответствуют экспериментальным значениям этого напряжения при различном относительном показателе ε1/ε1с. Отсюда был сделан вывод о связи параметра d и отношения ε1/ε1с. Далее для каждого из четырех значений отношения ε1/ε1с была сформирована выборка частных значений параметров d. После формирования выборок их проверили на наличие грубых ошибок, и убедившись в том, что их нет определили коэффициент вариации и расчетные значения этого параметра при двухсторонней доверительной вероятности 95 %.
Вычисленные статистики приведены в табл. 2.Таблица 2 – Результаты статистической обработки параметра d
| Статистика | Отношение деформаций ε1/ε1с | |||
| 0,5 | 0,6 | 0,7 | 0,8 | |
| Статистики новых выборок после попарного объединения | ||||
| dср | 0,314 | 0,372 | 0,420 | 0,459 |
| Sd | 0,050 | 0,053 | 0,050 | 0,046 |
| V,% | 16,03 | 14,17 | 11,95 | 9,94 |
| dmin | 0,295 | 0,352 | 0,401 | 0,442 |
| dmax | 0,333 | 0,392 | 0,439 | 0,477 |
Статистические значения параметра dв зависимости от относительной характеристики ε1/ε1с аппроксимированы формулами
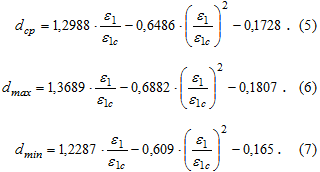
Используя математические модели (5) – (7), можно выполнять вычисления среднего выборочного или расчетного значения параметра d для необходимого отношения ε1/ε1с. Значения этого параметра дополняют данные ОДН 218.046-01 о сцеплении и угле внутреннего трения грунтов.
Обсуждая пути дальнейшего совершенствования критерия (1) отметим два перспективных направления, связанных с учетом влияния показателей физических свойств грунтов и усталостных процессов на параметры материала в предлагаемом критерии. Реализация учета влияния показателей физических свойств на пластичность может быть выполнена вводом математических моделей зависимости угла внутреннего трения и сцепления от коэффициента уплотнения и влажности грунта в уравнение (1). Такие модели можно заимствовать из публикаций [22, С. 11] и [23, С. 452]. Влияние усталостных процессов учитывается вводом параметров теории поврежденности в левую часть уравнения (1). Параметры этой теории являются функцией числа повторных нагрузок. Принципы вывода этих функциональных зависимостей приведены в работах [24, С. 75-77], [25, С. 273] и [26, С. 353]. Применяя методы и математические модели, опубликованные в статьях [23–27] условие пластичности (1) модифицируется так, что в нем учитываются физические характеристики грунтов и повторность приложения транспортных нагрузок. Такое совершенствование критерия (1) можно считать задачей дальнейших исследований.
Список литературы / References
- Васильев А.П. Предложения по учету остаточных деформаций при расчете дорожных одежд нежесткого типа / А. П. Васильев// Наука и техника в дорожной отрасли. – 1997. – №1. – С. 5–6.
- Семенова Т.В.. Определение пластических деформаций материалов, используемых в дорожных конструкциях / Т. В. Семенова, С. А. Гордеева, В. Н. Герцог // Вестник Томского государственного архитектурно-строительного университета. – 2012. – №4 (37). – С. 247-254.
- Barksdale R.D. Performance of Crushed-Stone Base Courses. Transportation Research Record, 954, Transportation Research Board, Washington, D. C. – 1984. –p. 78-87.
- Александров А.С. Исследование пластического деформирования дискретных материалов при воздействии циклических нагрузок и определение параметров математических моделей / А. С. Александров // Строительные материалы. – 2016. – № 10. – С. 27-32.
- Werkmeister S. Permanent deformation behavior of unbound granular materials in pavement constructions // Ph.D. thesis, University of Technology, Dresden, The Germany. 2003.
- Arnold G.K. Rutting of Granular Pavements. // Thesis submitted to The University of Nottingham for the degree of Doctor of Philosophy, November 2004. – 417 p.
- Aleksandrov A.S., Semenova T.V., Aleksandrova N.P. Analysis of permanent deformations in granular materials of road structures. // Road and Bridges - Drogi i Mosty, 2016, Vol. 15, Pp 263 – 276.
- Niemunis A., Wichtmann T., Triantafyllidis T. A high-cycle accumulation model for sand. // Computers and Geotechnics, 2005. Vol. 32, No4, Pp. 245-263.
- Niemunis A., Wichtmann T. (2014): Separation of time scale in the HCA model for sand. // Acta Geophysica, Vol. 62, No. 5, pp. 1127-1145.
- Герцог В.Н. Расчет дорожных одежд по критериям ровности. Часть 1. Обоснование норм ровности асфальтобетонных покрытий / В. Н. Герцог, Г. В. Долгих, В. Н. Кузин // Инженерно-строительный журнал. – 2015. – №5 (57) – С. 45-57.
- K., Sun, L.J., Hachiya, Y. Rut Prediction for Semi-rigid Asphalt Pavements // First International Symposium on Transportation and Development Innovative Best Practices. – 2008. – Beijing. pp. 486-491.
- Матуа В.П. Прогнозирование и учет накопления остаточных деформаций в дорожных конструкциях / В. П. Матуа, Л. Н. Панасюк. – Ростов-на-Дону: РГСУ, 2001. – 372 с.
- Матуа В.П. Исследование напряженно-деформированного состояния дорожных конструкций с учетом их неупругих свойств и пространственного нагружения: автореферат … д-ра техн. наук / В. П. Матуа. – Ростов-на-Дону: Изд-во РГСУ, 2002. – 40 с.
- Матуа В.П. Комплексный подход к решению проблемы колееобразования на федеральных автомобильных дорогах Российской / В. П. Матуа, Д. В. Чирва, Р. В. Матуа // Второй Всероссийский дорожный конгресс – М.: МАДИ, 2010. – С. 176-180.
- Долгих Г.В. Определение первой критической нагрузки при расчете грунтов земляного полотна по сопротивлению сдвигу / Г. В. Долгих // Вестник Московского автомобильно-дорожного государственного технического университета (МАДИ). – 2016.– № 3 (46). – С. 90-97.
- Долгих Г. В.Применение безопасного давления в качестве критерия расчета земляного полотна по сдвигу в грунте / Г. В. Долгих // В сборнике: Наука XXI века: опыт прошлого -взгляд в будущее: материала II международной научно-практической конференции -Омск, СибАДИ, 2016. -С. 113-117.
- Burd H.J., Frydman S. Bearing capacity of plane-strain footings on layered soils. Geotech. J. 1997. vol. 34. Pp. 241-253.
- Meyer N., Elias J.M. Design methods for roads reinforced with multifunctional geogrid composites for sub-base stabilization. German Conference on Geosynthetics, Technical University Munich. 1999. Pp. 1-8.
- Benjamin C.V.S., Bueno B., Zornberg J.G. Field monitoring evaluation of geotextile-reinforced soil retaining walls. Geosynthetics International Journal. 2007. vol. 14. No. 2. Pp. 100-118.
- Oka, F. Computational modeling of large deformations and failure of geomaterials. /XVI ICSMGE, Osaka 2005. – Millpress Vol. 1. – Pp. 47 – 94.
- Higo, Y., et al. A three-dimensional elasto-viscoplastic strain localization analysis of water-saturated clay // Geo-Research Institute, Osaka, Japan. Vol. 86, 2006. – рр. 3205-3240.
- Семенова Т.В. Совешенствование методов экспресс контроля уплотнения грунтов в земляном полотне лесных дорог. Часть 1. Обобщающая математическая модель / Т. В. Семенова, Н. П. Александрова // Международный научно-исследовательский журнал. –2016.– № 6-2 (48). – С. 10-14.
- Семенова Т.В. Влияние влажности и степени уплотнения грунта земляного полотна на параметры прочности и деформируемости / Т. В. Семенова, Н. В. Кузин // Научный альманах. – 2016.– № 7-1 (21). – С. 451-454.
- Aleksandrova N.P., Chysow V.V. The usage of integral equations hereditary theories for calculating changes of measures of the theory of damage when exposed to repeated loads // Magazine of Civil Engineering. – 2016.– № 2 (62). – P. 69-82.
- Чусов В. В.Два способа расчета мер теории накапливания повреждений / В. В. Чусов , Н. П. Александрова // В сборнике: Наука XXI века: опыт прошлого -взгляд в будущее: материала II международной научно-практической конференции -Омск, СибАДИ, 2016 -С. 271-275.
- Александрова Н. П. Применение принципа эквивалентности деформаций к задаче расчета мер теории поврежденности в условии пластичности асфальтобетона / Н. П. Александрова, Н. В. Кузин, В. В. Чусов // Научный альманах. – 2016. – № 7-1 (21). – С. 352-356.
Список литературы на английском языке / References in English
- Vasil'ev A.P. Predlozhenija po uchetu ostatochnyh deformacij pri raschete dorozhnyh odezhd nezhestkogo tipa [Proposals for integration of the residual strain in the calculation of non-rigid pavements type] / A. P. Vasil'ev// Nauka i tehnika v dorozhnoj otrasli [Science and Engineering for Highways]. – 1997. – №1. – P. 5–6. [in Russian]
- Semenova T.V.. Opredelenie plasticheskih deformacij materialov, ispol'zuemyh v dorozhnyh konstrukcijah [Determination of plastic deformation of materials used in road constructions] / T. V. Semenova, S. A. Gordeeva, V. N. Gercog // Vestnik Tomskogo gosudarstvennogo arhitekturno-stroitel'nogo universiteta [Bulletin Tomsk State University of Architecture and Building]. – 2012. – №4 (37). – P. 247-254. [in Russian]
- Barksdale R.D. Performance of Crushed-Stone Base Courses. Transportation Research Record, 954, Transportation Research Board, Washington, D. C. – 1984. –p. 78-87.
- Aleksandrov A.S. Issledovanie plasticheskogo deformirovanija diskretnyh materialov pri vozdejstvii ciklicheskih nagruzok i opredelenie parametrov matematicheskih modelej [A Generalizing model of plastic deformation of discrete materials of road structures under impact of cyclic loads] / A. S. Aleksandrov // Stroitel'nye materialy [Construction Materials]. – 2016. – № 10. – P. 27-32. [in Russian]
- Werkmeister S. Permanent deformation behavior of unbound granular materials in pavement constructions // Ph.D. thesis, University of Technology, Dresden, The Germany. 2003.
- Arnold G.K. Rutting of Granular Pavements. // Thesis submitted to The University of Nottingham for the degree of Doctor of Philosophy, November 2004. – 417 p.
- Aleksandrov A.S., Semenova T.V., Aleksandrova N.P. Analysis of permanent deformations in granular materials of road structures. // Road and Bridges - Drogi i Mosty, 2016, Vol. 15, Pp 263 – 276.
- Niemunis A., Wichtmann T., Triantafyllidis T. A high-cycle accumulation model for sand. // Computers and Geotechnics, 2005. Vol. 32, No4, Pp. 245-263.
- Niemunis A., Wichtmann T. (2014): Separation of time scale in the HCA model for sand. // Acta Geophysica, Vol. 62, No. 5, pp. 1127-1145.
- Gercog V.N. Raschet dorozhnyh odezhd po kriterijam rovnosti. Chast' 1. Obosnovanie norm rovnosti asfal'tobetonnyh pokrytij [Calculation of pavements for roughness criteria. Part 1. Justification standards evenness of asphalt-concrete coatings] / V. N. Gercog, G. V. Dolgih, V. N. Kuzin // Inzhenerno-stroitel'nyj zhurnal [Magazine of Civil Engineering]. – 2015. – №5 (57) – P. 45-57. [in Russian]
- , K., Sun, L.J., Hachiya, Y. Rut Prediction for Semi-rigid Asphalt Pavements // First International Symposium on Transportation and Development Innovative Best Practices. – 2008. – Beijing. pp. 486-491.
- Matua V.P. Prognozirovanie i uchet nakoplenija ostatochnyh deformacij v dorozhnyh konstrukcijah [Forecasting and accumulated residual strains in road structures] / V. P. Matua, L. N. Panasjuk. – Rostov-na-Donu: RGSU, 2001. – 372 p. [in Russian]
- Matua V.P. Issledovanie naprjazhenno-deformirovannogo sostojanija dorozhnyh konstrukcij s uchetom ih neuprugih svojstv i prostranstvennogo nagruzhenija [Investigation of stress-strain state of the road constructions in view of their non-elastic properties and spatial load] : … of PhD in Engineering : 05.23.11 / V. P. Matua. – Rostov-na-Donu: Izd-vo RGSU, 2002. – 40 p. [in Russian]
- Matua V.P. Kompleksnyj podhod k resheniju problemy koleeobrazovanija na federal'nyh avtomobil'nyh dorogah Rossijskoj [On federal roads integrated approach to solving the problems of the Russian rutting] / V. P. Matua, D. V. Chirva, R. V. Matua // Vtoroj Vserossijskij dorozhnyj congress[Second All-Russia Congress of road] – M.: MADI, 2010. – P. 176- 180. [in Russian]
- Dolgih G.V. Opredelenie pervoj kriticheskoj nagruzki pri raschete gruntov zemljanogo polotna po soprotivleniju sdvigu [Determination of the first critical load in the calculation of subgrade soil on shear strength] / G. V. Dolgih // Vestnik Moskovskogo avtomobil'no-dorozhnogo gosudarstvennogo tehnicheskogo universiteta (MADI) [Bulletin of the Moscow State Automobile and Road Technical University (MADI).]. 2016. № 3 (46). P. 90-97. [in Russian]
- Dolgih G. V. Primenenie bezopasnogo davlenija v kachestve kriterija rascheta zemljanogo polotna po sdvigu v grunte [The use of safe pressure as a criterion for calculating the subgrade for a shift in the soil] / G. V. Dolgih // V sbornike: Nauka XXI veka: opyt proshlogo -vzgljad v budushhee: materiala II mezhdunarodnoj nauchno-prakticheskoj konferencii [In: Science of the XXI century: -vzglyad past experience into the future: the material of the II International Scientific and Practical Conference] -Omsk, SibADI, 2016. -P. 113-117. [in Russian]
- Burd H.J., Frydman S. Bearing capacity of plane-strain footings on layered soils. Geotech. J. 1997. vol. 34. Pp. 241-253.
- Meyer N., Elias J.M. Design methods for roads reinforced with multifunctional geogrid composites for sub-base stabilization. German Conference on Geosynthetics, Technical University Munich. 1999. Pp. 1-8.
- Benjamin C.V.S., Bueno B., Zornberg J.G. Field monitoring evaluation of geotextile-reinforced soil retaining walls. Geosynthetics International Journal. 2007. vol. 14. No. 2. Pp. 100-118.
- Oka, F. Computational modeling of large deformations and failure of geomaterials. /XVI ICSMGE, Osaka 2005. – Millpress Vol. 1. – Pp. 47 – 94.
- Higo, Y., et al. A three-dimensional elasto-viscoplastic strain localization analysis of water-saturated clay // Geo-Research Institute, Osaka, Japan. Vol. 86, 2006. – рр. 3205-3240.
- Semenova T.V. Soveshenstvovanie metodov jekspress kontrolja uplotnenija gruntov v zemljanom polotne lesnyh dorog. Chast' 1. Obobshhajushhaja matematicheskaja model' [Improvement of methods for monitoring the express compacted soil subgrade forest roads] / T. V. Semenova, N. P. Aleksandrova // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal [International Research Journal]. –2016. – № 6-2 (48). – P. 10-14. [in Russian]
- Semenova T.V. Vlijanie vlazhnosti i stepeni uplotnenija grunta zemljanogo polotna na parametry prochnosti i deformiruemosti [Influence of moisture content and degree of compaction of subgrade on the parameters of strength and deformability] / T. V. Semenova, N. V. Kuzin // Nauchnyj al'manah [Science Almanac]. – 2016. – № 7-1 (21). – P. 451-454. [in Russian]
- Aleksandrova N.P., Chysow V.V. The usage of integral equations hereditary theories for calculating changes of measures of the theory of damage when exposed to repeated loads // Magazine of Civil Engineering. – 2016.– № 2 (62). – P. 69-82.
- Chusov V. V. Dva sposoba rascheta mer teorii nakaplivanija povrezhdenij [Two ways to calculate measures of damage accumulation theory] / V. V. Chusov , N. P. Aleksandrova // V sbornike: Nauka XXI veka: opyt proshlogo -vzgljad v budushhee: materiala II mezhdunarodnoj nauchno-prakticheskoj konferencii [In: Science of the XXI century: -vzglyad past experience into the future: the material of the II International Scientific and Practical Conference] – Omsk, SibADI, 2016 -P. 271-275. [in Russian]
- Aleksandrova N.P. Primenenie principa jekvivalentnosti deformacij k zadache rascheta mer teorii povrezhdennosti v uslovii plastichnosti asfal'tobetona [Application of the principle of equivalence of deformations to the problem of calculating measures of damage theory in the condition of plasticity of asphalt concrete]/ N. P. Aleksandrova, N. V. Kuzin, V. V. Chusov // Nauchnyj al'manah [Science Almanac]. – 2016. – № 7-1 (21). – P. 352-356. [in Russian]
