МЕТОД ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНОЙ ЧАСТОТЫ ПРОСТРАНСТВЕННОЙ МОДУЛЯЦИИ ДЛЯ ИЗМЕРЕНИЯ ТРЕХМЕРНОЙ ГЕОМЕТРИИ СЛОЖНОПРОФИЛЬНЫХ ОБЪЕКТОВ НА ОСНОВЕ ФАЗОВОЙ ТРИАНГУЛЯЦИИ
МЕТОД ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНОЙ ЧАСТОТЫ ПРОСТРАНСТВЕННОЙ МОДУЛЯЦИИ ДЛЯ ИЗМЕРЕНИЯ ТРЕХМЕРНОЙ ГЕОМЕТРИИ СЛОЖНОПРОФИЛЬНЫХ ОБЪЕКТОВ НА ОСНОВЕ ФАЗОВОЙ ТРИАНГУЛЯЦИИ
Научная статья
Двойнишников С.В.1, *, Куликов Д.В.2, Садбаков О.Ю.3, Бакакин Г.В.4, Павлов В.А.5, Меледин В.Г.6
1 ORСID: 0000-0002-0018-7675;
2 ORСID: 0000-0002-8516-5263;
3 ORСID: 0000-0001-6784-4273;
4 ORСID: 0000-0003-4712-7861;
5 ORСID: 0000-0003-3765-342X,
1, 2, 3, 4, 5, 6 Институт теплофизики им. С.С.Кутателадзе СО РАН, Новосибирск, Россия
* Корреспондирующий автор (dv.s[at]mail.ru)
Аннотация
В работе предложен метод определения оптимальной частоты пространственной модуляции для измерения трехмерной геометрии на основе структурированного освещения и фазовых шагов. Метод основан на построении амплитудно-частотной характеристики измерительного тракта по данным, полученным в процессе формирования световой засветки, реализующей код Грея. В результате данный метод измерения позволяет создать универсальный алгоритм управления измерительным комплексом, обеспечивающим измерение трехмерной геометрии методом фазовых шагов с наименьшей погрешностью при произвольных светорассеивающих свойствах поверхности.
Ключевые слова: фазовая триангуляция, трехмерные измерения, частота модуляции, структурированной освещение.
METHOD FOR DETERMINATION OF OPTIMUM FREQUENCY OF SPATIAL MODULATION FOR MEASUREMENT OF THREE-DIMENSIONAL GEOMETRY OF COMPLEX PROTECTIVE OBJECTS BASED ON PHASE TRIANGULATION
Research article
Dvoynishnikov S.V.1, *, Kulikov D.V.2, Sadbakov O.Yu.3, Bakakin G.V.4, Pavlov V.A.5, Meledin V.G.6
1 ORСID: 0000-0002-0018-7675;
2 ORСID: 0000-0002-8516-5263;
3 ORСID: 0000-0001-6784-4273;
4 ORСID: 0000-0003-4712-7861;
5 ORСID: 0000-0003-3765-342X,
1, 2, 3, 4, 5, 6Kutateladze Institute of Thermophysics, SB of RAS, Novosibirsk, Russia
*Corresponding author (dv.s[at]mail.ru)
Abstract
A method for determining the optimal frequency of spatial modulation for measuring three-dimensional geometry based on structured illumination and phase steps is proposed in the paper. The method is based on the construction of the amplitude-frequency characteristic of the measuring path according to data obtained during the light formation process, implementing the Gray code. As a result, this method of measurement makes it possible to develop a universal control algorithm for a measuring complex that provides the measurement of three-dimensional geometry by the method of phase steps with the smallest error for arbitrary light scattering properties of the surface.
Keywords: phase triangulation, three-dimensional measurements, modulation frequency, structured illumination.
Методы измерения геометрии сложных трехмерных объектов на основе триангуляционного принципа с использованием фазово-структурированного освещения активно развиваются и совершенствуются [1]. Простота их использования, низкая себестоимость комплектующих для создания измерительной системы и широкое применение в промышленных технологиях, научных исследованиях, медицине и строительстве подтверждает актуальность и востребованность исследований в области измерения трехмерной геометрии поверхности объектов методами оптической фазовой триангуляции и структурированного освещения.
В методе фазовой триангуляции погрешность определения фазы зависит от количества фазовых изображений N и относительной погрешности фотоприемника ![]() [2]:
[2]:
![]() (1)
(1)
Погрешность измерения координаты Z (глубины сцены), согласно [4] можно оценить, основываясь на геометрическом расположении оптических элементов в измерительной схеме:
![]() (2)
(2)
где p – период пространственной модуляции излучения, θ - угол триангуляции.
Из выражения (2) видно, что погрешность определения z координаты обратно пропорциональна частоте пространственной модуляции излучения. Отсюда получаем, что для минимизации погрешности измерения методом фазовых шагов необходимо обеспечить минимальный период пространственной модуляции оптического излучения.
Очевидно, что если уменьшать период пространственной модуляции излучения, то будет снижаться и диапазон измерения в методе фазовой триангуляции, так как фазовые значения могут однозначно восстанавливаться только в пределах периода. Чтобы увеличить диапазон измерения существует большое количество различных методов развертывания фазового поля, активно применяемых в интерферометрии. Известны алгоритмы, в которых для определения полной фазы на изображениях используют априорные данные об форме исследуемого объекта [3]. Существуют алгоритмы для восстановления полной фазы с помощью целочисленного анализа. Метод предусматривает формирование засветки объекта в виде серии фазовых изображений с различными кратными периодами пространственной модуляции излучения [4]. Наиболее перспективным для применения в триангуляционных измерениях с использованием структурированного освещения являются методы расширения диапазона измерения на основе комбинации метода фазовых шагов и метода бинарного кодирования пикселей [5], [6], [7]. Такой подход обеспечивает наилучшую точность измерений при проецировании наименьшего количества структурированных засветок.
На практике существуют ограничения на пространственное разрешение формируемого изображения оптической системой. Из-за ограниченной глубины резкости источника и приемника оптического излучения, аберрационных искажений оптических элементов измерительной системы невозможно получить абсолютно резкое изображение. Поэтому, необходимо определять частоту пространственной модуляции оптического излучения исходя из следующих условий. С одной стороны, частота излучения должна быть меньше, чем частота эквивалентного низкочастотного фильтра, которым является оптическая система измерителя. С другой стороны пространственная частота должна быть максимально большой для обеспечения минимальной погрешности измерения.
Как правило, данную проблему решают путем прямого выбора частоты пространственной модуляции при проектировании измерительной системы. Такой подход будет достаточно эффективен при измерении единообразных объектов с одинаковыми параметрами измерения. Однако в случае необходимости обеспечить высокоточные измерения сложнопрофильных объектов, свободно ориентированных в пространстве, такой подход может стать источником дополнительных ошибок измерения.
Известен метод оценки оптимальной пространственной модуляции на основе пространственно-частотного анализа наблюдаемого фотоприемником изображения [8]. Метод является достаточно трудоемким и при неудачном выборе структурного освещения может дать неточную оценку оптимальной частоты.
В данной работе предложен другой метод оценки оптимальной частоты пространственной модуляции. Метод заключается в выполнении 4-х шаговой процедуры измерения: на первом шаге на поверхности измеряемого объекта формируются изображения, кодирующие по горизонтальной координате рефлексивный бинарный код Грея [9]; на втором шаге определяют оптимальную частоту пространственной модуляции на основе полученных изображений; на третьем шаге формируют фазовые изображений с оптимальной частотой пространственной модуляции; на четвертом шаге вычисляют фазовый сдвиг и развертывают фазу на основе результатов измерения кодом Грея.
Оценка оптимальной частоты пространственной модуляции выполнялась следующим образом. Для каждой засветки в коде Грея вычисляется средняя наблюдаемая амплитуда источника излучения. Для этого на поверхность измеряемого объекта проецируют черно-белое изображение, соответствующее текущему шагу алгоритма и его негатив: изображение, где вместо черных полос формируются белые, а вместо белых - черные. Средняя амплитуда определяется по формуле:
![]() (3)
(3)
где ![]() – наблюдаемая яркость на изображении в точке с координатами (x,y) при проецировании засветки, кодирующей i-й шаг кода Грея,
– наблюдаемая яркость на изображении в точке с координатами (x,y) при проецировании засветки, кодирующей i-й шаг кода Грея, ![]() - наблюдаемая яркость на изображении в точке с координатами (x,y) при проецировании негатива засветки, кодирующей i-й шаг кода Грея,
- наблюдаемая яркость на изображении в точке с координатами (x,y) при проецировании негатива засветки, кодирующей i-й шаг кода Грея, ![]() – функция, определяющая видит ли фотоприемник в точке с координатами (x,y) сигнал от проектора:
– функция, определяющая видит ли фотоприемник в точке с координатами (x,y) сигнал от проектора:
![]() (4)
(4)
где N – порог, определяемый уровнем шумов на наблюдаемых изображениях.
Далее формируется функция зависимости средней амплитуды наблюдаемой засветки от частоты пространственной модуляции:
![]() (5)
(5)
где N – горизонтальное разрешение проектора, а период пространственной модуляции в коде Грея совпадает со степенью 2 порядкового номера засветки. Полученная зависимость A(F) является амплитудно-частотной характеристикой тракта источник-приемник оптического излучения измерительного комплекса.
Из полученной зависимости формируем регрессионную кривую и определяем частоту модуляции ![]() , при которой наблюдаемая амплитуда засветки будет соответствовать выражению:
, при которой наблюдаемая амплитуда засветки будет соответствовать выражению:
![]()
Параметр L определяет минимальный уровень амплитуды, превышающий амплитуду шума на регистрируемых фазовых изображениях. Его величина выбирается исходя из условий измерения и характеристик используемых оптико-электронных компонентов.
Выполнена экспериментальная демонстрация предложенного метода. В качестве источника структурированного излучения использован цифровой LED проектор, позволяющий формировать структурированное изображение с разрешением 104х768 пикселей. Наблюдаемые фотоприемником изображения обрабатывались в низком разрешении 320х240 пикселей для оценки качества предложенного алгоритма. На рис. 1 показаны зарегистрированные изображения структурированной засветки с кодом Грея на шаге 5 и 9.

Рис. 1 – Пример наблюдаемых фотоприемником структурированных засветок кодом Грея на шаге 5 (a) и 9 (б)
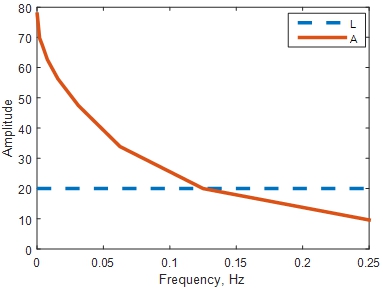
Рис. 2 – Полученная амплитудно-частотная характеристика тракта источник-приемник оптического излучения (А) и уровень
В результате выбрана частота пространственной модуляции 0.12 Гц., что соответствовало периоду гармонического сигнала на источнике излучения 52 пикселя (рис.3). На рис. 4 показана полученная зависимость наблюдаемой горизонтальной координаты проектора в зависимости от координат точки на фотоприемнике.

Рис. 3 – Пример фазового изображения с оптимальной частотой пространственной модуляции

Рис. 4 – Зависимость наблюдаемой горизонтальной координаты проектора в зависимости от координат точки на фотоприемнике
Видно, что в областях, попадавших в тень и не получавших освещение от источника структурированной засветки, результаты оказались в виде случайного шума. На рисунке 5 показан коэффициент достоверности измеренной координаты. Достоверность оценивалась, как максимальный наблюдаемый разброс амплитуды в точке. Из рис. 5 видно, что недостоверные точки, имеющий предельный уровень шума могут быть легко отброшены с помощью порогового фильтра, примененного к коэффициенту достоверности.

Рис. 5 – Коэффициент достоверности измеренной горизонтальной координаты проектора от координат точки на фотоприемнике, представленной на рис. 4
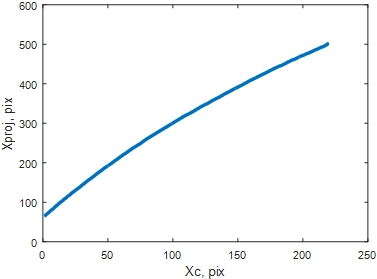
Рис. 6 – Срез изображения на рис.3 на высоте 150 пикселей
На рис. 6 представлен срез изображения на рис.4 на высоте 150 пикселей, демонстрирующий гладкий характер полученной кривой. Уровень шума составил около 0.5% от измерительного диапазона, что является очень высоким, учитывая низкое качество используемых оптико-электронных элементов измерителя и намеренно заниженное разрешение анализируемых изображений, наблюдаемых на фотоприемниках. Уровень шума оценивался по среднеквадратичному отклонению значений на полученной кривой от усредненного значения после сглаживания фильтром скользящего среднего.
В работе предложен метод определения оптимальной частоты пространственной модуляции при измерении трехмерной геометрии сложнопрофильных объектов методом фазовой триангуляции. Предложенный подход позволяет использовать оптимальную частоту пространственной модуляции оптического источника при измерениях трехмерной геометрии методом фазовых шагов и бинарного кода Грея. Метод основан на построении АЧХ измерительного тракта по данных, полученных в процессе формирования световой засветки, реализующей код Грея. В результате данный метод измерения позволяет создать универсальный алгоритм управления измерительным комплексом, обеспечивающим измерение трехмерной геометрии методом фазовых шагов с наименьшей погрешностью при произвольных светорассеивающих свойствах поверхности.
| Финансирование Работа выполнена при поддержке Российского фонда фундаментальных исследований, грант №18-08-00910. | Funding The work was supported by the Russian Foundation for Basic Research, grant No. 18-08-00910. |
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Gorthi S.S. Fringe projection techniques: Whither we are? / S.S. Gorthi, P. Rastogi // Optics and Lasers in Engineering 48 (2010). – p. 133-140.
- Dvoynishnikov S.V. Optoelectronic method of contactless reconstruction of the surface profile of complexly shaped three-dimensional objects / S.V. Dvoynishnikov. D.V.Kulikov, V.G. Meledin // Measurement Techniques. 2010, 53(6). –P. 648-656.
- Guzhov V.I. Practical aspects of phase measurement in interferometry // Avtometria, Issue 5 (1995). – p. 25-31.
- Guzhov V.I. Accuracy analysis of determination of phase total difference in integer interferometers / V.I. Guzhov, Yu.N. Solodkin // Avtometria, Issue 6 (1992). – p. 24-30.
- Inokuchi S. Range-imaging system for 3-D object recognition / S. Inokuchi, K. Sato // Proceeding of 7th International Conference Pattern Recognition, Montreal, Canada, 1984. - p. 806–808.
- Stahs T. Fast and versatile range data acquisition / T. Stahs, F. Wahl // IEEE/RSJ International Conference Intelligent Robots and Systems, Raleigh, NC, July 1992. - pp. 1169–1174.
- Dvoinishnikov S.V. An Optoelectronic Method of Contactless Measurement of the Profile of the Surface of Large Complexly Shaped Objects / Dvoinishnikov S.V., Anikin Y.A., Kabardin I.K. and others // Measurement Techniques. 2016, 59(1). - p. 21-27.
- Dvoinishnikov S.V. Estimation of Optimal Frequency of Spatial Modulation of the Radiation of 3D Measurements / S.V. Dvoinishnikov, V.G. Meledin, V.G. Glavnyi and others // Measurement Techniques. 2015, 58(5). – p. 506-511.
- Goddyn L. Binary gray codes with long bit runs. The Electronic Journal of Combinatorics. 2003. 10(1), 10 p.
