МЕТОД АНАЛИЗА РАЗМЕРНОСТЕЙ В ГИДРАВЛИЧЕСКИХ ИССЛЕДОВАНИЯХ СТРУЙНОГО РАЗБАВЛЕНИЯ

Зверева В.А.¹, Гулякин А.В.²

¹Доцент,кандидат технических наук, Дальневосточный федеральный университет;

 ²Студент,Дальневосточный федеральный университет

МЕТОД АНАЛИЗА РАЗМЕРНОСТЕЙ В ГИДРАВЛИЧЕСКИХ ИССЛЕДОВАНИЯХ СТРУЙНОГО РАЗБАВЛЕНИЯ

Аннотация

В работе представлены результаты использования метода анализа размерностей в исследованиях струйного разбавления при выпуске сточных вод в мелкие водоёмы.

В процессе исследования получен критерий для определения возможной схемы растекания струи сточной жидкости в ограниченном (мелком) по глубине водоёме, влияющей на степень струйного разбавления.

Ключевые слова: разбавление, струя, размерность, моделирование, критерий.

Zvereva V.A.¹, Gulyakin A.V.²

¹Docent, PhD in water supply and water sewage, associate professor, Far Eastern Federal University (FEFU);

²Student, Far Eastern Federal University (FEFU)

THE METHOD OF DIMENSIONAL ANALYSIS IN HYDRAULIC STUDIES OF JET DILUTIONS

Abstract

There were presented result of  using of method analysis of dimensions in the research process of jet dilutions with release wastewater into the small pound.

During the research a criterion for determining the possible outline of spreading the liquid waste stream in a limited (small) reservoir depth which affects the degree of dilution of the jet.

Keywords: dilutions, stream, dimensional, modeling, criteria.

Исследования гидравлических процессов сопровождаются моделированием, которое бывает двух видов: математическое и физическое.

Система уравнений, описывающих определённый физический процесс, представляет собой математическую модель. Решение этих уравнений и есть математическое моделирование.

При физическом моделировании гидравлического процесса создаётся модель сооружения, устройства или гидравлической машины, уменьшенная в масштабе.

Для полного гидродинамического подобия потоков жидкости на модели и натуре необходимо соблюдение геометрического, кинематического и динамического подобия.

Геометрическое подобие предполагает постоянное соотношение между соответствующими линейными размерами натуры и модели. Кинематическое подобие предполагает подобие полей скоростей и ускорений в натуре и на модели. Условием гидродинамического подобия является равенство на модели и в натуре отношений всех сил, действующих в потоке (тяжести, трения, давления, инерции и др.) Подобие сил определяют с помощью критериев подобия.

Подобие всех сил практически невозможно, поэтому критерии подобия устанавливают для частных случаев, учитывающих преобладающую силу из всех действующих сил.

Методы подобия и методы размерностей находятся в тесной связи между собой.

Метод анализа размерностей может рассматриваться в качестве одного из дополнительных методов исследований и предполагает всестороннее знание изучаемого физического процесса.

Согласно метода анализа размерностей в любом уравнении размерности (единицы измерения) выражений слева и справа должны совпадать. Тогда формула верна с точностью до безразмерного множителя. Данный метод основан на рассмотрении размерностей физических величин, существенно влияющих на изучаемое явление.

Уравнение, выражающее связь физических величин, должно оставаться справедливым при любом изменении единиц измерения, входящих в уравнение величин, то есть должно иметь место равенство размерностей величин в левой и правой частях уравнении.

Известно, что в международной системе единиц (СИ), единицей измерения длины (L) является метр, м; массы (m) – килограмм, кг; времени (t) – секунда, с; силы (F) – ньютон, H.

Если для исследуемого процесса установлено, с какими величинами может быть связана искомая величина, но вид этой связи неизвестен, для её нахождения составляют уравнение размерностей, в котором в левой части будет стоять символ искомой величины со своим показателем размерности, а в правой – произведение символов величин, от которых искомая величина зависит, но с неизвестными показателями размерности.Задача нахождения связи между физическими величинами сводится в этом случае к отысканию значений соответствующих показателей размерности.

В качестве примера рассмотрим известное выражение для определения массовой силы:

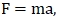    (1.1)

где F – сила, Н; m – масса, кг; a–ускорение, м/с².

С учётом размерностей эта формула в системе СИ должна быть переписана в виде:

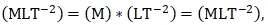   (1.2)

Как видно, размерность левой и правой частей совпадает, следовательно, формула не противоречит физической сущности явления.

Наиболее важное значение анализ размерностей приобретает в связи с возможностью его использования для написания формул. Рассмотрим пример получения всем известной формулы Торричелли. Известно, что скорость падения тела зависит от высоты расположения тела h и ускорения силы тяжести g, т.е. функциональна:

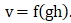     (1.3)

На основании метода анализа размерности зависимость (1.3) может быть  записана в виде

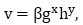    (1.4)

где: β – неизвестный, постоянный, безразмерный коэффициент; x, y – неизвестные численные показатели степени.

Учитывая размерности входящих в эту формулу величин

 

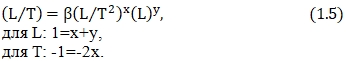
Решая эту систему уравнений, найдём, что x=y=1/2. Подставляя полученные значения в (1.4), определим

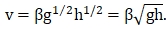    (1.6)

Значение β было определено из опыта и оно оказалось равным ≈ 1,41.

В результате

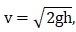     (1.7)

т.е  получена общеизвестная формула механики, формула Торричелли.

В ДВГТУ на кафедре гидравлики, водоснабжения и водоотведения изучались вопросы разбавления сточных вод, сбрасываемых в водоёмы. Известно, что процесс разбавления состоит из двух этапов – струйного (начального), и диффузионного (основного). В лаборатории гидравлики проводились  экспериментальные исследования струйного разбавления при выпуске сточных вод в мелкие, ограниченные по глубине, акватории, которые в отличии от больших водоёмов не обладают достаточной возможностью вовлекать струю сточной жидкости для разбавления чистых объёмов воды.

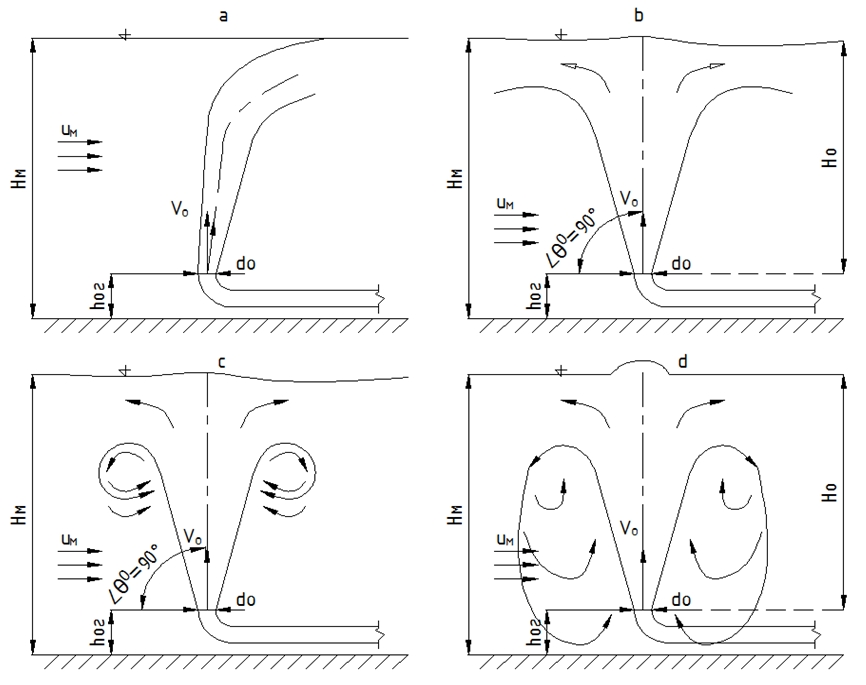
Исследования на физической модели показали, что возможны четыре схемы растекания струи сточной жидкости в ограниченном по глубине водоёме (рисунок 1):

1. струя в сносящем потоке;
2. струя, бьющая в препятствие без образования циркуляционных зон;
3. струя, бьющая в препятствие с образованием циркуляционных зон;
4. струя, бьющая в препятствие с циркуляционными зонами, распространяющимися практически на всю глубину водоёма.

На степень струйного разбавления сточных вод чистыми водами влияют многие факторы, сочетания которых формируют схемы растекания.

Основная задача исследований заключалась в получении зависимости и критериев для определения схемы растекания струи сточной жидкости в мелком водоёме.

Распространение струи по схеме (а) было названо свободным. В схемах (b, c, d) – растекание струи происходит в стеснённых, ограниченных по глубине,  условиях. Под ограничением в данном случае понимают наличие на пути движения струи свободной поверхности, препятствующей дальнейшему распространению вертикальной струи. За основной признак нестеснённого растекания была принята достаточность количества жидкости, принимающая струю водоёма (сносящего потока), необходимой для обеспечения присоединения секундной массы струи. Характерным признаком струи при недостаточном для вовлечения в струю расхода сносящего потока является образование циркуляционных зон.

Рис. 1 – Возможные схемы растекания струи в мелком водоёме

Исследования распространения струи сточной жидкости в мелком водоёме показали, что на форму растекания струи влияют: глубина водоёма в районе выпуска (H_м), средняя скорость потока в районе выпуска (U_м), средняя скорость струи сточной жидкости на выходе из оголовка выпуска (V_o), плотность среды, принимающей сточную жидкость (ρ_м), плотность сточной жидкости на выходе из оголовка выпуска (ρ_o), диаметр оголовка (d_o), высота оголовка над дном (h_ог), вязкость сточной жидкости (μ_о), вязкость  воды принимающего водоёма (μ_м) и угол наклона оголовка выпуска к горизонту (θ).

Анализируя схемы растекания струи сточной жидкости можно считать, что при всех равных условиях (ρ_о=const; ρ_м=const и т.д.), струя может перейти от схемы растекания (а) к схеме (b) как только изменится скорость сносящего потока (U_м). Вместе с тем, изменение одной из величин, влияющих на схему растекания (h_ог; H_м; ρ_o; ρ_м и т.д.) потребует соответственно нового значения скорости U_м, для перехода струи от одной схемы растекания к другой.

Предположим, что все величины, влияющие на растекание струи, связаны между собой функциональной зависимостью

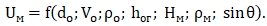    (1.8)

Обозначим H_м-h_ог=H_o.

Представим U_м в виде степенного комплекса величин d_o, ρ_o, H_o, ρ_м, V_o, sinθ:

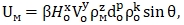     (1.9)

где: β – коэффициент пропорциональности; x, y, z, p, k – неизвестные показатели степени.

Зависимости  (1.9) в символах размерностей принимает вид

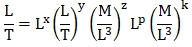     (1.10)

или

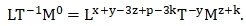    (1.11)

Приравниваем показатели степеней при одноимённых размерностях в правой и левой частях уравнения (1.11)

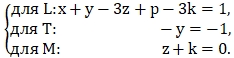     (1.12)

Получим решение системы (1.12) в следующем виде

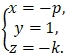      (1.13)

Подставляя значения x, y, zв зависимость (1.9), получим

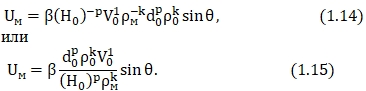
Из уравнения (1.15) выразим β

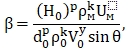    (1.16)

Составим зависимость между основными параметрами в другом виде, например:

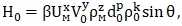    (1.17)

Используя анализ размерностей, можно доказать, что из зависимости (1.17) вновь получаем:

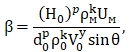     (1.18)

В теории турбулентных струй при выводе ряда закономерностей успешно используется теорема импульсов. Если в уравнениях  (1.16) и (1.18) принять p=1 k=1; y=1, то безразмерная обобщённая характеристика β представляет собой отношение удельного импульса сносящего потока к удельному импульсу струи, что физически является вполне оправданным.

Тогда

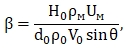     (1.19)

Для вертикальной струи (θ=90⁰):

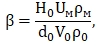      (1.20)

или

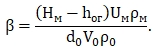     (1.21)

При ρ₀=ρ_м

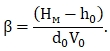    (1.22)

Полученный параметр β отражает влияние свободной поверхности и мощности сносящегося потока на структурную схему растекания струи.

Дальнейшие экспериментальные исследования показали, что параметр β при распространении струи в среде той же плотности имеет критические значения β_кр.в = 1,15 – верхнее критическое значение; β_кр.н = 0,6 – нижнее критическое значение.

Таким образом, используя уравнения (1.22) и критерии β_кр можно определить схему растекания струи сточной жидкости в мелком водоёме:  при β>1,15 имеет место свободное растекание струи в водоёме, обеспечивающее максимальную степень начального разбавления (схема а). Переход струи от свободного растекания к радиальному происходит при β = 1,15 (схема b). Если β<1,15, но >0,6 струя распространяется по схеме b или c. При β≤0,6 струя распространяется по схеме d, т.е. самой неблагоприятной для процесса разбавления сбрасываемых загрязнённых жидкостей в мелкий водоём.

На практике сточные воды имеют меньшую плотность, чем плотность жидкости принимающего водоёма. Чтобы обеспечить условие ρ₀<ρ_м, на модели жидкость, имитирующая сточные воды предварительно нагревалась до заданной температуры.

Результаты экспериментов (при ρ₀<ρ_м) позволили выразить аналитически параметр β, отделяющий схемы растекания струи, по зависимости

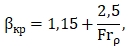    (1.23)

где: Fr_ρ -  плотностное число Фруда.

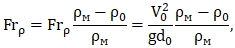    (1.24)

Итак, если параметр β, определяемый по уравнению (1.21) > β_кр (1.23), то струя расширяется по схеме (а) – струя в сносящем потоке. Если β<β_кр – то имеем струю, распространяющуюся по схеме (b). Чем меньше β, тем ниже эффект начального разбавления, за счёт образования циркуляционных зон, а значит присоединения к струе сточной жидкости загрязнённых объёмов воды.