МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ВИТКОВЫХ КОРОТКИХ ЗАМЫКАНИЙ В ОБМОТКЕ СТАТОРА АВТОНОМНОГО АСИНХРОННОГО ГЕНЕРАТОРА

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ВИТКОВЫХ КОРОТКИХ ЗАМЫКАНИЙ В ОБМОТКЕ СТАТОРА АВТОНОМНОГО АСИНХРОННОГО ГЕНЕРАТОРА

Научная статья

Соболь А.Н.^1, *, Андреева А.А.²

^{1, 2} ФГБОУ ВО Кубанский государственный аграрный университет имени И.Т. Трубилина, Краснодар, Россия

* Корреспондирующий автор (asob2010[at]mail.ru)

Аннотация

В статье рассматривается построение математической модели симметричных трехфазных витковых коротких замыканий в обмотке статора автономного асинхронного генератора, являющихся предельным случаем размагничивания короткозамкнутых контуров обмотки. Адекватность полученной модели подтверждена экспериментально. С помощью полученной модели появляется возможность достоверно рассчитать токи, а также другие возможные характеристики ААГ при витковых замыкания в статорной обмотке, необходимые для построения защитных устройств.

Ключевые слова: асинхронный генератора, модель, витковые замыкания.

MATHEMATICAL MODELING OF TURN-TO-TURN SHORT CIRCUITS IN STATOR WINDING OF AUTONOMOUS ASYNCHRONOUS GENERATOR

Research article

Sobol A.N.^1, *, Andreeva A.A.²

^{1, 2} FSBEI of HE Kuban State Agrarian University named after I.T. Trubilin, Krasnodar, Russia

* Corresponding author (asob2010[at]mail.ru)

Abstract

The article considers the construction of the mathematical model of symmetric three-phase turn-to-turn short circuits in the stator winding of an autonomous asynchronous generator, which is the limiting case of demagnetization of turn-to-turn short circuit windings. The adequacy of the obtained model is approved experimentally. The obtained model enables us to reliably calculate the currents, as well as other possible characteristics of the AAG during a short circuit in the stator winding, which is necessary for the construction of protective devices.

Keywords: asynchronous generator, model, coil circuits.

Ведение

В наше время широкое распространение получили автономные асинхронные генераторы с емкостным самовозбуждением. Как показано в обзорах [10] и [12] генераторы нашли применение в электроснабжении предприятий, а та также для личных нужд в качестве альтернативных источников энергии.

Тем не менее в процессе их эксплуатации возникают различные трудности. Это обусловлено отсутствием чувствительных защит генераторов.

Большая доля всех отказов асинхронных машин (более 90 %), согласно данным [7] и [11], приходится на различные виды повреждений обмотки статора, в том числе на витковые короткие замыкания. Тем не менее в [2] говориться о том, что существует мнение о ненужности защиты генератора поскольку при витковых коротких замыканиях в статорной обмотке он теряет возбуждение. Однако, в результате проведенных опытных исследований доказано, что в случае наличия небольшого (3 – 5 %) количества короткозамкнутых витков обмотки, генератор продолжает длительно работать, имея при этом замкнутые витки в обмотке. В результате происходит снижение надежности электроустановки, использующей асинхронный генератор, как источника электроснабжения.

В процессе разработки защиты генератора от витковых коротких замыканий, как показано в [4], необходимо знать информационные признаки данного вида повреждений и их специфику.

В процессе выявления данных информационных параметров, как показано в [12] и [13], особая роль отводится математическому моделированию. Необходимо разработать модель, позволяющую изучить электромагнитные процессы, протекающие при этом в генераторе, в частности, диапазон изменения фазных токов и напряжений, а также спрогнозировать развитие данных процессов. Кроме того, математическая модель позволяет дополнить физический эксперимент, что, несомненно, является ценным для изучения аварийных режимов работы генератора. Согласно [9] данный факт позволяет установить целесообразность использования различных устройств защиты.

Методы и принципы исследования

Электромагнитное воздействие короткозамкнутого контура в обмотке статора выражается в размагничивании генератора. При этом магнитный поток в области данного контура уменьшается. В связи с этим целесообразно рассмотреть модель с наличием короткозамкнутых контуров сразу в трех фазах статорной обмотки, так как данный вид повреждений является предельным случаем такого вида размагничивания.

Кроме того, построение данной симметричной математической модели облегчается тем, что в данном случае применимы допущения, описанные в [6] и [12] и являющиеся традиционными для симметричных машин. Среди таких допущений можно выделить электрическую, магнитную и, кроме того, пространственную симметрию машины. Принимаем, что поверхности ротора и статора генератора имеют цилиндрическую форму. Значение магнитной проницаемости стальных участков генератора равно бесконечности. Распределение магнитодвижущей силы в зазоре имеет гармонический характер (данные обмотки носят название «синусных»). Также считаем, что вращающееся поле машины имеет круговую форму, число параллельных ветвей статорной обмотки равно единице, а сама обмотка выполнена одним элементарным проводником.

Для получения нашей модели необходимо вначале ввести понятие относительного числа короткозамкнутых витков.

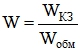   (1)

где  – количество замкнувшихся витков, – общее количество витков в фазе.

Составим систему дифференциальных уравнений в системе α-β координат, как наиболее удобную для решения с помощью ЭВМ, учитывая внешнюю емкость конденсаторной батареи (с), а также нагрузку (сопротивление ). Система координат представлена на рисунке 1.

Предварительно введем, как описано в [7], обозначения основных параметров в относительных величинах. Для этого принимаем следующие основные базовые величины, к которым относятся амплитудные номинальные значения фазного тока и напряжения, номинальное значение угловой частоты, а также номинальное значение момента

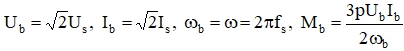    (2) где  – номинальное напряжение и ток статора соответственно,  – частота тока, p – число пар полюсов.  

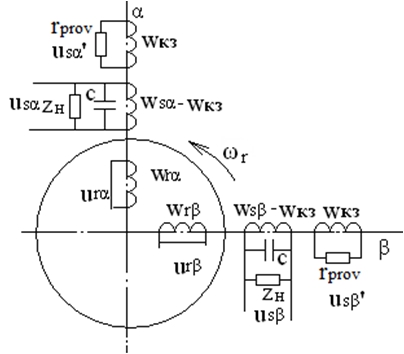
Рис. 1 – Пространственная модель ААГ в неподвижной α-β системе координат для исследования симметричных витковых коротких замыканий

  Также согласно [3] принимаем базовые величины сопротивления, индуктивности, емкости, а также времени соответственно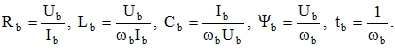     (3)

Ток статора и нагрузки, сопротивления статорной и роторной обмоток, индуктивность цепи нагрузки в относительных величинах определяются следующим образом

    (4)

где  – реальные величины напряжения, тока статора, тока нагрузки, потокосцепления и индуктивности нагрузки,  – соответственно величины активных сопротивлений статора и ротора.

Кроме того, введем относительные величины электромагнитного момента, а также вращающего моментов приводного двигателя

    (5)

где  – электромагнитный момент асинхронного генератора,  – вращающий момент приводного двигателя.

Аналогичным образом запишем следующие безразмерные параметры

    (6)

где  – индуктивности статора, ротора, а также взаимная индуктивность соответственно, J – сумма моментов ротора, а также вращающего генератор механизма.

Введем также величины

    (7)

где t – время, – угловая скорость ротора, C – емкость цепи возбуждения.

Определяем безразмерные коэффициенты следующим образом

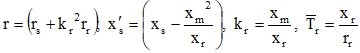    (8) И, на конец, для записи системы дифференциальных уравнений вводим коэффициенты.    (9)

где W – число замкнувшихся витков в соотношении с числом витков в фазе,  – сопротивление образовавшегося короткозамкнутого контура.

Итоговая система уравнений, включающая ток в короткозамкнутом контуре  будет иметь следующий вид

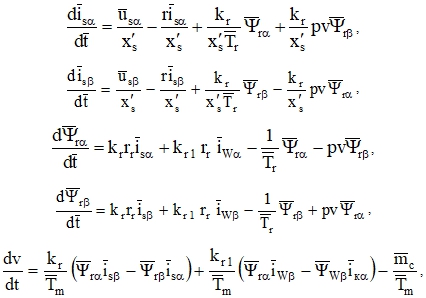
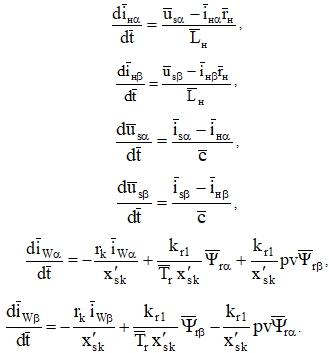
Для решения данной системы использовался пакет MathCAD.

Чтобы модель была адекватна, необходимо сравнить ее выходные данные данными, как описано в [8], с полученными в ходе опытных испытаний реальной установки с генератором. Опытный стенд включал в себя самовозбуждающийся генератор, выполненный на основе электрического двигателя марки 4A100S4У3.

Основные результаты

Ток в фазе генератора с наличием короткозамкнутых витков и собственно ток короткозамкнутой части обмотки показаны на рисунках 2 и 3. Зависимости получены двумя способами, а именно решением уравнений в MathCAD и осциллографированием реальных токов генератора.

Рис. 2 – Ток в фазе генератора

Рис. 3 – Ток в короткозамкнутой части обмотки

 

На основании этих данных можно утверждать, что в случае симметричного виткового короткого замыкания происходит уменьшение тока поврежденной фазы. Ток короткозамкнутого контура превышает в несколько раз номинальный ток генератора.

При этом видно, что полученная математическая модель хорошо согласуется с экспериментальными данными. Отличие полученных зависимостей составляет величины 3 – 4 %. Таким образом, можно говорить об адекватности модели.

Заключение

С помощью дифференциальных уравнений нам удалось получить работающую модель. С ее помощью появляется возможность изучить происходящие при повреждении обмотки в генераторе процессы.

Благодаря разработанной модели было установлено, что в случае наличия сразу во всех трех фазах генератора 3 % короткозамкнутых витков происходит изменение токов в фазах, а именно их уменьшение в 1,2 раз. Также удалось получить кривую тока короткого замыкания. Его значение шестикратно превышает номинальный ток в фазах генератора. При этом генератор продолжает функционировать, несмотря на то, что его обмотка повреждена.

Разработанная модель удовлетворяет условиям адекватности. В частности, это подтверждается экспериментально путем сравнения кривых токов, которые получены в результате моделирования с осциллограммами, полученными опытным путем на стенде. Разница значений токов при этом составляет всего 3 – 5 %.

Данная модель с большой долей достоверности позволяет получить значения токов и других возможных электромеханических характеристик самовозбуждающегося генератора при симметричном замыкании витков его статорной обмотки. Данные характеристики могут быть использованы для разработки соответствующих защитных устройств.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Баракин Н. С. Асинхронный генератор с автотрансформаторной обмоткой статора / Н. С. Баракин, А. Н. Соболь, А. А. Кумейко // Сельский механизатор. ‑ 2018. ‑ № 7-8. ‑ С. 48 – 49.
2. Богдан А. В. Информационные признаки повреждения обмотки статора для построения релейной защиты автономного асинхронного генератора / А. В. Богдан, А. Н. Соболь // Известия вузов. Электромеханика. ‑ 2017. – № 6. ‑ С. 72-76.
3. Богдан А. В. Математическая модель самовозбуждения автономного асинхронного генератора / А. В. Богдан, А. Н. Соболь // Известия вузов. Электромеханика. ‑ 2012. – № 2. ‑ С. 47-50.
4. Богдан А. В. Обнаружение виткового замыкания в обмотке статора асинхронного генератора / А. В. Богдан, А. Н. Соболь, Н. С. Баракин // Сельский механизатор. ‑ 2018. – № 7-8. ‑ С. 44 – 45.
5. Герман-Галкин, С. Г. Компьютерное моделирование полупроводниковых систем MATLAB0 / С. Г. Герман-Галкин. – М.: Корона принт, 2001. – 320 с.
6. Копылов И. П. Электрические машины: учебник / И. П. Копылов. – М.: Юрайт, 2015. – 630 с
7. Кулаковский В. Б. Работа изоляции в генераторах: Возникновение и методы выявления дефектов / В. Б. Кулаковский. – М.: Энергоиздат, 1981. – 256 с.
8. Соболь А. Н. Диагностика повреждений в обмотке статора автономного асинхронного генератора / А. Н. Соболь // Инновации в сельском хозяйстве. – 2016. ‑ № 2. ‑ С. 225-228.
9. Пат. 66127 U1 Российская Федерация, МПК H 02 K 11 00, H 02 H 7 08. Устройство для дифференциальной защиты асинхронного генератора / Соболь А. Н.; заявитель и патентообладатель Федеральное государственное бюджетное образовательное учреждение высшего образования «Кубанский государственный аграрный университет. ‑ № 2006147115/22; заявл. 27.12.06; опубл. 27.08.07, Бюл. № 24. – 4 с.
10. Торопцев Н. Д. Области применения асинхронных генераторов / Н. Д. Торопцев // Энергетик. – 2004. – № 3. – С. 31 – 34.
11. Eftekhari M. Online Detection of Induction Motor’s Stator Winding Short-Circuit Faults / M. Eftekhari, M. Moallem, S. Sadri, and M.-F. Hsieh // IEEE Systems Journal. – 2013. ‑ Vol. PP. ‑ No. 99. ‑ P. 1 – 11.
12. Rasel Sarkar Mathematical modelling and simulation of induction generator based wind turbine in Matlab / Simulink / Md. Rasel Sarkar, Sabariah Julai, Chong Wen Tong, Ong Zhi Chao and Mahmudur Rahman // ARPN Journal of Engineering and Applied Sciences. – 2015. ‑ Vol. 10. ‑ No. 22. ‑ P. 17276 – 17280.
13. Jain S.K. Transient performance of three-phase self-excitedinduction generator during balancedand unbalanced faults / S.K. Jain, J.D. Sharma and S.P. Singh // IEE Proc.-Gener. Trans. Distrib. – 2002. ‑ Vol. 149. ‑ Vol. 149. ‑ No.1. ‑ P. 50 – 57.

Список литературы на английском языке / References in English

1. Barakin N. S. Asinhronnyj generator s avtotransformatornoj obmotkoj statora [Asynchronous generator with autotransformer stator winding] / N. S. Barakin, A. N. Sobol', A. A. Kumejko // Sel'skij mekhanizator [Rural machine operator]. ‑ 2018. ‑ № 7-8. ‑ P. 48 – 49. [in Russian]
2. Bogdan A. V. Informacionnye priznaki povrezhdeniya obmotki statora dlya postroeniya relejnoj zashchity avtonomnogo asinhronnogo generator [Information signs of stator winding damage for building relay protection of an autonomous asynchronous generator] / A. V. Bogdan, A. N. Sobol' // Izvestiya vuzov. Elektromekhanika [University News. Electromechanics]. ‑ 2017. – № 6. ‑ P. 72-76. [in Russian]
3. Bogdan A. V. Matematicheskaya model' samovozbuzhdeniya avtonomnogo asinhronnogo generator [A mathematical model of self-excitation of an autonomous asynchronous generator] / A. V. Bogdan, A. N. Sobol' // Izvestiya vuzov. Elektromekhanika [University News. Electromechanics]. ‑ 2012. ‑ № 2. ‑ P. 47-50. [in Russian]
4. Bogdan A. V. Obnaruzhenie vitkovogo zamykaniya v obmotke statora asinhronnogo generator [Detection of a short circuit in the stator winding of an asynchronous generator] / A. V. Bogdan, A. N. Sobol', N. S. Barakin // Sel'skij mekhanizator [Rural machine operator]. ‑ 2018. ‑ № 7-8. ‑ P. 44 ‑ 45. [in Russian]
5. German-Galkin, S. G. Komp'yuternoe modelirovanie poluprovodnikovyh sistem MATLAB 6.0 [Computer simulation of semiconductor systems MATLAB 6.0] / S. G. German-Galkin. – M.: Korona print, 2001. – 320 p. [in Russian]
6. Kopylov I. P. Elektricheskie mashiny: uchebnik [Electric machines: a tutorial] / I. P. Kopylov. – M.: YUrajt, 2015. – 630 p. [in Russian]
7. Kulakovskij V. B. Rabota izolyacii v generatorah: Vozniknovenie i metody vyyavleniya defektov [Insulation Operation in Generators: The Occurrence and Methods of Detecting Defects] / V. B. Kulakovskij. – M.: Energoizdat, 1981. – 256 p. [in Russian]
8. Sobol' A. N. Diagnostika povrezhdenij v obmotke statora avtonomnogo asinhronnogo generator [Diagnosis of damage in the stator winding of an autonomous asynchronous generator] / A. N. Sobol' // Innovacii v sel'skom hozyajstve [Agricultural Innovation]. ‑ 2016. ‑ № 2. ‑ P. 225-228. [in Russian]
9. 66127 U1 Rossijskaya Federaciya, MPK H 02 K 11 00, H 02 H 7 08. Ustrojstvo dlya differencial'noj zashchity asinhronnogo generatora [Device for differential protection of an asynchronous generator] / Sobol' A. N.; the applicant and the patentee Federal State Budgetary Educational Institution of Higher Education “Kuban State Agrarian University. ‑ № 2006147115/22; appl. 27.12.06; publ. 27.08.07, Bul. Number 24. ‑ 4 p.
10. Toropcev N. D. Oblasti primeneniya asinhronnyh generatorov [Applications for Asynchronous Generators] / N. D. Toropcev // Energetik [Power engineer]. ‑ 2004. ‑ № 3. ‑ P. 31 – 34.
11. Eftekhari M. Online Detection of Induction Motor’s Stator Winding Short-Circuit Faults / M. Eftekhari, M. Moallem, S. Sadri, and M.-F. Hsieh // IEEE Systems Journal. – 2013. ‑ Vol. PP. ‑ No. 99. ‑ P. 1 – 11.
12. Rasel Sarkar Mathematical modelling and simulation of induction generator based wind turbine in Matlab / Simulink / Md. Rasel Sarkar, Sabariah Julai, Chong Wen Tong, Ong Zhi Chao and Mahmudur Rahman // ARPN Journal of Engineering and Applied Sciences. – 2015. ‑ Vol. 10. ‑ No. 22. ‑ P. 17276 – 17280.
13. Jain S.K. Transient performance of three-phase self-excitedinduction generator during balancedand unbalanced faults / S.K. Jain, J.D. Sharma and S.P. Singh // IEE Proc.-Gener. Trans. Distrib. – 2002. ‑ Vol. 149. ‑ Vol. 149. ‑ No.1. ‑ P. 50 – 57.