МАТЕМАТИЧЕСКАЯ МОДЕЛЬ УПРУГИХ КОЛЕБАНИЙ ТРУБОПРОВОДА ПРИ УДАРНОМ ВОЗДЕЙСТВИИ
Федотов А.А.
Соискатель, Омский государственный университет путей сообщения
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ УПРУГИХ КОЛЕБАНИЙ ТРУБОПРОВОДА ПРИ УДАРНОМ ВОЗДЕЙСТВИИ
Работа выполнена при финансовой поддержке РФФИ (грант № 17-08-01560)
Аннотация
Представлена модель упругих колебаний, фиксируемых на поверхности трубопровода в результате ударного точечного воздействия. Проведена оценка адекватности полученного аналитического выражения путем сравнения характеристик теоретического сигнала с эмпирическим, полученным на макете трубопровода и на действующем участке трубопровода протяженностью 200м. Результаты моделирования позволили сделать вывод о высокой достоверности модели в задаче аналитического описания колебаний трубопровода при работе в ближней зоне и необходимости введения дополнительных параметров в полученное выражение для описания упругих колебаний в протяженных действующих трубопроводах.
Ключевые слова: модель колебаний, упругие колебания, трубопровод, ударное воздействие, виброакустический способ контроля, стержневая теория.
Fedotov A.A.
Postgraduate Student, Omsk State Transport University
MATHEMATICAL MODEL OF ELASTIC VIBRATION OF A PIPELINE UNDER IMPACT EFFECT
Abstract
The article presents a model of elastic oscillations fixed on the surface of a pipeline as a result of the point impact effect. We conducted the evaluation of the adequacy of the obtained analytical expression by means of comparing the characteristics of the theoretical signal with the empirical one, obtained on the pipeline layout and on the operating section of the pipeline with a length of 200 m. The results of the simulation allowed us to conclude that the model is highly reliable in the problem of analytical description of pipeline oscillations, in particular, when operating in the near zone and when there is the need to introduce additional parameters into the expression obtained to describe elastic oscillations in long operating pipelines.
Keywords: oscillation model, elastic oscillations, pipeline, impact effect, vibro-acoustic control method, bar theory.
В работах [1,2] обозначена проблема обеспечения безопасности линейной части магистральных трубопроводов, выраженная в отсутствии эффективных решений по автоматическому обнаружению несанкционированной деятельности. Представлен активный виброакустический способ контроля [2,3], позволяющий предотвращать совершение хищений нефтепродуктов посредством контроля состояния структуры оболочки трубопровода и окружающей его среды.
Контроль состояния трубопровода обеспечивается формированием в его оболочке периодической последовательности импульсов упругих колебаний генератором, установленным на поверхности трубы. При возникновении переизлучения акустической энергии (шурф, установка предмета) фиксируется изменение параметров виброакустического сигнала.
Теоретические сведения о формировании виброакустических сигналов в результате воздействия ударника с трубопроводом не приведены. В данной статье предлагается описать аналитически модель импульса упругих колебаний, возникающего в трубопроводе при точечном воздействии на его оболочке, что позволит в дальнейшем моделировать работу системы контроля.
Представляется возможным описать аналитически поперечные колебания трубопровода, если взять за основу модель колебания стержня [4]. Участок трубопровода можно представить в качестве стержня с различными типами закрепления, в зависимости от вида трубопровода и разновидности опор. Опоры могут представлять из себя упругое основание, либо основание с пружинами для компенсации вибраций и предотвращения разрушения трубы [5]. Наиболее близким условием закрепления для модели следует считать свободное.
Реализуем моделирование виброакустического сигнала, фиксируемого в лабораторных условиях на поверхности трубы без жидкости длиной пять метров с диаметром 0,038 м, покоящейся свободно на двух металлических опорах.
При разложении колебаний стержня по модам функция поперечных колебаниях имеет вид [4]:
![]()
Постоянные ![]() определяются в каждом случае, в зависимости от условий закрепления стержня. Всегда имеется возможность записать такие концевые условия, которым соответствуют определенные величины
определяются в каждом случае, в зависимости от условий закрепления стержня. Всегда имеется возможность записать такие концевые условия, которым соответствуют определенные величины ![]() , найдя которые, можно определить частоты и формы резонансных колебаний. Результирующие перемещения могут быть представлены суммой нормальных форм при поперечных колебаниях стержня в виде:
, найдя которые, можно определить частоты и формы резонансных колебаний. Результирующие перемещения могут быть представлены суммой нормальных форм при поперечных колебаниях стержня в виде:
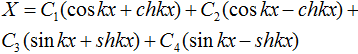
Для свободно опертого стержня постоянные С1 и С2 равняются нулю и С3=С4. Для определения частот колебаний необходимо найти корни частотного уравнения:
![]()
положительные корни данного уравнения:
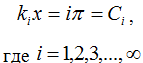
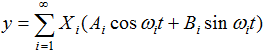 (1)
(1)
Если представить распределение перемещений в виде функции ![]() , а распределение начальных скоростей, придаваемых ударником частицам трубы в виде
, а распределение начальных скоростей, придаваемых ударником частицам трубы в виде ![]() , то результирующее перемещение с использованием выражения (1) в момент времени t:
, то результирующее перемещение с использованием выражения (1) в момент времени t:
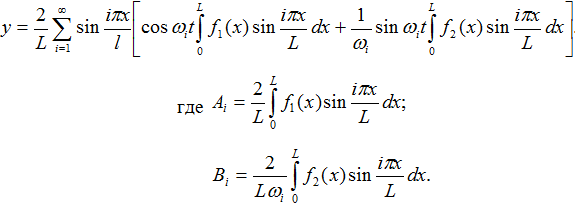
Для описания динамического поперечного перемещения трубопровода длиной L в точке x2 вместо функции воздействия используем начальную скорость движения его частиц v, получаемую трубой в точке при воздействии генератором упругих колебаний с координатой x1, следовательно, ![]() , тогда:
, тогда:
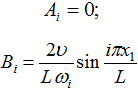
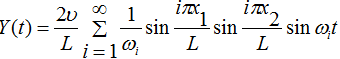 (2)
Для расчета частот колебаний трубы воспользуемся выражением из [6]:
(2)
Для расчета частот колебаний трубы воспользуемся выражением из [6]:
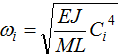 (3)
(3)
где Сi - корни частотного уравнения (10) для моды с номером i; M – погонная масса трубы; L – длина трубы; E – модуль Юнга материала стенки трубы.
В выражении (3) J – момент инерции стенки трубы, выражающийся через диаметр трубы d и толщину ее стенки h [6]:
![]()
Формула (2) описывает сформировавшиеся колебания системы без затухания. Трубопроводная система, функционирующая в реальных условиях, является волноводом с рассеянием, переотражением и поглощением колебаний внешней средой. С учетом данных явлений для получения затухающего импульса следует ввести коэффициенты амплитудно-частотного и амплитудно-временного затухания. Упругие колебания в среде затухают, а фиксируемый полезный сигнал на поверхности трубопровода является зашумленным, следовательно, формулу (2) можно модифицировать следующим образом:
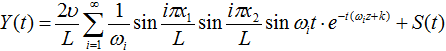 (4)
(4)
где z – амплитудно-частотный коэффициент затухания; k – амплитудно-временной коэффициент затухания; S(t) – помеха.
В формуле (4) присутствует помеха S(t), являющаяся неотъемлемой частью регистрируемых сигналов и формируемая процессом перекачки транспортируемого продукта, внешней окружающей средой и регистрируемым оборудованием. Значения функции S(t) получены посредством записи виброакустического сигнала оборудованием в моменты отсутствия полезного сигнала.
На рис. 1 изображен результат моделирования по формуле (3) для оценки формы моделированного сигнала в сравнении с усредненным импульсом, полученным эмпирически на основе выборки из 30 импульсов на макете трубопровода с параметрами, указанными в таблице 1.
Таблица 1 - Параметры модели
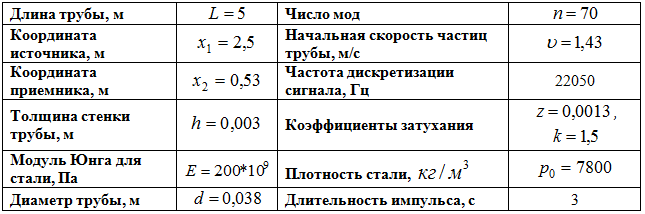
Визуальная оценка параметров по форме импульса и его спектрограмме (рис. 2) позволяет сделать вывод о положительной корреляции значений амплитуд спектра частот вплоть до 1,5 кГц.
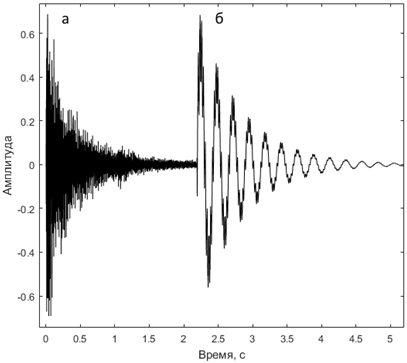
Рис. 1 – Импульсы при ударном воздействии для L = 5м: а) – эмпирический; б) – аналитический
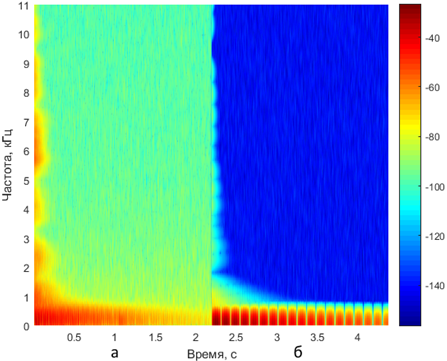
Рисунок 2 – Спектрограмма импульсов при ударном воздействии: а) – эмпирический; б) – аналитический
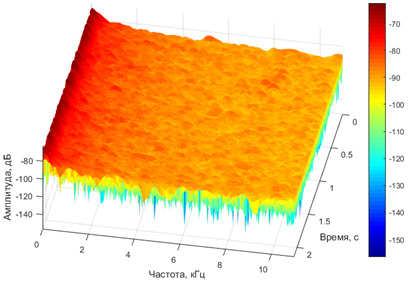
Рис. 3 – Спектрограмма помехи
Произведем оценку спектральной составляющей сигнала модели с использованием ненулевых значений помехи ![]() (рис. 3) посредством суммирования ее значений с функцией полезного сигнала Y(t). На рис. 4 изображен амплитудный спектр сигнала по модели, зашумленного сигнала по модели, среднего эмпирического сигнала и помехи. Наличие помехи S(t) в модели повышает корреляцию аналитического амплитудного спектра с эмпирическим (
(рис. 3) посредством суммирования ее значений с функцией полезного сигнала Y(t). На рис. 4 изображен амплитудный спектр сигнала по модели, зашумленного сигнала по модели, среднего эмпирического сигнала и помехи. Наличие помехи S(t) в модели повышает корреляцию аналитического амплитудного спектра с эмпирическим (![]() ).
).
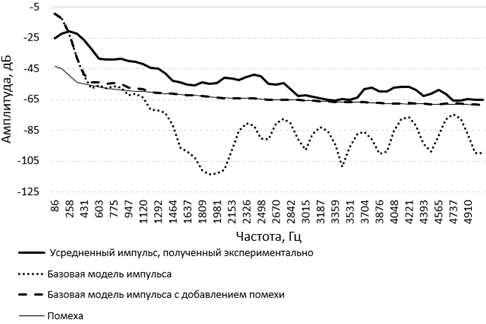
Рис. 4 – Амплитудный спектр сигналов, L = 5м
По результатам моделирования следует сделать вывод о значительной сходимости амплитудного спектра, формируемого моделью, с эмпирическим при воспроизведении частот до 1500 Гц (R2=0,96). С расширением частотного диапазона до 5 кГц коэффициент детерминации амплитудных спектров снижается (R2=0,71).
Проводилось моделирование поперечных колебаний действующего трубопровода протяженностью 200м с диаметром трубы 400мм. Масса перекачиваемой жидкости (вода) была учтена в выражении для частоты:
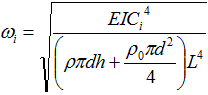
Использование данной модели для аналитического описания вибракустического сигнала в трубопроводе такой протяженности менее эффективно (рис. 5,6), так как корреляция амплитудного спектра с эмпирическим существенно снижается с увеличением дистанции (R2=0,6 для границы 1,5 кГц; R2=0,26 для границы 5 кГц).
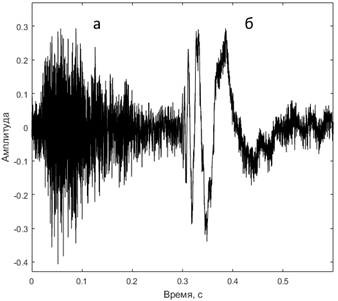
Рис. 5 – Импульсы при ударном воздействии для L = 200м: а) – эмпирический; б) – аналитический
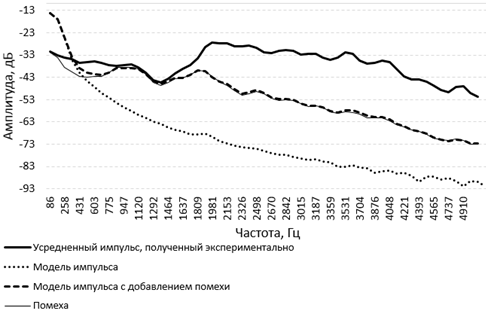
Рис. 6 – Амплитудный спектр сигналов, L = 200м
Таким образом, получена математическая модель виброакустического сигнала, фиксируемого на оболочке трубопровода при ударном воздействии с заданными параметрами. Результаты моделирования позволяют сделать вывод об адекватности представленной модели при проведении расчета колебаний трубопровода для работы в ближней зоне. Значительные отклонения параметров моделированного сигнала от эмпирического на действующем трубопроводе протяженностью 200 м обусловлены отсутствием параметров в модели, учитывающих жесткость основания, которое составляют опоры, распределенные по всей протяженности трубопровода. Модификация выражения для расчета частот собственных колебаний с введением влияния жесткого основания позволит осуществить смещение основных гармоник сигнала в высокочастотную область, что повысит эффективность модели при описании виброакустического сигнала на протяженных трубопроводах.
Список литературы / References
- Федотов А. А. Аналитическое исследование проблемы обнаружения и предотвращения хищений продуктов из магистральных продуктопроводов / А. А. Федотов // Мир нефтепродуктов. Вестник нефтяных компаний. – 2013. – № 9. – С. 43-48.
- Епифанцев, Б. Н. Концепция обеспечения безопасной работы магистральных трубопроводов в условиях внешних воздействий / Б. Н. Епифанцев, А. А. Пятков, А. А. Федотов // Безопасность труда в промышленности. – 2013. – №12. – С. 42–49.
- Способ обнаружения изменений параметров среды в окружении заглубленного магистрального продуктопровода : пат. 2463590 Рос. Федерация : МПК G 01 N 29/04 (2006.01) / Б. Н. Епифанцев, А. А. Федотов ; заявитель и патентообладатель Государственное образовательное учреждение высшего профессионального образования "Сибирская государственная автомобильно-дорожная академия". – № 2011121858/28; заявл. 30.05.2011; опубл. 10.10.2012; Бюл. № 28.
- Тимошенко С. П., Янг Д. Х., Уквер У. Колебания в инженерном деле/Пер. с англ. Л. Г. Корнейчука; Под ред. Э. И. Григолюка. – М.: Машиностроение, 1985. – 472 с.
- Андронов, И.Н. Ресурс надземных трубопроводов. В 2-х ч. Ч. 1. Факторы, ограничивающие ресурс. Стандартные методы испытаний / И.Н. Андронов, А.С. Кузьбожев, Р.В. Агиней. – Ухта: УГТУ, 2008. – 272 с.: ил.
- Миронов М.А., Пятаков П.А., Андреев А.А. Вынужденные изгибные колебания трубы с потоком жидкости // Акустический журнал. – 2010. – Том 56, №5. – С. 684-692.
Список литературы на английском языке / References in English
- Fedotov A. A. Analiticheskoe issledovanie problemy obnaruzhenija i predotvrashhenija hishhenij produktov iz magistral'nyh produktoprovodov [Analytical research of detection and prevention problem of stealing products from main pipelines] / A. A. Fedotov // Mir nefteproduktov [World of oil products]. Vestnik neftjanyh kompanij. – 2013. – № 9. – S. 43-48. [in Russian]
- Epifancev, B. N. Koncepcija obespechenija bezopasnoj raboty magistral'nyh truboprovodov v uslovijah vneshnih vozdejstvij [The concept of ensuring the safe operation of main pipelines in conditions of external influences] / B. N. Epifancev, A. A. Pjatkov, A. A. Fedotov // Bezopasnost' truda v promyshlennosti [Safety of working in industry]. – 2013. – №12. – S. 42–49. [in Russian]
- Sposob obnaruzhenija izmenenij parametrov sredy v okruzhenii zaglublennogo magistral'nogo produktoprovoda [Method for detecting changes in environmental parameters of a buried main pipeline] : pat. 2463590 Ros. Federacija : MPK G 01 N 29/04 (2006.01) / B. N. Epifancev, A. A. Fedotov ; zajavitel' i patentoobladatel' Gosudarstvennoe obrazovatel'noe uchrezhdenie vysshego professional'nogo obrazovanija "Sibirskaja gosudarstvennaja avtomobil'no-dorozhnaja akademija [Siberian State Automobile and Highway University]". – № 2011121858/28; zajavl. 30.05.2011; opubl. 10.10.2012; Bjul. № 28. [in Russian]
- Timoshenko S. P., Jang D. H., Ukver U. Kolebanija v inzhenernom dele [Oscillations in engineering] / Per. s angl. L. G. Kornejchuka; Pod red. Je. I. Grigoljuka. – M.: Mashinostroenie, 1985. – 472 s. [in Russian]
- Andronov, I.N. Resurs nadzemnyh truboprovodov. V 2-h ch. Ch. 1. Faktory, ogranichivajushhie resurs. Standartnye metody ispytanij [Overground pipelines resource. In two parts. Part 1. Factors limiting the resource. Standard test methods] / I.N. Andronov, A.S. Kuz'bozhev, R.V. Aginej. – Uhta: UGTU, 2008. – 272 s.: il. [in Russian]
- Mironov M.A., Pjatakov P.A., Andreev A.A. Vynuzhdennye izgibnye kolebanija truby s potokom zhidkosti [Forced bending vibrations of a tube with a liquid flow] // Akusticheskij zhurnal [Acoustic journal]. – 2010. – Tom 56, №5. – S. 684-692. [in Russian]
