МАШИННОЕ ОБУЧЕНИЕ ПРИ СОЗДАНИИ РАЗВИВАЮЩИХ ЯЗЫКОВЫХ ВИДЕОИГР
Сидоров К.С.1, Ермилов Н.О.2
1ORCID: 0000-0003-0395-286X, студент, 2Старший преподаватель кафедры математики и методики её преподавания,
ФГБОУ ВО «Астраханский государственный университет».
МАШИННОЕ ОБУЧЕНИЕ ПРИ СОЗДАНИИ РАЗВИВАЮЩИХ ЯЗЫКОВЫХ ВИДЕОИГР
Аннотация
В данной статье представлено использование техник машинного обучения и анализа данных для создания адаптивных схем выбора уровней для языковых видеоигр. Описаны предпосылки к созданию подобной системы, а также проведён статистический анализ эффективности построенной схемы на основе данных, собранных с выборки студентов Астраханского государственного университета. Приведено сравнение с более простыми схемами, использованными ранее в процессе разработки, с помощью как классических частотных методов (критерий согласия Пирсона), так и с помощью байесовских методов.
Ключевые слова: машинное обучение, анализ данных, высшее образование, видеоигры, статистика.
Sidorov K.S.1, Ermilov N.O.2
1ORCID: 0000-0003-0395-286X, student, 2 Senior professor of department of mathematics and its teaching methodology, Federal State Budget Educational Institution of Higher Professional Education “Astrakhan State University”
MACHINE LEARNING IN DEVELOPMENT OF VIDEO GAMES FOR LANGUAGE LEARNING
Abstract
This article presents the use of machine learning and data analysis techniques in development of adaptive level selection schemes for video games for language learning. The prerequisites for the development of such a system are described in the paper, as well as a statistical analysis of the effectiveness of the constructed scheme based on data collected from a sample of students of the Astrakhan State University. The comparison is made with the simpler schemes used earlier in the development process, using both classical frequency methods (Pearson consensus test) and Bayesian methods.
Keywords: machine learning, data analysis, higher education, video games, statistics.
ВведениеКак и в любом университете, в Астраханском государственном университете учатся студенты из разных стран, и уровень знания русского языка, разумеется, у них разный. Поскольку для успешного усвоения материала требуется знание русского языка, одна из задач, стоящих перед университетом – подготовить иностранных студентов так, чтобы языковой барьер не мешал им учиться.
С этой целью в АГУ была разработана обучающая видеоигра, основанная на следующей известной идее: игроку выдаётся слово, его задача – за ограниченное время составить как можно больше слов из выданных ему букв. Подобных приложений на рынке, разумеется, представлено много, но они не заточены под обучение языку (в частности, в них отсутствуют продуманные системы уровней).
Как уже было отмечено, уровни сложности игры необходимо градуировать. В то же время простые схемы, неполно учитывающие специфику слова, работали некачественно (понятие качественной модели будет уточнено в разделе «Статистическое сравнение результатов»). Поэтому для построения более эффективной схемы градирования уровней по согласованным с разработчиком техническим заданиям были собраны данные о прохождении игры с разными словами и настройками времени, по которой средствами машинного обучения была построена схема градирования, успешно работающая на практике.
Постановка проблемы
Как уже упоминалось, разрабатываемый продукт основан на составлении как можно большего числа анаграмм заданного слова за ограниченное время. На момент написания статьи интерфейс программы выглядел так, как показано на рис. 1:

Рис. 1 – образец интерфейса приложения
Остаётся неясным, как построить уровни, если зафиксировано время прохождения игры и разыгрываемое слово. Другими словами, нас интересует проблема того, как по заданному слову выбрать пороговые количества слов так, чтобы они могли адекватно задавать степень сложности игры в том смысле, что количество дошедших до того или иного уровня было бы примерно одинаковым.
Насколько нам известно, осознанных попыток решить подобную задачу не предпринималось. В одной из статей на Хабрахабре была попытка учитывать специфику слова для построения системы наград, но она не была подкреплена анализом данных, и некоторые идеи из той статьи будут рассмотрены далее вместе с обоснованием их неэффективности. [1]
Описание выборки
Для дальнейшего анализа была собрана выборка данных о прохождении игры. Более подробно, она содержит 989 записей, каждая из которых содержит:
разыгрываемое слово;
максимальное возможное количество слов, которое можно в нём найти;
время прохождения;
количество найденных слов.
Пять первых записей выборки приведены в таблице 1.
Таблица 1 – Образец формата записей в выборке
| Слово | Максимальное количество | Время на игру, минуты | Результат |
| математика | 129 | 7 | 13 |
| алгебра | 97 | 7 | 6 |
| геометрия | 229 | 7 | 15 |
| логика | 76 | 5 | 16 |
| графика | 77 | 5 | 24 |
Как можно видеть уже по первым записям, выборка достаточно вариативна – например, разыгрывались слова разной длины и с разным потенциалом на поиск слов.
В то же время можно заметить, что большинство игроков не угадывают очень много возможных слов (см. рис. 2). С одной стороны, это объясняется ограниченностью времени, а с другой – наличием редких слов, неизвестных даже многим носителям языка
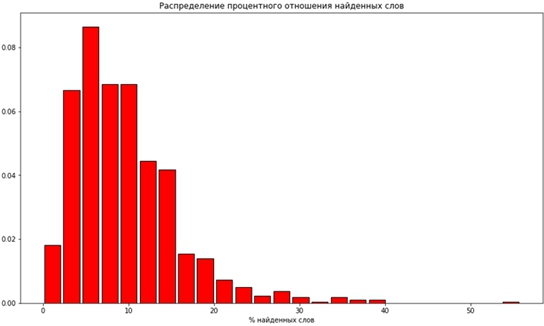
Рис. 2 – гистограмма распределения процентного отношения найденных слов
Как видим, основная масса не находит больше 15% слов, а больше 50% было найдено только в 1 игре (напомним, что в выборке их 989).
Математическая модель
Для дальнейшего анализа нам понадобится математическая модель зависимости количества найденных слов от времени. Для этого мы будем использовать модель, известную из ядерной физики как простейшую модель числа нераспавшихся частиц [2]. А именно, будем считать, что если всего в слове можно найти ![]() слов, то в момент времени t игрок найдёт
слов, то в момент времени t игрок найдёт ![]() слов. На качественном уровне это можно понимать так: сначала игрок находит слова с постоянной скоростью λ, после чего приходит «насыщение», и он начинает находить слова всё медленнее и медленнее, но асимптотически при
слов. На качественном уровне это можно понимать так: сначала игрок находит слова с постоянной скоростью λ, после чего приходит «насыщение», и он начинает находить слова всё медленнее и медленнее, но асимптотически при ![]() игрок находит все слова.
игрок находит все слова.
Параметр λ в данной модели отражает, как уже упоминалось, скорость «прорешивания» слова. Заметим, что для более опытных игроков этот параметр будет больше – это будет существенно для построения системы уровней на основе данной модели.
Эту модель пока что нельзя использовать напрямую, потому что есть скрытый параметр λ, поэтому дальнейшее изложение будет разворачиваться вокруг оценки этого параметра. Поскольку в нашей выборке хранятся только параметры ![]() то мы можем построить эмпирическую оценку на скрытый параметр следующим образом:
то мы можем построить эмпирическую оценку на скрытый параметр следующим образом: ![]() .
.
Настройка параметров с помощью машинного обучения
Как уже отмечалось, мы ищем зависимость λ от параметров слова. Предлагается искать эту зависимость в классе параметрических зависимостей вида ![]() , где x – вектор параметров слова (содержащий, в частности, максимальное доступное количество слов), а, w, b – пока что неизвестные параметры, задающие зависимость.
, где x – вектор параметров слова (содержащий, в частности, максимальное доступное количество слов), а, w, b – пока что неизвестные параметры, задающие зависимость.
Именно такой вид зависимости обосновывается графиком, представленном на рис. 3.
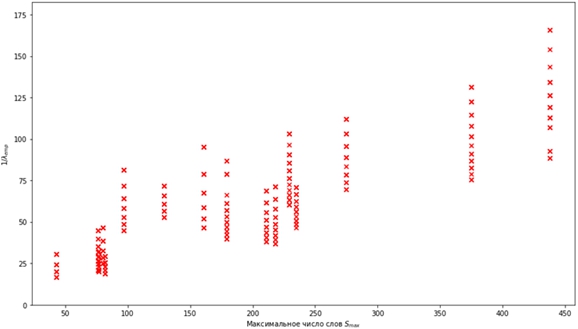
Рис. 3 – диаграмма рассеяния для зависимости ![]() от максимального числа слов
от максимального числа слов
Как можно видеть на приведённой диаграмме, зависимость ![]() можно хотя бы с точностью до случайного шума считать линейной. Из этого возникает следующая задача машинного обучения: по выборке, состоящей из параметров слова и оценки
можно хотя бы с точностью до случайного шума считать линейной. Из этого возникает следующая задача машинного обучения: по выборке, состоящей из параметров слова и оценки ![]() , построить линейную модель для предсказания ξ по остальным переменным. Для ясности, в таблице 2 приводим примерный вид выборки в том формате, в котором она используется при применении алгоритмов машинного обучения (использованы те же объекты в том же порядке, что и в таблице 1).
, построить линейную модель для предсказания ξ по остальным переменным. Для ясности, в таблице 2 приводим примерный вид выборки в том формате, в котором она используется при применении алгоритмов машинного обучения (использованы те же объекты в том же порядке, что и в таблице 1).
Таблица 2 – Образец формата записей в выборке, составленной для поиска модели для ξ (для простоты указана лишь одна свободная переменная)
| Максимальное количество | ξ, эмпирическая оценка |
| 129 | 0,015 |
| 97 | 0,009 |
| 229 | 0,009 |
| 76 | 0,047 |
| 77 | 0,075 |
В такой постановке получается стандартная задача линейной регрессии, для решения которой существует множество инструментов [3]. Перед применением алгоритма, впрочем, оказалось нужным для каждого слова удалить все объекты, не находящиеся между 25-ой и 75-ой процентилью по количеству найденных слов. Таким образом, из выборки были удалены нетипично слабые и нетипично сильные игроки – из-за очень большой разнородность уровня знаний игроков в области лексики русского языка данные получились очень зашумлёнными, без подобной процедуры очистки построить полезные выводы не представлялось возможным. В результате подобной очистки в выборке осталось лишь 563 объекта.
К оставшимся объектам была применена стандартная модель линейной регрессии с L1-регуляризатором [4]. На кросс-валидации с 3 проходами модель показала среднее значение коэффициента детерминации 0,539. Это можно интерпретировать следующим образом: модель смогла «объяснить» 53,9% дисперсии в данных (для сравнения, константная модель по определению данного коэффициента объясняет 0% дисперсии) [5]. С учётом того, что данные остались достаточно зашумлёнными даже после удаления части данных (рис. 3 был построен именно на сокращённой выборке), это можно расценивать как положительный результат, который можно использовать далее для других задач (например, для оценки порогов уровней).
В конечном итоге была найдена следующая зависимость: ![]() . В данной зависимости фигурирует только одна свободная переменная –
. В данной зависимости фигурирует только одна свободная переменная – ![]() , чему есть строгое обоснование. Поскольку L1-регуляризатор обладает свойством удаления признаков, не объясняющих вариативность данных [4], то во время исследования в модель добавлялись признаки, которые могут косвенным образом объяснять сложность слова – например, его длина, количество гласных, отношение количества гласных к длине слова. Все подобные признаки моделью отклонялись как несущественные (если точнее, модель выставляла им нулевые коэффициенты), что говорит о том, что такие признаки не имеют значения для игроков при условии, что известно максимально количество слов. В частности, это опровергает схемы из упомянутых статей на Хабрахабре и позволяет перейти к решению основной поставленной задачи.
, чему есть строгое обоснование. Поскольку L1-регуляризатор обладает свойством удаления признаков, не объясняющих вариативность данных [4], то во время исследования в модель добавлялись признаки, которые могут косвенным образом объяснять сложность слова – например, его длина, количество гласных, отношение количества гласных к длине слова. Все подобные признаки моделью отклонялись как несущественные (если точнее, модель выставляла им нулевые коэффициенты), что говорит о том, что такие признаки не имеют значения для игроков при условии, что известно максимально количество слов. В частности, это опровергает схемы из упомянутых статей на Хабрахабре и позволяет перейти к решению основной поставленной задачи.
Реализация уровней сложности
Как уже упоминалось, большие значения параметра скорости при прочих равных в нашей модели задают более высокий уровень мастерства игрока. Поэтому возможна следующая реализация уровней: пусть зафиксировано слово и время t. По параметрам слова (как было показано выше) оцениваем ![]() . Сделав это, вычисляем величину S(t), используя
. Сделав это, вычисляем величину S(t), используя ![]() – это будет средний уровень сложности. Лёгкий (трудный) уровень теперь получаются подстановкой меньшего (большего) значения λ в выражение для S(t).
– это будет средний уровень сложности. Лёгкий (трудный) уровень теперь получаются подстановкой меньшего (большего) значения λ в выражение для S(t).
Отметим, что эмпирически величина ![]() распределена нормально, что отражено на Q-Q графике [6] на рис. 4, построенном с помощью оценок
распределена нормально, что отражено на Q-Q графике [6] на рис. 4, построенном с помощью оценок ![]() для всех объектов выборки.
для всех объектов выборки.
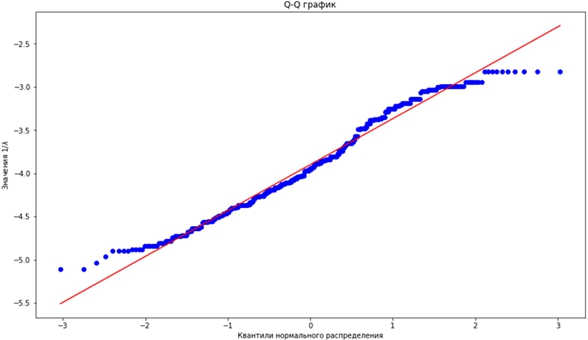
Рис. 4 – Q-Q график для квантилей нормального распределения и значений исследуемой величины
Из графика видно, что соответствующие квантили двух распределений – нормального и эмпирического – очень похожи (особенно в зоне типичных значений), что означает, что ![]() хотя бы приближённо можно считать нормально распределённой.
хотя бы приближённо можно считать нормально распределённой.
Соответственно, если считать, что ![]() , то тогда при выборе подходящего α значения
, то тогда при выборе подходящего α значения ![]() окажутся (соответственно) первым, вторым и третьим квартилем распределения, то есть поделят игроков на четыре примерно равные группы в зависимости от степени опыта – как раз то, что и должна делать хорошая схема построения уровней.
окажутся (соответственно) первым, вторым и третьим квартилем распределения, то есть поделят игроков на четыре примерно равные группы в зависимости от степени опыта – как раз то, что и должна делать хорошая схема построения уровней.
Переходя от логарифмов к исходным величинам, получаем формулы для построения лёгкого, среднего и трудного уровней получаются выбором λ соответственно ![]() , и для некоторого K (в наших экспериментах неплохие результаты давало K=0.7).
, и для некоторого K (в наших экспериментах неплохие результаты давало K=0.7).
Статистическое сравнение результатов
Ранее в приложении использовалась следующая схема уровней (далее будем называть её жёсткой – в противовес мягкой, адаптивной схеме, разработанной выше): для прохождения лёгкого уровня требовалось найти 0.04![]() , среднего – 0.08
, среднего – 0.08![]() , трудного – 0.12
, трудного – 0.12![]() .
.
Поскольку нашим основным требованием к уровням сложности является равное разделение игроков по группам, то был проведён следующий тест: для каждого слова были выписаны уровни в соответствии с обеими схемами, после чего для каждого слова было рассчитано количество игроков, дошедших до того или иного уровня (всего для каждого слова получилось 4 числа).
Пример выборки, построенной для статистического анализа – в таблице 3.
Таблица 3 – Количество дошедших до того или иного уровня (по жёсткой схеме) для первых 5 слов выборки
| Слово | Не дошло до 1 уровня | Дошло до 1, но не до 2 уровня | Дошло до 2, но не до 3 уровня | Дошло до 3 уровня |
| математика | 1 | 4 | 31 | 27 |
| алгебра | 1 | 8 | 24 | 30 |
| геометрия | 2 | 20 | 27 | 14 |
| логика | 0 | 4 | 12 | 40 |
| графика | 0 | 3 | 6 | 47 |
Поскольку перед нами стоит требование равномерности, разумно применить ко всем словам критерий согласия Пирсона [7]. (Требуемый уровень значимости везде – 5%). В результате применения критерия к жёсткой схеме только для одного слова – «розетка» – нельзя отклонить нулевую гипотезу (которая в критерии согласия Пирсона формулируется как равномерность исследуемого распределения). В мягкой схеме нулевая гипотеза не отклоняется уже для шести слов – «геометрия», «розетка», «монетизация», «линолеум», «клавиатура», «праздничный». Учитывая, что выборка содержит очень большое количество шума, это уже позволяет сделать вывод о том, что мягкая схема представляет собой качественное улучшение по сравнению с жёсткой.
Также был проведён ещё один тест, в котором напрямую оценивалась энтропия полученных распределений игроков – из наших рассуждений следует, что чем выше энтропия разбиения, тем лучше работает схема построения уровней.
Для этого использовалась следующая вероятностная модель:
![]()
Здесь:
![]() – гиперпараметр, отвечающий за априорное знание о количестве объектов (мы использовали
– гиперпараметр, отвечающий за априорное знание о количестве объектов (мы использовали ![]() );
);
p – вероятностное распределение, задающую вероятность увидеть игрока, дошедшего до соответствующего уровня;
x – конкретное «наблюдение», то есть уровень, до которого дошёл игрок.
Пусть мы увидели ![]() игроков, дошедших до того или иного уровня. (Это ровно те числа, которые приведены в таблице 3). Тогда, как известно, по правилу Байеса можно получить апостериорное распределение на p, которое будет равно
игроков, дошедших до того или иного уровня. (Это ровно те числа, которые приведены в таблице 3). Тогда, как известно, по правилу Байеса можно получить апостериорное распределение на p, которое будет равно ![]() – вновь распределение Дирихле, но с другими параметрами [8].
– вновь распределение Дирихле, но с другими параметрами [8].
Далее мы провели следующий эксперимент: для каждой из схем построили указанное байесовское апостериорное распределение, после чего построили случайную выборку для величины H(p) – энтропии Шеннона [9] – и эмпирически оценили 95%-ный доверительный интервал для неё. (Поскольку апостериорное распределение мы получили в явном виде, то для эмпирической оценки мы могли использовать достаточно много значений p – в наших экспериментах результаты перестали меняться после того, как размер выборки превысил 10 миллионов).
В результате для шести слов - «логика», «графика», «монетизация», «линолеум», «клавиатура», «праздничный» - доверительный интервал для энтропии мягкой схемы лежал целиком правее, чем доверительный интервал для жёсткой схемы, что можно интерпретировать следующим образом: мягкая схема на этих словах устойчиво даёт статистически значимо более равномерное распределение. Обратной ситуации не возникало ни разу; более того, точечные оценки на энтропию мягкой схемы были больше для 14 слов из 16. Полные результаты запуска – в таблице 4.
Таблица 4 – Эмпирические доверительные интервалы для двух схем
| Слово | Доверительный интервал жёсткой схемы | Доверительный интервал мягкой схемы | Статистически эффективная схема |
| математика | [0.85, 1.15] | [0.94, 1.26] | - |
| алгебра | [0.94, 1.21] | [0.94, 1.19] | - |
| геометрия | [1.07, 1.29] | [1.24, 1.28] | - |
| логика | [0.65, 1.03] | [1.18, 1.37] | Мягкая схема |
| графика | [0.43, 0.88] | [1.04, 1.31] | Мягкая схема |
| розетка | [1.21, 1.37] | [1.24, 1.38] | - |
| монетизация | [0.77, 1.09] | [1.22, 1.38] | Мягкая схема |
| потолок | [0.75, 1.07] | [0.75, 1.07] | - |
| аудитория | [1.04, 1.27] | [1.10, 1.33] | - |
| краска | [0.61, 0.97] | [0.93, 1.23] | - |
| линолеум | [0.95, 1.25] | [1.28, 1.38] | Мягкая схема |
| куртка | [1.12, 1.31] | [1.16, 1.35] | - |
| компьютер | [0.96, 1.25] | [0.97, 1.27] | - |
| сковорода | [1.04, 1.31] | [1.00, 1.29] | - |
| клавиатура | [0.74, 1.08] | [1.25, 1.38] | Мягкая схема |
| праздничный | [0.82, 1.18] | [1.20, 1.37] | Мягкая схема |
Отметим, что ещё одним достоинством представленной схемы (как видно по таблице 4) является её устойчивость – даже когда мягкая схема в чём-то проигрывала жёсткой, её всё равно удавалось производить достаточно сбалансированные разбиения.
Заключение
В данной статье была рассмотрена, построена и проанализирована система уровней, способная адаптироваться под параметры конкретного слова и (после модификации алгоритма с учётом возникающей специфики задачи online learning [10]) к специфике игроков.
Всё исследование было подкреплено конкретными данными и статистическими оценками, построенными на них, что подтверждает работоспособность данной модели в рассматриваемой задаче.
В качестве дальнейших улучшений рассматривается расширение данной схемы на выбор не только интересных уровней сложности, но и интересных временных интервалов (построение быстрых или длинных игр в зависимости от слова). Также рассматривается построение системы наград на основе данных, что может также быть очень полезно при геймификации приложения и, как следствие, вовлечении пользователей в процесс изучения лексики.
Список литературы / References
- Создание игры «Слова из Слова» [Электронный ресурс] // Habrahabr. – 2016. – URL: https://habrahabr.ru/post/308256/ (дата обращения: 16.11.2017).
- Rutherford E. A comparative study of the radioactivity of radium and thorium. / Ernest Rutherford, Frederick Soddy // Philosophical Magazine – 1903. – Vol. 5 – P. 445-457 – doi:10.1080/14786440309462943
- Pedregosa F. Scikit-learn: Machine Learning in Python. / Fabian Pedregosa, Gaël Varoquaux, Alexandre Gramfort and others // Journal of Machine Learning Research – 2011. – Vol. 12 – P. 2825-2830.
- Tibshirani R. Regression Shrinkage and Selection via the Lasso. / Robert Tibshirani // Journal of the Royal Statistical Society. Series B (Methodological) – 1996. – Vol. 58 – P. 267-288.
- Glantz S. Primer of Applied Regression and Analysis of Variance. / Stanton A. Glantz, Bryan K. Slinker. - McGraw-Hill, 1990 – 949 p.
- NIST/SEMATECH e-Handbook of Statistical Methods, 1.3.3.24. Quantile-Quantile Plot [Электронный ресурс] // National Institute of Standards and Technology. – 2012. – URL: http://www.itl.nist.gov/div898/handbook/eda/section3/qqplot.htm (дата обращения: 16.11.2017).
- Pearson K. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. / Karl Pearson // The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science – 1900. – Vol. 50 – P. 157-175 – doi:10.1080/14786440009463897
- Agresti A. Bayesian inference for categorical data analysis. / Alan Agresti, David B. Hitchcock // Statistical Methods and Applications – 2005. – Vol. 14 – P. 297-330 – doi:10.1007/s10260-005-0121-y
- Shannon C. E. A Mathematical Theory of Communication. / Claude E. Shannon // Bell System Technical Journal – 1948. – Vol. 27 – P. 379-423 – doi:10.1002/j.1538-7305.1948.tb01338.x
- Bottou L. Online Learning and Stochastic Approximations. / Léon Bottou – 1998.
Список литературы на английском языке / References in English
- Sozdanie igry «Slova iz Slova» [Creation of the game “Words from Words”] [Electronic resource] // Habrahabr. – 2016. – URL: https://habrahabr.ru/post/308256/ (accessed: 16.11.2017). [in Russian]
- Rutherford E. A comparative study of the radioactivity of radium and thorium. / Ernest Rutherford, Frederick Soddy // Philosophical Magazine – 1903. – Vol. 5 – P. 445-457 – doi:10.1080/14786440309462943
- Pedregosa F. Scikit-learn: Machine Learning in Python. / Fabian Pedregosa, Gaël Varoquaux, Alexandre Gramfort and others // Journal of Machine Learning Research – 2011. – Vol. 12 – P. 2825-2830.
- Tibshirani R. Regression Shrinkage and Selection via the Lasso. / Robert Tibshirani // Journal of the Royal Statistical Society. Series B (Methodological) – 1996. – Vol. 58 – P. 267-288.
- Glantz S. Primer of Applied Regression and Analysis of Variance. / Stanton A. Glantz, Bryan K. Slinker. - McGraw-Hill, 1990 – 949 p.
- NIST/SEMATECH e-Handbook of Statistical Methods, 1.3.3.24. Quantile-Quantile Plot [Electronic resource] // National Institute of Standards and Technology. – 2012. – URL: http://www.itl.nist.gov/div898/handbook/eda/section3/qqplot.htm (accessed: 16.11.2017).
- Pearson K. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. / Karl Pearson // The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science – 1900. – Vol. 50 – P. 157-175 – doi:10.1080/14786440009463897
- Agresti A. Bayesian inference for categorical data analysis. / Alan Agresti, David B. Hitchcock // Statistical Methods and Applications – 2005. – Vol. 14 – P. 297-330 – doi:10.1007/s10260-005-0121-y
- Shannon C. E. A Mathematical Theory of Communication. / Claude E. Shannon // Bell System Technical Journal – 1948. – Vol. 27 – P. 379-423 – doi:10.1002/j.1538-7305.1948.tb01338.x
- Bottou L. Online Learning and Stochastic Approximations. / Léon Bottou – 1998.
