ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ МНОГОСЛОЙНЫХ КРУГЛЫХ ПЛАСТИН ПЕРЕМЕННОЙ ТОЛЩИНЫ ИЗ НЕЛИНЕЙНО-УПРУГОГО МАТЕРИАЛА
ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ МНОГОСЛОЙНЫХ КРУГЛЫХ ПЛАСТИН ПЕРЕМЕННОЙ ТОЛЩИНЫ ИЗ НЕЛИНЕЙНО-УПРУГОГО МАТЕРИАЛА
Научная статья
Садигов И.Р. *
Азербайджанский Архитектурно-Строительный Университет, Баку, Азербайджан
* Корреспондирующий автор (ismayilsadigov50[at]gmail.com)
АннотацияТочные методы решения задачи изгиба могут применяться лишь для некоторых частных случаев, когда пластина простой конфигурации и постоянной толщины. Эта задача также ограничена граничными условиями, и может быть решена лишь при определенных их видах. В настоящем исследовании рассмотрены вопросы устойчивости круглых многослойных пластин переменной толщины с функциональной градуировкой, подвергаемых радиальному сжатию, на основе теории пластин сдвиговых деформаций первого порядка и поля нелинейных смещений фон Кармана.
Ключевые слова: устойчивость, деформация, изгиб, круглая, кольцевая, пластина, переменная толщина.
STUDY OF STABILITY OF MULTILAYER ROUND PLATES OF VARIABLE THICKNESS FROM NONLINEAR ELASTIC MATERIAL
Research article
Sadigov I.R. *
Azerbaijan University of Architecture and Construction, Baku, Azerbaijan
* Corresponding author (ismayilsadigov50[at]gmail.com)
AbstractPrecise methods for solving the problem of bending can be used only for special cases where the plate is of simple configuration and constant thickness. This task is also limited by boundary conditions, and can be solved only under certain types. This study examines the stability of round multi-layered plates of variable thickness with functional grading subjected to radial compression based on the theory of plates of first-order shear deformations and the field of non-linear von Karman displacements.
Keywords: stability, deformation, bending, round, ring, plate, variable thickness.
ВведениеСтремительное развитие нелинейной теории круглых кольцевых пластинок переменной толщины из нелинейно-упругого материала обусловлено практическими и научными потребностями применения.
Актуальность темы исследований и дальнейшее совершенствование методов расчета устойчивости круглых и кольцевых пластин обусловлено широким распространением и применением круглых кольцевых пластин с использованием новых материалов, и изменением их толщин в необычных условиях при больших интенсивностях внешних воздействий.
Основная часть
Многие современные конструкционные решения состоят из элементов, которые можно классифицировать как пластинки. Данные пластинки могут быть постоянной или переменной толщины, различной сложной геометрической формы с вырезами или без них, а также на них могут оказывать влияния не только силовые, но и температурные воздействия.
Прогнозирование устойчивости силовых тонкостенных элементов конструкций (пластин) переменной толщины круглой кольцевой формы из нелинейно-упругого материала является важным моментом в проектировании всей конструкции в целом.
Развитие нелинейной динамики пластин, в том числе круглых кольцевых, и также оболочек, берёт своё начало, со второй половины ХХ в.
Особенно важное значение приобретает применение пластин переменной толщины для облегчения конструкций, при использовании в высокоскоростных самолетах. С особой аккуратностью распределения толщины можно добиться увеличения деформации пластины по сравнению с аналогом по толщине [1].
С целью создания пластин переменной толщины значительный интерес представляет применение функциональных композитных материалов, свойства которых могут различаться с различных сторон, сохраняя однородность материала. Эти материалы, зачастую, построены из смеси керамики и металла, и они могут сохранять свои функциональные характеристики в условиях температурных перепадов, таких как наблюдаются в ядерных реакторах и на высокоскоростных самолетах. Низкая теплопроводность керамики обеспечивает жаропрочность. Но с другой стороны, пластичный метал предотвращает разрушения, вызванные тепловыми напряжениями.
Значительное число исследований были сделаны на предмет потери устойчивости пластин постоянной толщины из функциональных композитных материалов. Тем не менее, в настоящее время предмет исследования пластин переменной толщины из данного типа материалов изучен в недостаточной степени. Пластины из подобного типа материалов будут составлять значительную часть структурного применения в будущем в аэрокосмической и в иных отраслях, где снижение веса конструктивных элементов имеет важное значение [2].
В данном исследовании предлагается исследование термостабильности и устойчивости круглых кольцевых пластин переменной толщины из нелинейно-упругого функционально–композитного материала.
Рассмотрим круглую пластину с радиусом b, которая находится симметрично посередине плоскости.
Пластина находится под равномерным напряжение с шагом увеличения или уменьшения ΔS.
Начало цилиндрической системы координат лежит в центре плоскости. Здесь r и z определяют радиальное направление и толщину соответственно, ψ определяет вращение вокруг радиальной оси, u и w – смещения в направлениях r и z соответственно.
Условное изображение геометрии круглой пластины переменной толщины представлено на рис. 1.
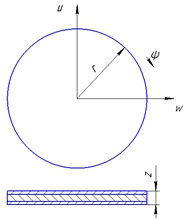
Рис. 1 – Геометрия круглой пластины переменной толщины (изображение условное)
Круглая пластина, представленная в данном исследовании для изучения, может рассматриваться как сэндвич-пластина с однородным ядром переменной толщины, hH(r), и двумя лицевыми панелями из функционального композитного материала с постоянной толщиной, hf. Поэтому общая толщина пластины, h(r), будет функцией от r.

где:
![]() – толщины среднего слоя по центру и краю пластины соответственно;
– толщины среднего слоя по центру и краю пластины соответственно;
р – определяет профиль толщины.
Хотя формулировка и метод являются общими для круглой пластины с любым профилем по толщине, анализ проводится только на пластинах с линейным и параболическим профилями.
Пластина состоит из трех слоев так, что k-ый слой находится между координатами zk и zk+1.

Учитывая, что пластина с постоянным объемом среднего слоя, VH, то соотношение между геометрическими параметрами дают:
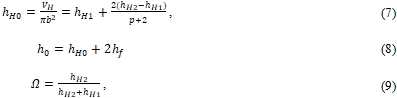
где:
![]() – толщина среднего слоя (равномерная толщина);
– толщина среднего слоя (равномерная толщина);
![]() – параметр конусности в диапазоне от 0 до 1, определяя объемное распределение среднего слоя в радиальном направлении.
– параметр конусности в диапазоне от 0 до 1, определяя объемное распределение среднего слоя в радиальном направлении.
Свойства материала лицевых слоев пластины из функционального композитного материала определяются модулем Юнга и являются функциями объемных долей керамики и металла Vc и Vm, тогда:

где:
N – индекс объемной доли в диапазоне от 0 до ∞.
Чтобы учесть нелинейность материала и потерю устойчивости, отношения осесимметричного смещения деформации запишем на основе теории пластин Кармана:



где:
(),r – указатель дифференцирования по r.
Отношения между напряжением и деформацией основаны на законе Гука, а коэффициент Пуассона ν считается постоянной величиной:
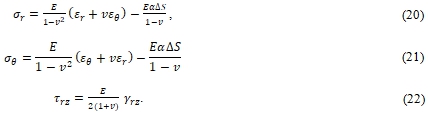
Полученные в результате силы и моменты напряжений определяются следующим образом:

где:
K – поправочный коэффициент сдвига в теории пластин деформации сдвига первого порядка, который соответствует 5/6.
Подставляя уравнения (20) – (22) в уравнения (23) – (25) получим следующие соотношения между результирующими силами, моментами и напряжениями:
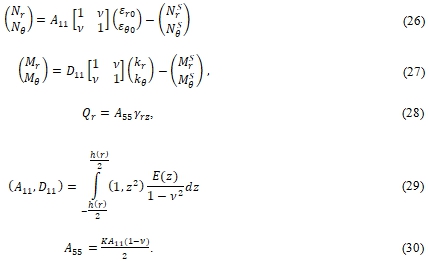

Уравнения равновесия круглой пластины с осесимметричными деформациями могут быть получены с использованием метода стационарной потенциальной энергии следующим образом:
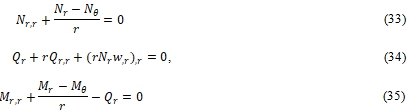
Подставляя уравнения (13) – (19) и (26) – (28) в уравнение (33) – (35) получим уравнения равновесия в терминах смещения компоненты:
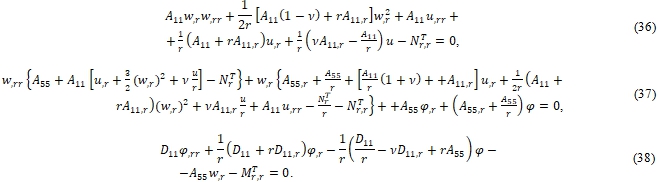
Из полученного выше уравнения можно получить все конфигурации пластины. Возможны два типа равновесных конфигураций пластины: под нагрузкой в плоскости, которая отклонена и изогнутыми конфигурациями при закреплении.
Когда происходит потеря устойчивости конфигурация пластины превратится из отклоненной конфигурации в изогнутую.
Пересечение этих двух равновесных конфигураций называется точкой бифуркации. Эту точку можно получить путем решения линейных дифференциальных уравнений устойчивости [3].
Уравнения устойчивости можно выразить следующим образом:
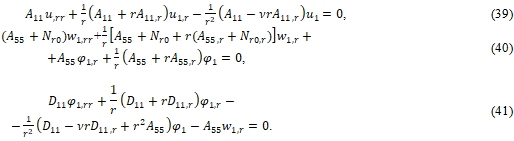
Уравнения устойчивости являются однородными и линейными и имеют решения только для дискретных значений приложенной нагрузки, что относится к проблеме собственных значений.
Наименьшее собственное значение называется критической нагрузкой потери устойчивости Pcr.
Следует отметить, что уравнение (39) отделено от формул (40) и (41).
Граничные условия для уравнений устойчивости принимаются следующие:
Центральный слой:
![]()
Заключение
Предложена методика определения устойчивости круглых многослойных пластин переменной толщины из функциональных композитных материалов при радиальном сжатии на основе теории пластин сдвиговых деформаций первого порядка и поля нелинейных смещений фон Кармана.
Предложенный метод актуален для определения устойчивости как круглых, так и кольцевых пластин переменной толщины из нелинейно-упругого материала, в том числе при радиальном сжатии.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Моховнев Д.В. Устойчивость ортотропных пластин при термосиловом нагружении: диссертация кандидата физико-математических наук: 01.02.04 / Моховнев Д.В. – Новосибирск, 2006. – 236 с.: ил.
- Морс Ф.М. Методы теоретической физики / Морс Ф.М., Фешбах Г. // Том 2. – М.: Издательство иностранной литературы, 1960. – 898 с. Пер. с англ. Под ред. С.П. Аллилуева и др.
- Ozakca M. Buckling analysis and shape optimization of elastic variable thickness circular and annular plates / M. Ozakca, N. Taysi, F. Kolcu – I. Finite element formulation. Eng Struct 2003; pp.181-92.
Список литературы на английском языке / References in English
- Mokhovnev D.V. Ustoichivost ortotropnykh plastin pri termosilovom nagruzhenii: dissertatsiya kandidata fiziko-matematicheskikh nauk: 01.02.04 [Stability of Orthotropic Plates at Thermosoil Loading: Thesis of PhD in Physics and Mathematics: 01.02.04] / Mokhovnev D.V. – Novosibirsk, 2006. – 236 pp., Ill. [In Russian]
- Mors F.M. Metody teoreticheskoi fiziki. Tom 2 [Methods of Theoretical Physics. Volume 2] / Mors F.M., Feshbach G. – M.: Publishing House of Foreign Literature, 1960. – 898 p. Tranls. from English. Ed. by S.P. Alliluyeva et al. [In Russian]
- Ozakca M. Buckling analysis and shape optimization of elastic variable thickness circular and annular plates / M. Ozakca, N. Taysi, F. Kolcu – I. Finite element formulation. Eng Struct 2003; pp.181-92.
