ИСПОЛЬЗОВАНИЕ ПОИСКА ПУТИ В АВТОМАТИЗАЦИИ
Фахрутдинов А.Р.
Студент,
Томский Политехнический Университет
ИСПОЛЬЗОВАНИЕ ПОИСКА ПУТИ В АВТОМАТИЗАЦИИ
Аннотация
Цель исследования – выявить самый приемлемый для задач автоматизации алгоритм нахождения пути, разобрать его плюсы и минусы, а также рассмотреть способы его реализации.
Ключевые слова: нахождение пути, автоматизация, кратчайший путь, алгоритм А*.
Fakhrutdinov A.R.
Student,
Tomsk Polytechnic University
USING OF PATHFINDING IN AUTOMATION
Abstract
Objective of this research – find the most suitable for automation’s tasks pathfinding algorithm, determine pros and cons, find out way of implementation.
Key words: pathfinding, automation, shortcut, A* algorithm.
Каждый день человек, пытается найти более легкое решение, наиболее прочный механизм и кратчайший путь. Почти каждый день мы сталкиваемся вопросом, как его определить и куда двигаться, чтобы не потерять много времени.
В автоматизации, робототехники и во многих других сферах, встает вопрос о необходимости нахождения кратчайшего и более удобного пути.
Самое большое распространение получили в компьютерных играх, где принцип нахождения пути для юнитов очень необходим. Именно поэтому в настоящее время применяются самые различные и изощрённые методы для его нахождения.
Цель данной работы является определение метода нахождения пути для глобальных карт. Актуальность данной темы вытекает из того факта, что реализация данной задачи необходима в различных сферах жизни человека.
По своей сути любой алгоритм поиска пути основывается на теории графов. Граф - это совокупность непустого множества вершин и множества пар вершин (связей между вершинами).[1,2]
Объекты представляются как вершины, или узлы графа, а связи – как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах., Начиная с одной (стартовой) точки и исследуя смежные узлы до тех пор, пока не будет достигнут узел назначения (конечный узел). Кроме того, в алгоритмы поиска пути в большинстве случаев заложена также цель найти самый короткий путь. Некоторые методы поиска на графе, такие как поиск в ширину, могут найти путь, если дано достаточно времени. Другие методы, которые «исследуют» граф, могут достичь точки назначения намного быстрее. Здесь можно привести аналогию с человеком, идущим через комнату. Человек может перед началом пути заранее исследовать все характеристики и препятствия в пространстве, вычислить оптимальный маршрут и только тогда начать непосредственное движение. В другом случае человек может сразу пойти в приблизительном или предполагаемом направлении цели и потом, уже во время пути, делать корректировки своего движения для избегания столкновений с препятствиями.
К самым известным и популярным алгоритмам поиска пути относятся такие алгоритмы:
- Алгоритм поиска A*
- Алгоритм Дейкстры
- Волновой алгоритм
- Навигационная сетка (Navmesh)
- Иерархические алгоритмы
- Обход препятствий
- Алгоритм «Разделяй и властвуй»
- Алгоритм поворота Креша
В данной работе мы рассмотрим комбинированная алгоритм, объединяющий в себе иерархический и волновой алгоритмы.
Данный алгоритм позволяет определять путь на огромных картах, что необходимо как для компьютерных игр, так и для автоматизации, например в движении автомобиля или самолета по дорогам и авиационным линиям.
Иерархический подход довольно сильно напоминает то, как путь строит сам человек. В случае если надо добраться в другой город, сначала строится путь по городам (верхняя иерархия), а потом уже прокладывается детальный путь учитывая улицы городов, через которые предстоит пройти (нижняя иерархия). Примерно таким же способом работает алгоритм HPA*:
– Разбиваем карту на зоны
– Строим граф из глобальных зон учитывая проходы между ними
– Ищем путь сначала по зонам, а дальше в каждой отдельной зоне
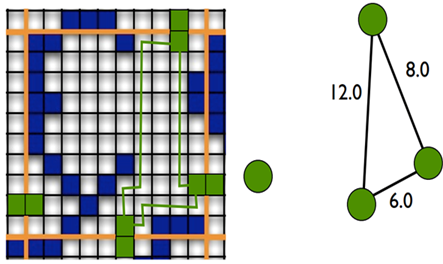
Определения пути в отдельной зоне рассмотрим рисунок 1. Определение пути происходит по алгоритму подобному алгоритму A*.Далее применяя метод рекурсии (процесс повторения элементов самоподобным образом) применяем его для остальных областей.
Рис. 1
На рис. 2 представлена примерная карта местности, на которой уже определены все наикротчайшие пути между зонами.
Далее остается лишь получить координаты начала и конца и найти кратчайшие пути от этих точек до точек выхода из зоны, и определить длину остальной части пути.
К преимуществам алгоритма HPA* можно отнести:
– простоту в реализации;
– не больше потребление памяти;
– скорость работы.
Недостатки:
– не учитывается разная проходимость карты.
А теперь используем данный алгоритм для движения робота по небольшому лабиринту, если нам известно строение лабиринта. Данный алгоритм может быть использован и в других различных проектах и разработках для движения различных объектов, например для движения сельхоз техники до поля, без участия водителя, по средствам GPS.
Рис. 2
Теперь встает новый вопрос: как посчитать длину ребра графа при известной карте местности?
Для этого нам понадобится алгоритм Ли, также известный как волновой алгоритм. Он может работать для поиска как ортогонального (4 направления перемещения робота), так и для ортогонально-диагонального (8 направлений перемещения робота) путей.
Работа алгоритма включает в себя три этапа: инициализацию, распространение волны и восстановление пути.
На этапе инициализации строится образ множества ячеек обрабатываемого поля, каждой ячейке приписываются атрибуты проходимости/непроходимости, обозначаются стартовая и финишная ячейки.
Далее, от стартовой ячейки порождается шаг в соседнюю ячейку, при этом проверяется, проходима ли она, и не принадлежит ли ранее меченной в пути ячейке.
При выполнении условий проходимости и непринадлежности её к ранее помеченным в пути ячейкам, в атрибут ячейки записывается число, равное количеству шагов от стартовой ячейки, от стартовой ячейки на первом шаге это будет 1. Каждая ячейка, меченая числом шагов от стартовой ячейки становится стартовой и из неё порождаются очередные шаги в соседние ячейки. Очевидно, что при таком переборе будет найден путь от начальной ячейки к конечной, либо очередной шаг из любой порождённой в пути ячейки будет невозможен.
Восстановление кратчайшего пути происходит в обратном направлении: при выборе ячейки от финишной ячейки к стартовой на каждом шаге выбирается ячейка, имеющая атрибут расстояния от стартовой на единицу меньше текущей ячейки. Таким образом находится кратчайший путь между парой заданных ячеек[3].
Для записи карты местности удобно использовать матричный массив. Каждый элемент матрицы будет обозначать 1 ячейку. Так мы можем не только точно оцифровать карту, но и задать дополнительные параметры для каждой клетки, а для удобства и координаты точки. В данном случае нам придется в качестве элементов использовать массивы. К примеру: (x, y, проходимость, тип (старт, финиш, промежуточная), число шагов).
После составления графа и нахождения оптимального пути, зная начальное положение робота, можно легко провести его по нему при помощи всего 2 датчиков поворота.
Заключение
В данной работе был разобран иерархический алгоритм поиска пути, отмечены его плюсы и минусы, а также способы его реализации.
Литература
- Дискретная математика: учебное пособие / А.В. Воронин. – Томск: Изд-во Томского Политехнического университета, 2009. – 116 с.
- Теория графов [Электронный ресурс] // Свободная энциклопедия «Википедия»
- Алгоритм Ли [Электронный ресурс] // Свободная энциклопедия «Википедия»
References
- Diskretnaja matematika: uchebnoe posobie / A.V. Voronin. – Tomsk: Izd-vo Tomskogo Politehnicheskogo universiteta, 2009. – 116 s.
- Teorija grafov [Jelektronnyj resurs] // Svobodnaja jenciklopedija «Vikipedija»
- Algoritm Li [Jelektronnyj resurs] // Svobodnaja jenciklopedija «Vikipedija»