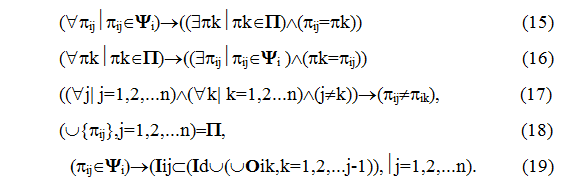ФОРМАЛЬНЫЙ МЕТОД ПРОВЕРКИ СВЯЗНОСТИ КОНТЕНТА ОБРАЗОВАТЕЛЬНОГО МОДУЛЯ
Ал Зирки М.М.
Ассистент кафедры Вычислительных Систем и Информационной Безопасности, Донской Государственный Технический Университет
ФОРМАЛЬНЫЙ МЕТОД ПРОВЕРКИ СВЯЗНОСТИ КОНТЕНТА ОБРАЗОВАТЕЛЬНОГО МОДУЛЯ
Аннотация
В статье рассмотрен формальный метод проверки логической связности учебных материалов учебно-методического комплекса модуля (дисциплины)образовательной программы направления высшего образования.
Ключевые слова: образовательная программа, модуль, дисциплина, логическая связность, образовательный контент.
Al Zirki M.M.
Assistant of department Computing Systems and Information Security, Don State Technical University
FORMAL METHOD OF COHERENCE CHECK CONTENT OF EDUCATION MODULE
Abstract
The article describes the formal method of checking logical coherence educational materials of educational- methodical complex (discipline) educational program directions of higher education.
Keywords: educational program, module, discipline, logical coherence, educational content.
Введение. Современные многоуровневые образовательные системы существенно опираются на информационные системы поддержки многоуровневого структурированного контента. Примерами такого контента в системе российского высшего образования (ВО) являются учебно-методические комплексы (УМК), на создание и поддержку в актуальном состоянии которых затрачиваются значительные усилия профессорско-преподавательского состава вузов. Каждый такой комплекс может содержать: рабочую программу модуля (дисциплины), Учебно-Методические Материалы (УММ), Контрольно-Измерительные Материалы (КИМы), различные нормативные материалы, методические и организационные рекомендации по технологии изучения модуля (дисциплины) и т.д. Каждая из групп материалов, образующих УМК, может содержать материалы, дифференцированные по формам обучения и уровням освоения учащимися модуля (дисциплины). Целью образования, согласно современной образовательной парадигме, является освоения обучающимися на достаточном уровне компетенций, заданных в компетентностной модели выпускника. Обучение реализуется с помощью современных образовательных технологий и связано, в том числе, с освоением обучающимися некоторого образовательного контента. В настоящее время все чаще под контентом подразумевают некоторый электронный образовательный контент. Структура и состав образовательного контента формируется в соответствии с Образовательной Программой (ОП) направления. Основными документами в ОП, определяющими контент, являются Учебный План (УП) направления и Учебно-Методические Комплексы (УМК). Рациональное проектирования как УП, так и УМК относится к сложному классу, так называемых, слабо структурированных задач. Процесс проектирования УП и УМК обычно содержит этап построения рациональной последовательности изучения элементов этих объектов. Для УМК эта задача сводится к решению проблемы выбора последовательности изучения элементов образовательного контента модуля (дисциплины). При этом важным является доказательство существование хотя бы одной логически связной последовательности изложения учебного материала. Модуль, образовательный контент которого обладает такой последовательностью, будем называть связным модулем. Следует отметить, что в известных научных исследованиях для решение проблемы связности, существующей и при проектировании УП, рекомендуется использовать неформальный механизм экспертных оценок. Решение же задачи о доказательстве связности модуля в настоящее время не рассматривалось. Отсутствие формального метода решения этой задачи тормозит исследование и развитие автоматизированных систем управления образовательным контентом.
Целью настоящей статьи является разработка формального метода решения задачи о связности модуля (дисциплины).
Аналитическая модель. В статье использован подход формализации ОП, изложенный в [1]. С точки зрения этого подхода целью изучения модуля ОП является освоение на заданном уровне логически связанных понятий и формирование определенных компетенций. Идентификаторы таких понятий будем называть термами. Изучаемые в модуле термы назовем выходными. Для их освоения студент должен владеть другими термами, которые будем называть входными. Множества входных и выходных термов задают на множестве модулей ОП отношение следования. Для реализации данного подхода на уровне модуля представим каждый модуль ОП как совокупность более простых дидактических единиц, каждая из которых так же обладает свойствами модульности. Для обозначения модулей, образующих ОП, введем понятие дисциплинарный модуль (d-модуль). Для обозначения модулей, образующих d-модуль, будем использовать термин «π-модуль» или подмодуль. При освоении каждого π-модуля так же осуществляется преобразование входных термов этого π-модуля в выходные. Таким образом, на множестве π-модулей, образующих данный d-модуль, существует отношение следования. В этом случае при проектировании d-модуля можно применить ту же модель, технологию и инструментальные средства, что и при проектировании ОП. Использование единого словаря термов для всех используемых в вузе ОП позволит связать между собой не только модули отдельной ОП, но модули различных образовательных программ.
Для ОП введем следующие обозначения:
P – образовательная программа (ОП);
S={s1,s2,...}; (1)
– множество обучающихся по программе P;
C={c1,c2,...ci,...cm}; (2)
– множество компетенций, осваиваемых студентами S по программе P;
T={t1,t2,…tk}; (3)
– множество термов, программы P;
TC={T1,T2,…Ti,…Tm}; (4)
– множество m подмножеств множества T;
Ec⊂C×TC; (5)
– бинарное отношение достаточности, для которого пара
(ci,Ti)∈Ec, (6)
если множество термов Ti, достаточно для описания компетенции ci;
Согласно рассмотренной в [1] модели ОП УМК является d-модулем, который представляет собой множество П={π1,π2,...,πn} p-модулей. С точки зрения организации образовательного процесса модуль πi – это часть УМК. В качестве примера такого модуля можно рассматривать раздел изучаемой дисциплины. В общем случае, каждый p-модуль может состоять из других, дочерних π-модулей. Модули, имеющие дочерние модули, будем называть сложными, а не имеющих дочерних — простыми. В данной статье, не уменьшая общности можно считать, что все модули из множества П={π1,π2,...,πn} являются простыми.
Для каждого модуля πi∈P зададим два множества термов Ii⊂T и Oi⊂T. Oi – множество выходных термов (понятий), которые изучаются в модуле πi. Ii – множество входных термов, которые необходимы обучающемуся для освоения в модуле πi термов Oi.
T - множество всех термов программы P.
Допустим, что в любом модуле всегда изучается хотя бы одно понятие. Следовательно:
Oi≠Ø, ∀i | i=1,2,...n. (7)
Обозначим через:
I=(∪Ii, где i=1,2,...n), (8)
– множество всех входных термов рассматриваемого d-модуля.
O=(∪Oi, где i=1,2,...n), (9)
– множество всех выходных термов рассматриваемого d-модуля.
Td=I∪O, (10)
– множество всех термов рассматриваемого d-модуля.
Очевидно, что мощность множества |Td|=k≥n, тогда:
Td={t1,t2,...,tk}, где tj∈T, j=1,2,...k. (11)
Определим множество Id входных термов d-модуля как разность между объединениями входных и выходных термов всех π-модулей из множества П={π1,π2,...,πn}:
Id=(I\O). (12)
Очевидно, что Id – это множество всех термов, которые не изучаются в d-модуле, но используются в нем. При этом, множество входных термов Id может быть пустым.
При изучении выходных термов p-модуля может потребоваться знание других термов. При этом можно говорить о некоторой «зависимости» выходных термов модуля от входных и формальной аналогии этой зависимости с понятием «функциональная зависимость» между атрибутами отношения в теории реляционных баз данных [2]. Эти зависимости используются при построении модели предметной области и являются результатом представления разработчика модели о семантике этой области.
Определение 1. Пусть дан модуль πi∈П, где П-множество π-модулей, образующих d-модуль. Ii и Oi – множества входных и выходных термов модуля πi соответственно. В этом случае будем говорить, что множество выходных термов (Oi) дидактически зависит от множества входных термов (Ii) и обозначать эту зависимость следующим образом:
πi:Ii⇒Oi (13)
Если существует дидактическая зависимость πi:Ii⇒Oi, то будем говорить, что множество Ii дидактически определяет множество Oi.
Важным свойством d-модуля является свойство связности.
Определение 2. Будем говорить, что d-модуль обладает свойством связности, если для его модулей из множества П={π1,π2,...,πn} существует такая упорядоченная последовательность изучения модулей множества П:
Yi=(pi1,pi2,...,pin), (14)
для которой выполняются следующие условия:
Иначе: d-модуль обладает свойством связности, если из всех его модулей можно составить такую последовательность Ψi, для любого модуля которой все входные теги изучались в предшествующих модулях, либо принадлежат множеству Id входных тегов d-модуля.
Определение 3. Последовательность (14), удовлетворяющая свойствам (15), (16), (17), (18), (19), будем называть допустимой последовательностью изучения d-модуля.
Определение 4. Множество всех тегов, которые могут быть изучены обучающимся в d-модуле, при условии, что ранее он освоил все входные теги этого модуля, будем называть замыканием входных тегов d-модуля и обозначать Id+.
Будем считать, что:
Id⊂Id+ (20)
Алгоритм построения замыкания входных тегов.
Дано:
П={π1,π2,...,πn} - множество простых π-модулей, образующих d-модуль.
Id – множество входных тегов d-модуля (30).
Ii и Oi – множества входных и выходных тегов модуля πi∈П соответственно.
Построить:
Id+ – замыкание множества Id.
Рассмотрим итерационный по множеству П алгоритм построения замыкания множества входных тегов d-модуля. Конечность множества П обеспечивает свойство конечности этого алгоритма. За начальное значение Id+ примем Id.
- Id+ := Id;
- ЧИСЛО_МОДУЛЕЙ:=n;
- СОЗДАТЬ ПУСТУЮ ПОСЛЕДОВАТЕЛЬНОСТЬ Ψ;
- ЦИКЛ_ПОКА ИСТИНА;
- i:=0;
- ФЛАГ_ОКОНЧАНИЯ:=ИСТИНА;
- ЦИКЛ_ПОКА i<ЧИСЛО_МОДУЛЕЙ;
- i:=i+1;
- ЕСЛИ (Ii ⊆ Id+) ∧ (Oi⊄ Id+) ТО
- Id+ := Id+ ∪ Oi ;
- ДОБАВИТЬ В ПОСЛЕДОВАТЕЛЬНОСТ Ψ МОДУЛЬ πi;
- ФЛАГ_ОКОНЧАНИЯ:=ЛОЖЬ;
- ВСЕ_ЕСЛИ;
- ВСЕ_ЦИКЛ;
- ЕСЛИ ФЛАГ_ОКОНЧАНИЯ ТО
- ПРЕРВАТЬ_ЦИКЛ;
- ВСЕ_ЕСЛИ;
18.ВСЕ_ЦИКЛ;
Представленный алгоритм работает таким образом, что при выполнении пункта 11 добавляемый в последовательность Ψ модуль πi и все ему предшествующие, могут быть изучены, при условии освоения обучающимся входных термов из множества Id до изучения d-модуля.
Алгоритм проверки d-модуля на связность.
Дано:
П={π1,π2,...,πn} - простые π-модули, образующие d-модуль.
Td – множество всех тегов d-модуля (27).
Id – множество входных тегов d-модуля (30).
Ii и Oi – множества входных и выходных тегов модуля πi∈П соответственно.
Проверить:
Свойство связности d-модуля.
Алгоритм проверки d-модуля на связность использует алгоритм построения замыкания множества входных тегов d-модуля;
- ПОСТРОИТЬ_МНОЖЕСТВО Id+ ;
- ЕСЛИ Td=Id+ ТО
- СВЯЗНОСТЬ_ МОДУЛЯ:=ИСТИНА;
- Ψ -ДОПУСТИМАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ МОДУЛЕЙ πi∈П;
- ИНАЧЕ
- СВЯЗНОСТЬ_МОДУЛЯ:=ЛОЖЬ;
- ВСЕ_ЕСЛИ;
При выполнении пункта 1 алгоритма проверки связности d-модуля строится множество Id+- замыкание множества входных термов этого модуля. При построении Id+ делается попытка построения Ψ - допустимой последовательности изучения всех p-модулей рассматриваемого d-модуля. В пункте 2 алгоритма проверяется условие, что множество всех термов d-модуля совпадает с замыканием его входных термов. Выполнение условия Td=Id+ означает, что все термы, изучение которых предполагалось в d-модуле, могут быть изучены. Выполнение условия (7) предполагает, что в каждом модуле из множества П={π1,π2,...,πn}, изучается хотя бы один терм. Следовательно, при выполнении условия Td=Id+ последовательность Ψ содержит все модули множества из П и является допустимой, а d-модуль обладает свойством связности.
Выводы. Предложенные в статье метод и алгоритмы позволяют формально проверять связность учебных материалов и могут быть использованы в автоматизированных системах управления образовательным контентом.
Литература
- Ал Зирки М.М., Гранков М.В. формализация критериев успешного освоения студентами образовательной программы // технические науки. вестник донского государственного технического университета.-2012 г. №3 (64).
- Дейт, К. Дж. Введение в системы баз данных, 8-е издание.: Пер. с англ. — М.: Издательский дом "Вильяме", 2005. — 1328 с.: ил. — Парал. тит. англ.
References
- Al Zirki M.M., Grankov M.V. formalizacija kriteriev uspeshnogo osvoenija studentami obrazovatel'noj programmy // tehnicheskie nauki. vestnik donskogo gosudarstvennogo tehnicheskogo universiteta.-2012 g. №3 (64).
- Dejt, K. Dzh. Vvedenie v sistemy baz dannyh, 8-e izdanie.: Per. s angl. — M.: Izdatel'skij dom "Vil'jame", 2005. — 1328 s.: il. — Paral. tit. angl.l.