Опубликовать статью Вход и регистрация
Расширенный поиск
Разделы статьи

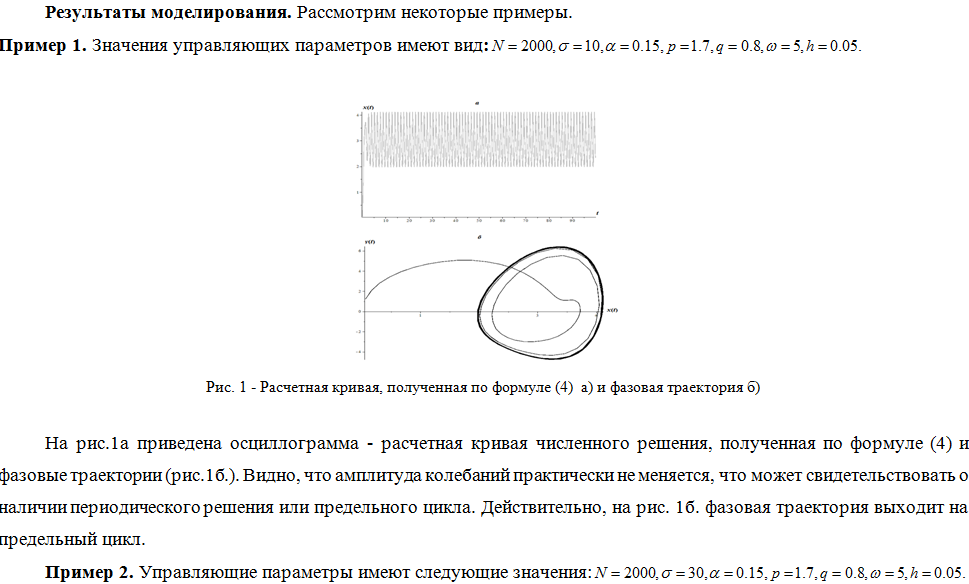
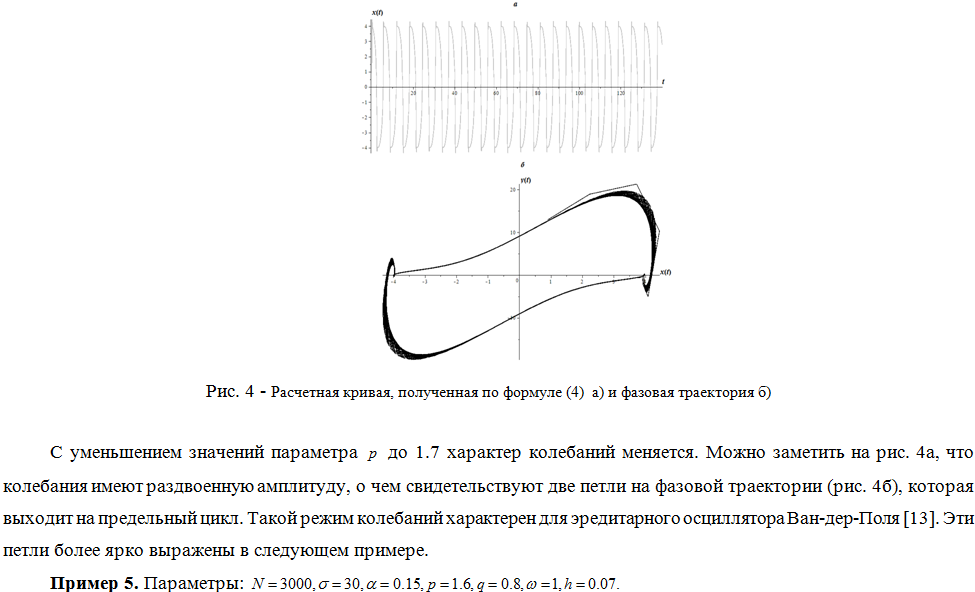
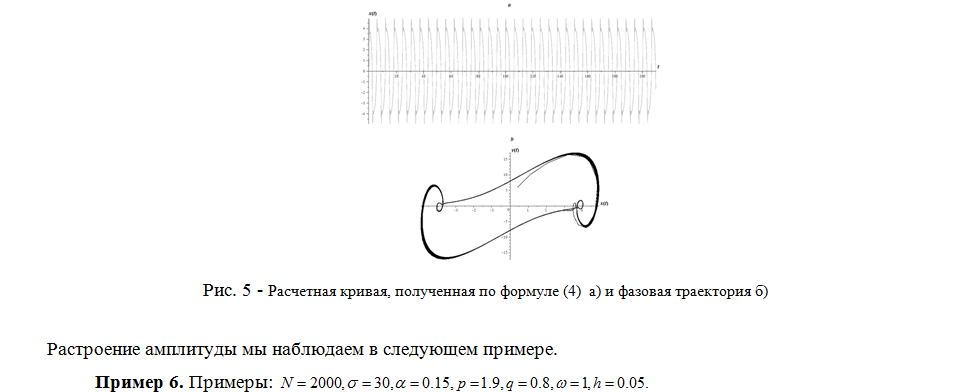
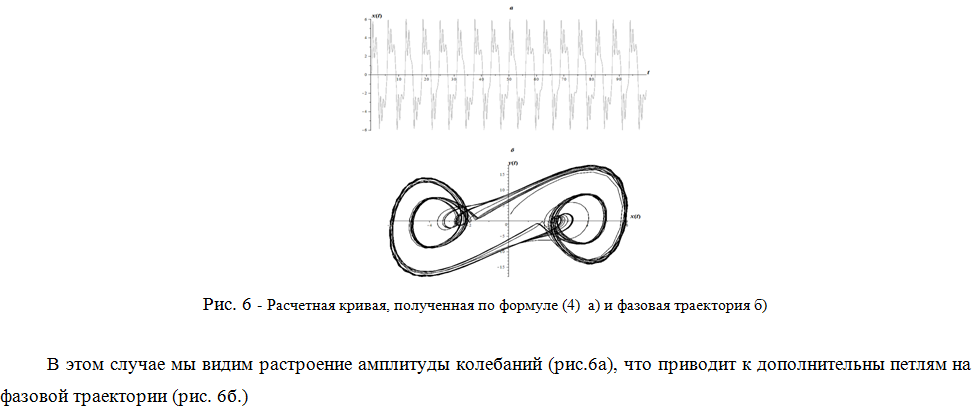
ЭРЕДИТАРНЫЙ ОСЦИЛЛЯТОР ДУФФИНГА С ЗАТУХАНИЕМ

Научная статья
Дробышева И.В.
Паровик Р.И.
DOI:
https://doi.org/10.18454/IRJ.2016.48.146
Выпуск: № 6 (48), 2016
Опубликована:
2016/06/17
PDF

Дробышева И.В.1, Паровик Р.И.2,3

1Студент-магистрант, 2ORCID: 0000-0002-1576-1860, Кандидат физико-математических наук, доцент, Камчатский государственный университет имени Витуса Беринга, 3Старший научный сотрудник, Институт космофизических исследований и распространения радиоволн ДВО РАН

ЭРЕДИТАРНЫЙ ОСЦИЛЛЯТОР ДУФФИНГА С ЗАТУХАНИЕМ

Аннотация

В работе предложена обобщенная математическая модель осциллятора Дуффинга с трением, которая учитывает эффект «памяти» или эредитарность в колебательной системе. Описание этого эффекта дается формальной заменой в модельном уравнении целочисленные производные на производные дробных порядков в смысле Римана-Лиувилля. Была построена явная конечно разностная схема для вычисления приближенного решения. Приведены примеры использования явной конечно-разностной схемы, в которых приведены осциллограммы и фазовые траектории, полученные при различных значениях управляющих параметров.

Ключевые слова: осциллятор Дуффинга, производная Римана-Лиувилля, конечно-разностная схема, фазовые траектории, осциллограммы.

Drobysheva I.V.1, Parovik R. I.2,3

1Undergraduate student , 2ORCID: 0000-0002-1576-1860, PhD in Physics and Mathematics, Associate professor, Vitus Bering Kamchatka State University, 3 Institute of Cosmophysical Research and Radio Wave Propagation FEB RAS

HEREDITARITY DUFFING OSCILLATOR WITH DAMPING

Abstract

The paper presents a generalized mathematical model of Duffing oscillator with friction that takes into account the effect of "memory" or hereditarity in an oscillatory system. The description of this effect is given formal change in the model equation integral derivatives on derivatives of fractional order in the sense of Riemann-Liouville. explicit finite difference scheme for calculating the approximate solution has been built. Examples of using explicit finite-difference scheme, which shows oscillograms and phase trajectories obtained for different values ​​of the control parameters.

Keywords: Duffing oscillator, Riemann-Liouville derivative, finite-difference scheme, phase trajectories, oscillograms.

16-06-2016 14-06-07

16-06-2016 14-08-48

16-06-2016 14-10-01

16-06-2016 14-13-23

16-06-2016 14-13-58

16-06-2016 14-15-55

16-06-2016 14-16-48

16-06-2016 14-17-38

16-06-2016 14-19-02

16-06-2016 14-20-03

Литература

  1. Учайкин В.В. Метод дробных производных. Ульяновск: Артишок, 2008. 512 с.
  2. Gao X., Yu J. Chaos in the fractional order periodically forced complex Duffing’s oscillators // Chaos, Solitons & Fractals. 2005. Т. 24. №. 4. С. 1097-1104.
  3. Rossikhin Y. A., Shitikova M. V. Application of fractional calculus for dynamic problems of solid mechanics: novel trends and recent results // Applied Mechanics Reviews. Т. 63. №. 1.  С. 010801.
  4. Petras I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation. New York: Springer, 2010.
  5. Syta A., Litak G., Lenci S., Scheffler M. Chaotic vibrations of the Duffing system with fractional damping // Chaos: An Interdisciplinary Journal of Nonlinear Science. 2014. Vol. 24, no. 1. P. 013107.
  6. Нахушев А.М. Дробное исчисление и его приложения. М.: Физматлит, 2003. 272 с.
  7. Марчук Г.И. Методы вычислительной математики. М.: Наука, 1977. 456 с.
  8. Паровик Р.И. О численном решении уравнения фрактального осциллятора с производной дробного переменного порядка от времени // Вестник КРАУНЦ. Физико-математические науки. 2014. №. 1 (8). C. 60-65.
  9. Паровик Р. И. Численный анализ некоторых осцилляционных уравнений с производной дробного порядка // Вестник КРАУНЦ. Физико-математические науки. 2014. №. 2 (9). C. 30-35.
  10. Паровик Р.И. Об одной конечно-разностной схеме для математической модели нелинейного эредитарного осциллятора // Международный научно-исследовательский журнал. 2016. № 4-2 (46). С. 138-142.
  11. Петухов А.А., Ревизников Д.Л. Алгоритмы численных решений дробно-дифференциальных уравнений // Вестник МАИ. 2009. Т. 16. № 6. С. 228-243.
  12. Паровик Р.И. Математическое моделирование нелокальной колебательной системы Дуффинга с фрактальным трением // Вестник КРАУНЦ. Физико-математические науки. 2015. №. 1 (10). C. 18-24.
  13. Паровик Р.И. Математическая модель фрактального осциллятора Ван дер Поля // Доклады Адыгской (Черкесской) Международной академии наук. 2015. Т.17. № 2. С. 57-62.
  14. Паровик Р.И. Об исследовании устойчивости эредитарного осциллятора Ван-дер-Поля // Фундаментальные исследования. 2016 №3(2). С. 283-287

References

  1. Uchajkin V.V. Metod drobnyh proizvodnyh. Ul'janovsk: Artishok, 2008. 510 s.
  2. Gao X., Yu J. Chaos in the fractional order periodically forced complex Duffing’s oscillators // Chaos, Solitons & Fractals. 2005. Т. 24. №. 4. С. 1097-1104.
  3. Rossikhin Y. A., Shitikova M. V. Application of fractional calculus for dynamic problems of solid mechanics: novel trends and recent results // Applied Mechanics Reviews. Т. 63. №. 1.  С. 010801.
  4. Petras I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation. New York: Springer, 2010.
  5. Syta A., Litak G., Lenci S., Scheffler M. Chaotic vibrations of the Duffing system with fractional damping // Chaos: An Interdisciplinary Journal of Nonlinear Science. 2014. Vol. 24, no. 1. P. 013107.
  6. Nahushev A.M. Drobnoe ischislenie i ego prilozhenija. M.: Fizmatlit, 2003. 272 s
  7. Marchuk G.I. Metody vychislitel'noj matematiki. M.: Nauka, 1977. 456 s.
  8. Parovik R.I. O chislennom reshenii uravnenija fraktal'nogo oscilljatora s proizvodnoj drobnogo peremennogo porjadka ot vremeni // Vestnik KRAUNC. Fiziko-matematicheskie nauki. 2014. 1(8). S. 60-65. DOI: 10.18454/2079-6641-2014-8-1-60-65.
  9. Parovik R.I. Numerical analysis some oscillation equations with fractional order derivatives// Bulletin KRASEC. Physical & Mathematical Sciences, 2014, 9:2, P. 34–38, DOI: 10.18454/2313-0156-2014-9-2-34-38.
  10. Parovik R.I. Ob odnoj konechno-raznostnoj sheme dlja matematicheskoj modeli nelinejnogo jereditarnogo oscilljatora // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal. 2016. № 4-2 (46). S. 138-142.
  11. Petuhov A.A., Reviznikov D.L. Algoritmy chislennyh reshenij drobno-differencial'nyh uravnenij // Vestnik MAI. 2009. T. 16. № 6. S. 228-243.
  12. Parovik R.I. Mathematical modeling of nonlocal oscillatory Duffing system with fractal friction// Bulletin KRASEC. Physical & Mathematical Sciences, 2015, 10:1, P. 16–21 DOI: 10.18454/10.18454/2313-0156-2015-10-1-16-21.
  13. Parovik R.I. Matematicheskaja model' fraktal'nogo oscilljatora Van der Polja // Doklady Adygskoj (Cherkesskoj) Mezhdunarodnoj akademii nauk. 2015. T.17. № 2. S. 57-62.
  14. Parovik R.I. Ob issledovanii ustojchivosti jereditarnogo oscilljatora Van-der-Polja // Fundamental'nye issledovanija. 2016 №3(2). S. 283-287.