Опубликовать статью Вход и регистрация
Расширенный поиск
Разделы статьи

БЕЗОПАСНОСТЬ ДАННЫХ НА ОСНОВЕ НЕЙРОННЫХ СЕТЕЙ

Научная статья
Кулиш А.В.
DOI:
https://doi.org/10.18454/IRJ.2016.54.178
Выпуск: № 12 (54), 2016
Опубликована:
2016/12/19
PDF

Кулиш А.В.

Аспирант, Санкт - Петербургский горный университет

БЕЗОПАСНОСТЬ ДАННЫХ НА ОСНОВЕ НЕЙРОННЫХ СЕТЕЙ

Аннотация

В этой работе предлагается система шифрования на основе искусственных нейронных сетей типа GRNN. Нейронная сеть используется для построения эффективной системы шифрования с использованием постоянно изменяющегося ключа. Нейронные сети предлагают очень мощную и общую структуру для представления нелинейного отображения из нескольких входных переменных для нескольких выходных переменных. Нейронную сеть можно рассматривать как подходящий выбор для функциональных форм, используемых для операций шифрования и дешифрования.

Ключевые слова: нейронная сеть, шифрование, дешифрование, ключ шифрования .

 

Kulish A.V.

Postgraduate student, Saint - Petersburg Mining University

DATA SECURITY BASED ON NEURAL NETWORKS

Abstract

In this paper, we propose an encryption system based on artificial neural networks GRNN type. A neural network is used to build an effective encryption system using a constantly changing key. Neural networks offer a very powerful and general framework for the non-linear mapping of multiple input variables for multiple output variables. The neural network can be considered as a suitable choice for functional forms that are used for encryption and decryption.

Keywords: neural network, encryption, decryption, encryption key.

 

  1. Введение

С появлением компьютера, возникла необходимость в автоматизированных инструментов для защиты файлов и другой информации, хранящейся на нем. Общим названием для инструментов, предназначенных для защиты данных и противодействию хакерам является компьютерная безопасность.

До сих пор наиболее важным инструментом для автоматизированной сетевой и коммуникационной безопасности является шифрование. Суть метода шифрования заключается в передаче данных в домен таким образом, чтобы сделать их устойчивыми к прослушиванию сети. Двумя основными методами, используемыми в области шифрования являются симметричное и асимметричное шифрование.

В симметричном шифровании, две стороны разделяют один ключ шифрования для расшифровки. Отправитель шифрует исходное сообщение (P), которое упоминается как простой текст, используя ключ (K), чтобы генерировать, по-видимому случайную бессмыслицу, упоминаемую как шифрованный текст (С), т.е.:

                                                                                          C =Encrypt(K,P).                                                                                         (1)

После того, как текст зашифрован , он может быть передан. После доставки шифрованный текст может быть преобразован обратно в исходный с помощью алгоритма дешифрования и того же ключа, который был использован для шифрования, который может быть выражен следующим образом:

                                                                                          P =Decrypt(K,C).                                                                                          (2)

В асимметричном шифровании используется два ключа, один ключ для шифрования и другой, парный ключ для дешифровки. Один из ключей является приватным и находится у стороны создавшей эту пару ключей, а другой обнародован. Теоретически, процесс шифрования реализован таким образом, что сообщение, зашифрованное с помощью открытого ключа, может быть расшифровано только соответствующим секретным ключом, в то время как сообщение, зашифрованное с помощью закрытого ключа, может быть расшифровано только с помощью соответствующего открытого ключа.

В этой статье представляется система шифрования на основе нейронных сетей (NNs). Нейронная сеть используется для построения эффективной системы шифрования с использованием постоянно изменяющегося ключа. Топология NN является важным вопросом, поскольку от этого зависит применение системы . Следовательно, так как приложение является проблемой вычисления, была использована многослойная топология. В настоящей работе, обобщённо-регрессионная нейронная сеть (GRNN), простая, однопараметрическая модель нейронной сети, предложенная для шифрования и дешифрования. Нейронные сети предлагают очень мощную и общую структуру для представления нелинейного отображения из нескольких входных переменных для нескольких выходных переменных. Процесс определения значений этих параметров на основе набора данных, упоминается как обучение или тренировка, и поэтому набор данных, как правило, называют обучающим множеством. Нейронную сеть можно рассматривать как подходящий выбор для функциональных форм, используемых для операций шифрования и дешифрования.

2. Дизайн предлагаемой системы

Функция шифрования состоит из следующих трех подфункций, описанных в следующих подразделах:

  1. ключи создаются;
  2. входное сообщение разбивается на блоки, равные количеству ключей и обрабатываются, один блок за один раз, в качестве входных данных для нейронной сети;
  3. нейронная сеть (GRNN) используется для шифрования каждого блока данных, продуцируя зашифрованное сообщение.

2.1. Создание ключей

Во-первых, необходимо выбрать супер-увеличение ранца(Knapsack) для шифрования данных. Число выбранных ключей, равно N, так что:

  1. сумма этих чисел (ключей) должны быть меньше 2х, где х = 2N, и
  2. числа не могут быть равны (K1 ≠ K2 ≠...≠ Kn ≠ 0)

        Для того, чтобы сохранить моделирование простым, были выбрали объекты со следующим номерами: 27, 14, 68, так что K1 = 27, K2 = 14 и K3 = 68 будут ключами.

2.2. Разбивая входные данные

        Предположим, что M представляет собой набор N-битовых начальных однополярных данных, т.е .:

                                                                                      Mi ={0,1},0 ≤ i ≤ N −1.                                                                                     (3)

В этой модели, 3-битный открытый текст вводится (N = 3) и 8-битный шифрованный текстовый выход (2N). Теперь нужно что-то зашифровать, например число 011010110. Во-первых, нужно разбить его на блоки (N = 3) длиной равной длине рюкзака, таким образом: 011 010 110. В первом блоке (011), есть 1-е, второе и третье места. Таким образом, берем второй и третий ключи и добавляем их друг к другу: 0 + 14 + 68 = 82. Повторение процедуры для всех блоков входных данных дает зашифрованную версию 01001000 , как это показано в таблице 1. Зашифрованные данные затем будут переданы получателю.

Таблица 1 – Полная структура учебных наборов данных

Вход Выход
P3 P2 P1 C1 C2 C3 C4 C5 C6 C7 C8
0 0 0 0 0 0 0 0 0 0 0
0 0 1 0 1 0 0 0 1 0 0
0 1 0 0 0 0 0 1 1 1 0
0 1 1 0 1 0 1 0 0 1 0
1 0 0 0 0 0 1 1 0 1 1
1 0 1 0 1 0 1 1 1 1 1
1 1 0 0 0 1 0 1 0 0 1
1 1 1 0 1 1 0 1 1 0 1

2.3. Предлагаемая система шифрования на основе нейронной сети

Нейронная сеть представляет собой структуру (сеть) состоящую из множества соединенных между собой звеньев (искусственных нейронов). Каждое звено имеет характерный ввод / вывод (I / O) и реализует локальное вычисление или функцию. Выход любого звена определяется характеристиками его ввода / вывода, его взаимосвязи с другими звеньями, а также внешними входами, если таковые имеются.

В данной работе GRNN простая, один параметр модели нейронной сети, предложен для шифрования и дешифрования.

Обобщённо-регрессионная нейронная сеть(GRNN) была разработана Шпехтом  и является простой, но очень эффективный локально приближенной, основанной на нейронной сети, в смысле оценки функции распределения вероятностей. Основные преимущества GRNN заключаются в следующем:

  • быстрое обучение;
  • сходимость к оптимальной регрессионной поверхности для большого количества образцов;
  • эффективное использование разреженных данных;
  • возможность обработки нестационарных данных.

GRNN использует стандартную статистическую формулу для расчета условного среднего Y скалярной случайной величины у дается измерение X векторной случайной величины х. Вектор случайной величины х соответствует входу сети и случайная y соответствует выходу сети. Помимо использования в качестве статического регрессионного метода, GRNN может использоваться, когда статистические данные изменяются с течением времени, используя полученные в последнее время, определяя постоянную времени и порога.

        Для того, чтобы построить GRNN:

  1. установить количество входного, промежуточного и выходного слоев (Processing Elements или PEs);
  2. выбрать промежуточные звенья;
  3. выбрать постоянную времени и фактор сброса;
  4. задать радиус влияния.

Это простой механизм кластеризации, который назначает входной вектор в кластере, если кластер центра это кластер центр ближайшего к входному вектору и ближе, чем радиус влияния. В противном случае, входной вектор назначается как центр нового кластера (если это возможно).

Реализация GRNN допускает экспоненциально убывающую σ следующего вида:

image001,                                                                                        (4)

где N это количество промежуточных звеньев, М число входных PEs и E должно лежать в диапазоне от 0 до 1.

2.4. Построение и обучение нейронной сети

Проблемной является вычислительная задача, поэтому будет использована многослойная GRNN. GRNN, используемая для шифрования состоит из трех слоев. Каждый слой состоит из ряда нейронов. В процессе шифрования, сообщение ввода делится на 3-битные наборы данных, в то время как 8-битные наборы производятся после процесса шифрования. Базовая архитектура GRNN показана на рисунке 1. Каждый слой состоит из следующих элементов:

  1. входной слой, состоящий из 3-х узлов, представляющий собой N-битные блоки;
  2. промежуточный слой из 8 узлов;
  3. выходной слой из 8 узлов, используемых для определения расшифрованного выходного сообщения.

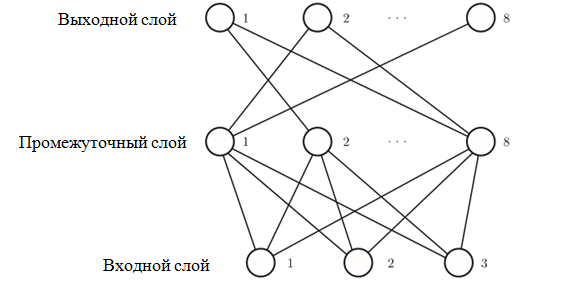
image002

Рис. 1 – Трехслойная архитектура GRNN

Остальные параметры GRNN:

  • временная постоянная = 1000.0;
  • фактор сброса = 0.000;
  • радиус влияния = 0.050;
  • σ scale=1.000;
  • σ exponent=0.500.

Значение 0.5 для E подходит в большинстве случаев. Значение 0.0 для E позволяет использовать постоянное значение для σ (равное 5).

Для изучения поведения NNS, используются два учебных комплекта:

  • полная схема входов, который состоит из всех возможных входных данных, или
  • половина схемы, упомянутой выше.

В начале обучения ключа шифрования, GRNN обеспечивается действительными состояниями, как показано в таблице 1, для полного образа и таблице 2, для половины входного образа. Обучающий набор повторно представляется к сети и весовые значения корректируются, пока общая ошибка не будет ниже заданного уровня толерантности. После того, как матрица весов построена, сеть проверяется на шифрование.

Таблица 2 – Полунаполненная структура наборов учебных данных

Вход Выход
P3 P2 P1 C1 C2 C3 C4 C5 C6 C7 C8
0 0 0 0 0 0 0 0 0 0 0
0 1 0 0 0 0 0 1 1 1 0
1 0 0 0 0 0 1 1 0 1 1
1 1 0 0 0 1 0 1 0 0 1

3. Результаты

Для того, чтобы оценить рассмотренный механизм, этапы шифрования типичных цифровых данных, показаны ниже. Протестировано поведение нейронной сети, описанной в предыдущем разделе, и обнаружено, что:

  1. нейронная сеть работает надежно при использовании полного образа и абсолютно никаких ошибок не обнаружено в выходах, как показано в таблице 3;
  2. производительность сети уменьшается при использовании только половины образа. Из-за многочисленных ошибок, обнаруженных в выходах, сеть не может зашифровать входные данные, как показано в таблице 4.
 

Таблица 3 – Результаты шифрования сети для полной образа входов

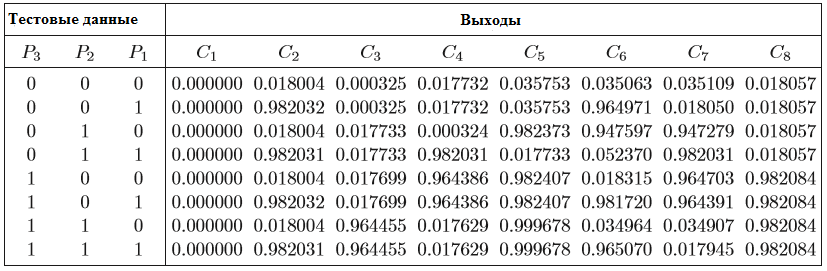
image003

Таблица 4 – Результаты шифрования сети для полунаполненного образа входов

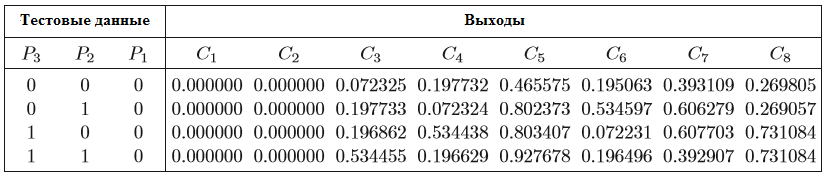
image004

В рамках испытаний было проведено исследование влияния числа скрытых блоков на модель конвергенции. Результаты этого исследования показаны на рисунке 2, на котором видно изменение ошибок в зависимости от количества нейронов в скрытом слое шифрования. Ошибки быстро уменьшаются до нуля при 8 скрытых нейронах, из чего следует, что число нейронов в скрытом слое должно быть равно числу нейронов в выходном слое.

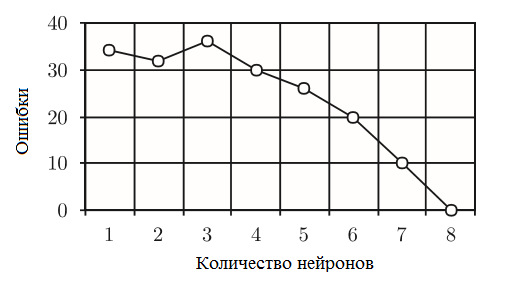
image005

Рис. 2 – Зависимость количества ошибок от количества нейронов

На приемном терминале, процесс дешифровки является обратным процессом шифрования. Для того, чтобы правильно расшифровывать шифровки данных:

  1. приемник должен использовать одни и те же номера ключей для расшифровки данных;
  2. данные должны достигнуть своего предполагаемого приемника, так как только приемник знает правильные номера ключей, необходимых для дешифрофки.

Сообщение должно быть подлинным, так как только отправитель имеет номера ключей, необходимых для шифрования сообщения, таким образом номера ключей приемника смогут расшифровать его правильно.

4. Заключение

Эта статья представляет собой попытку разработать систему шифрования на основе искусственных нейронных сетей типа GRNN, инвариантного к секретным ключам. Предлагаемый NN был испытан на различных учебных итерациях и для различного числа скрытых нейронов, входных данных. Результаты моделирования показали очень хороший результат, с относительно более высокой производительностью, чем традиционные методы шифрования.

Список литературы / References

  1. Stallings W. Data and Computer Communications / W. Stallings. – New Jersey, 2002. – 901 p.
  2. Tanenbaum A. Computer Networks / A. Tanenbaum. – Prentice Hall PTR, 1996. – 813 p.
  3. Stallings W. Cryptography and Network Security Principles and Practice / W. Stallings. – New Jersey, 2002 – 592 p.
  4. Specht D. F. IEEE Trans. Neural Networks 2 (6)/ D. F. Specht. – Kansas City, 1991 – 568 p.