АДАПТИВНЫЙ СЛУЧАЙНЫЙ ПОИСК В ЛОКАЛЬНЫХ И ГЛОБАЛЬНЫХ ЗАДАЧАХ ОПТИМИЗАЦИИ
АДАПТИВНЫЙ СЛУЧАЙНЫЙ ПОИСК В ЛОКАЛЬНЫХ И ГЛОБАЛЬНЫХ ЗАДАЧАХ ОПТИМИЗАЦИИ
Научная статья
Каладзе В.А.
Международный институт компьютерных технологий, Воронеж, Россия
Аннотация
Сформированные стратегии случайного поиска проводят адаптацию на уровне параметров рабочих шагов и стратегий пробного анализа. Они предназначены для поиска оптимума на сложных поверхностях в условиях информационной неопределённости.
Ключевые слова: случайный поиск, адаптация, направляющий конус.
Keywords: casual search, the adaptation, a directing cone.
Поставлена многомерная задача статистической поисковой минимизации [1] полиэкстремальной функции при наличии аддитивного шума. В таких задачах функция цели относится к классу глобально-унимодальных функций, огибающие которых унимодальны. Для поиска на произвольных полимодальных поверхностях используются генетические алгоритмы, также относящиеся к процедурам случайного поиска.
Функция цели Q(x1, …, xn) поиска определяется как выпуклый функционал, отображающий допустимую область (x1, …, xn) Î D на множество неотрицательных чисел. Это позволяет использовать в случайном поиске для характеризации точек минимума функционала, заданного на множестве нормированного векторного пространства, конуса допустимых направлений [2, 3], выпуклых подмножеств множества D, когда точка минимума связывается с пустотой пересечения конусов.
Развивая принцип [1] направляющего конуса в случайном поиске, разработаны стратегии пошаговой адаптации направления поиска путём подбора текущего множества пробного анализа и оценки характеристик рабочего шага, удовлетворяющего условию локального улучшения.
Адаптация связана с оценкой варьируемого n-мерного вектора 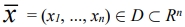 минимизирующей поисковой процедуры
минимизирующей поисковой процедуры
 (1)
(1)
в условиях информационной неопределённости.
В случайном поиске для выбора направления движения к цели, определяемой критерием эффективности, используются генерации вектора 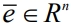 – случайного n-мерного вектора единичной длины, определяемого плотностью распределения
– случайного n-мерного вектора единичной длины, определяемого плотностью распределения 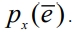 Решающая
Решающая 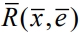 функция процедуры (1) связывает направление рабочего шага
функция процедуры (1) связывает направление рабочего шага 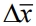 и его величину, устанавливаемую многомерным числовым оператором A, через соотношение
и его величину, устанавливаемую многомерным числовым оператором A, через соотношение 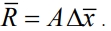
Для реализации адаптивных свойств поиска параметризуется распределение вероятности 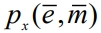 выбора пробного шага включением настраиваемого n-мерного вектора
выбора пробного шага включением настраиваемого n-мерного вектора  осевого направления конуса с вершиной в
осевого направления конуса с вершиной в 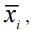 который содержит направления пробных шагов и определяет направление рабочего шага поиска
который содержит направления пробных шагов и определяет направление рабочего шага поиска 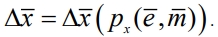
Адаптация поисковой процедуры сводится к численной аппроксимации закона распределения в текущей точке поиска на случайном множестве пробного анализа. Направление (i + 1)-го рабочего шага процедуры адаптивного случайного поиска (АСП) определяется по результатам 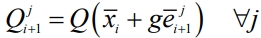 q случайных пробных шагов
q случайных пробных шагов 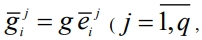 g = const), выполненных в текущей точке
g = const), выполненных в текущей точке 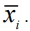
В [4] на основе прямого и обратного уравнений Колмогорова показана закономерность использования функции плотности вероятности для адаптации процедуры случайного поиска. Её первый начальный момент определяется по наилучшей пробе, как модальное значение нормированной целевой функции. Второй момент распределения оценивается отклонением относительно этого вектора границ вершинного угла φ, формируемого через min и max углов направляющих косинусов векторов памяти Mi p.
Вектор 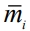 в момент времени i определяется по результатам текущего пробного анализа, представленного модальным вектором
в момент времени i определяется по результатам текущего пробного анализа, представленного модальным вектором 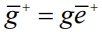 , и с учётом
, и с учётом 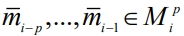 – значений вектора
– значений вектора  на предыдущих шагах, где p – глубина адаптивной памяти случайного поиска (p < n).
на предыдущих шагах, где p – глубина адаптивной памяти случайного поиска (p < n).
Наличие помех добавляет определённый консерватизм в локальную пошаговую стратегию поиска. Вектор 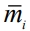 формируется как средневзвешенная сумма вектора
формируется как средневзвешенная сумма вектора  и векторов памяти Mi p, состоящих из векторов направлений предыдущих рабочих шагов поиска:
и векторов памяти Mi p, состоящих из векторов направлений предыдущих рабочих шагов поиска:
− при высоком уровне помех
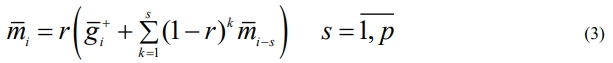
− при невысокой интенсивности шума

Рассчитаны [4] условия переключений локальной и глобальной стратегий поиска. Если невозможно выбрать наилучшее направление поиска, то проверяется экстремальность найденной точки по условию пустоты пересечения множества конусов направлений в ней.
Процедура АСП в окрестности оптимума проводится как стохастическая аппроксимация Кифера-Вольфовица. Величина угла φ конуса в локальных стратегиях не превышает π/2, что следует из условия локального улучшения. При этом связь между углом φ и величинами шагов поиска отсутствует. В глобальных стратегиях величина φ, изменяющаяся от π/2 до π по требованию критерия оптимальности, определяет значение шага глобального поиска
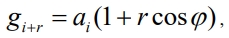
как пробного, так и рабочего: 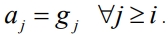
Экспериментальные исследования, в которых кроме известных функций Rosenbrock’s и Rastrigin’s использовалась при k = 5 разработанная тестовая функция Caterina’s
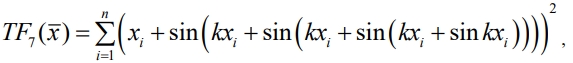
подтвердили работоспособность алгоритма, его эффективность в условиях глобально-унимодальной функции и функции с овражным рельефом дна, что значительно усложняет поиск экстремума, находящегося на «дне оврага», поскольку регулярные локальные технологии здесь теряют свою эффективность, а глобальные – выводят точку поиска из зоны экстремума.
Список литературы / References
- Растригин Л.А. Статистические методы поиска. М.: Наука, 1968. 376 с.
- Красносельский М.А. Позитивные линейные системы: метод положительных операторов/ М.А. Красносельский, Е.А. Лифшиц, А.В. Соболев. – М.: Наука, 1985. – 256 с.
- P.-J. Laurent. Approximation et optimization. Paris, Hermann, 1972. 496 p. (рус. перевод: П.-Ж. Лоран. Аппроксимация и оптимизация. – М.: Мир, 1975. – 496 с.)
- Kaladze V.A. Mathematical models of casual processes with stationary increments and the non-uniform information dynamic processing: Monograph. –Lorman,MS,USA: Science Book Publishing House, 2012. – 136 p.
