МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ КИНЕТИКИ ВЛАЖНОСТИ ЗЕРНА ОЗИМОЙ ПШЕНИЦЫ В ПРОЦЕССЕ СУШКИ
DOI: https://doi.org/10.23670/IRJ.2022.118.4.008
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ КИНЕТИКИ ВЛАЖНОСТИ ЗЕРНА ОЗИМОЙ ПШЕНИЦЫ В ПРОЦЕССЕ СУШКИ
Научная статья
Дарманян А.П.1,*, Богданов С.И.2, Маркин М.А.3
1 ORCID: 0000-0002-1956-9892;
2 ORCID: 0000-0002-3111-2895;
1, 2, 3 Волгоградский государственный аграрный университет, Волгоград, Россия
* Корреспондирующий автор (A.Darmanyan[at]volgau.com)
Аннотация
В работе приведены результаты лабораторных экспериментальных исследований изменения влажности зерна озимой пшеницы W от времени t(сек) в процессе сушки при двух значениях начальной влажности W0 (24% и 17,5%), в диапазоне температур сушки 100ОС-160ОС с интервалом 20ОС. Средствами ПП Statistica 6.0 с помощью множественного регрессионного анализа найдена математическая модель для описания кинетики сушки зерна озимой пшеницы в виде трехпараметрической двухфакторной модели W/W0 = a0 + a1*t + a2*t2 +𝛆, статистическая значимость которой подтверждена высокими значениями коэффициента детерминации при всех исследованных режимов сушки в диапазоне 0,993-0,997 и значениями критерия Фишера. Определены параметры найденной математической модели для всех исследованных технологических режимов и выполнено сравнение расчетных значений влажности зерна в различные моменты времени с реальными значениями.
Ключевые слова: озимая пшеница, сушказерна, влажность, моделирование, регрессионный анализ.
MATHEMATICAL MODELING OF WINTER WHEAT GRAIN MOISTURE KINETICS DURING DRYING
Research article
Darmanyan A.P.1,*, Bogdanov S.I.2, Markin M.A.3
1ORCID: 0000-0002-1956-9892;
2ORCID: 0000-0002-3111-2895;
1, 2, 3 Volgograd State Agrarian University,Volgograd, Russia
* Corresponding author (A.Darmanyan[at]volgau.com )
Abstract
The paper presents the results of laboratory experimental studies of changes in the moisture content of winter wheat grain W from time t (sec) during drying at two values of initial humidity W 0 (24% and 17.5%), in the drying temperature range of 100 OС – 160 OС with an interval of 20OС. By means of Statistica 6.0, using multiple regression analysis, a mathematical model was found to describe the kinetics of drying winter wheat grain in the form of a three-parameter two-factor model W/ W 0 = a0 + a1*t + a2*t 2 +𝛆, the statistical significance of which is confirmed by high values of the coefficient of determination for all drying modes under study in the range 0.993-0.997 and values of the Fisher criterion. The article determines the parameters of the found mathematical model for all the technological modes under study and compares the calculated values of grain moisture at various points in time with real values.
Keywords: winter wheat, grain drying, humidity, modeling, regression analysis.
Введение
Важным этапом послеуборочной обработки зерновых культур является процесс сушки зерна, в котором зерно высушивают от начальной влажности W0 = (17 – 26)% до кондиционного значения = (13 – 14)%, которое регламентировано ГОСТом [1]. Известны результаты экспериментальных исследований процесса сушки зерна, которые были проведены на различных зерновых культурах таких, как амарант [2] и ячмень [3] с использованием разнообразных конструкций сушилок и при различных технологических условиях [3], [4], [5]. В результате экспериментальных исследований процесса сушки зерна в конкретных сушилках, а также в результате математического моделирования самого процесса сушки зерна были предложены различные регрессионные модели [4], [6], [7] для описания кинетики сушки зерна в виде временной зависимости влажности зерна. Однако зачастую такие модели представляют сложные нелинейные регрессионные зависимости, параметрами которых являются многочисленные технологические условия и конструктивные особенности проведения процесса сушки [3], [4], [5], [6].
В тоже время для расчета размеров сушильных установок и определения их производительности необходимо иметь математическую модель, которая описывала бы сам процесс сушки зерна как временной процесс изменения влажности зерна от начального состояния до кондиционного значения под воздействием температуры, т.е. необходима математическая модель кинетики сушки. И особенно это важно для такой широко распространенной зерновой культуры, как зерно озимой пшеницы. На наш взгляд, одной из причин отсутствия приемлемой для расчетов сушильного оборудования математической модели сушки зерна озимой пшеницы является неэффективное использование прикладных статистических методов для обработки экспериментальных данных [8], [9].
Цель исследования
Экспериментальное исследование процесса сушки зерна озимой пшеницы и формирование на основе этих исследований математической модели для описания кинетики влажности зерна в зависимости от температуры сушки и его начальной влажности.
Методы исследования
Эксперименты проводились на лабораторной установке с использованием влагомера весовой серии МХ-50 [10]. В экспериментах использовалось зерно озимой пшеницы, выращенное в хозяйстве УНПЦ «Горная поляна» (г. Волгоград), которое имело следующие характеристики: начальная влажность W0 = 17,5% и 24%, содержание клейковины 31,2; качество клейковины (ИДК) 102; содержание белка 17,8%. Зерно в количестве 15г подвергалось сушке при температуре Tот 100 ОС до 160 ОС с интервалом 20 ОС. В соответствии с рекомендациями [11] методика проведения экспериментов заключалась в следующем. Сначала с помощью весов отвешивалось 15 грамм увлажненного зерна, выбиралась встроенная в прибор МХ-50 программа для сушки зерна, затем при условии поддержания выбранного температурного режима измерялась влажность зерна в зависимости от текущего времени t (сек). Экспериментальные исследования проводились при температуре окружающей среды 23℃ и относительной влажности воздуха 48%. В каждом эксперименте влажность зерна измерялась через постоянные интервалы времени (t = 10 сек), в результате чего были получены кинетические кривые влажности зерна в виде W =f(t) для каждой температуры Tи для каждого значения начальной влажности (W0 = 18% и 24%).
Основные результаты
Для проведения математического моделирования полученные экспериментальные кинетические кривые были преобразованы в безразмерный вид W/W0 =f(t), гдеW0 – начальная влажность.
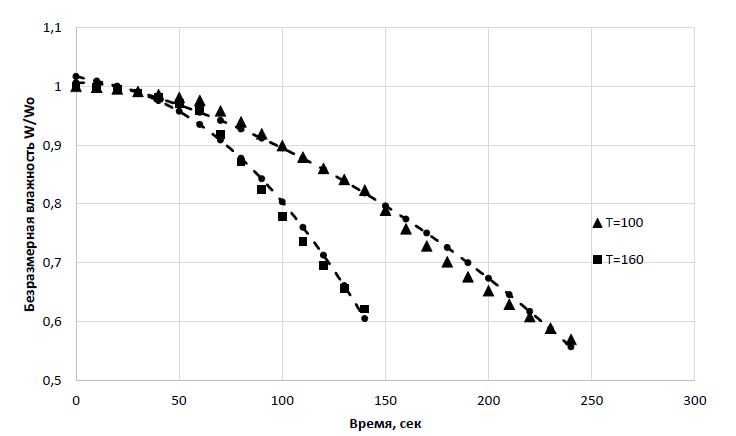
Рис. 1 – Кинетические кривые влажности зерна озимой пшеницы с начальной влажностью 24% при различных температурах: пунктирные линии – регрессионная модель (1) с параметрами из таблицы 1
На рис.1 показаны безразмерные кинетические кривые влажности зерна с начальной влажностью 24% при двух значениях температуры сушки (100ОС и 160ОС), а на рис.2 – для зерна с начальной влажностью 17,5% при тех же значениях температуры. Общий вид полученных нами кинетических кривых соответствует таким же кинетическим кривым, которые приведены в работах [2], [7]. Как видно из полученных временных закономерностей (см.рис.1 и рис.2) изменение влажности зерна озимой пшеницы в процессе сушки — это сложный нелинейный процесс во времени.
Для поиска математической модели, которая могла бы описать такие нелинейные закономерности, в качестве инструментария был использован множественный регрессионный анализ в среде ПП Statistica 6.0 [12], причем в качестве математической модели была выбрана следующая трехпараметрическая двухфакторная модель:
| |
(1) |
где t – время (сек), W0 –начальная влажность (%), a0, a1иa2-параметры модели,𝛆 – случайная величина.
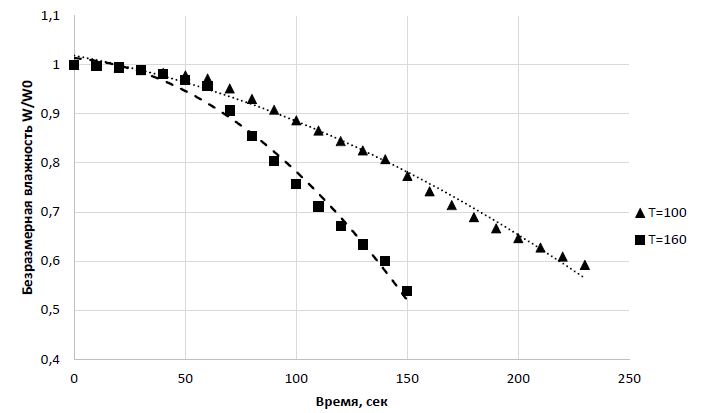
Рис. 2 – Кинетические кривые сушки зерна озимой пшеницы с начальной влажностью 17,5% при различных температурах: пунктирные линии– регрессионная модель (1) с параметрами из таблицы 2
Результаты множественного регрессионного анализа для зерна с начальной влажностью 24% приведены в таблице 1, а для зерна с начальной влажностью 17,5% - в таблице 2.
Таблица 1 – Результаты множественного регрессионного анализа кинетики влажности зерна озимой пшеницы с начальной влажностью 24%
| Температура сушки,ОС | Параметры модели (1) | Коэффициент детерминации | ||
| a0 | a1 | a2 | ||
| 100 | 1,01666 | -0,000716 | -0,000005 | 0,994 |
| 120 | 1,00642 | -0,000076 | -0,000016 | 0,997 |
| 140 | 1,00646 | -0,000077 | -0,000016 | 0,997 |
| 160 | 1,00609 | 0,000075 | -0,000021 | 0,996 |
Таблица 2 – Результаты множественного регрессионного анализакинетики влажности зерна озимой пшеницы с начальной влажностью 17,5%
| Температура сушки, ОС | Параметры модели (1) | Коэффициент детерминации | ||
| a0 | a1 | a2 | ||
| 100 | 1,018954 | -0,000850 | -0,000005 | 0,993 |
| 120 | 1,005621 | -0,000185 | -0,000013 | 0,994 |
| 140 | 1,010694 | -0,000365 | -0,000016 | 0,995 |
| 160 | 1,013766 | 0,000362 | -0,000020 | 0,996 |
Обсуждение
Как видно из полученных значений в таблицах 1 и 2, для всех значений температуры сушки в интервале 100-160ОС коэффициент детерминации имеет очень высокое значение 0,993-0,997, а значения критерия Фишера во всех экспериментах находились в интервале 9600-40900, что подтверждает статистическую значимость самой математической модели (1). Кроме того, в результате расчетов параметров модели (1) было установлено, что для всех значений температур и для двух значений начальной влажности (17,5% и 24%) все параметры модели (1) a0, a1иa2 статистически значимы на уровне р=0,05. Все это является доказательством того, что найденная математическая модель (1) со значениями параметров в таблицах 1 и 2 адекватно описывает экспериментальные данные по кинетике сушки зерна озимой пшеницы.
На рис.1 и рис.2 пунктирной линией показаны значения влажности зерна W/W0, вычисленные с помощью математической модели (1) и со значениями параметров a0, a1иa2 из таблиц 1 и 2. Как видно, расчетные значения хорошо соответствуют реальным данным, что свидетельствует о хорошей аппроксимирующей способности найденной модели (1) и значений ее параметров a0, a1иa2, приведенных в таблице 1 и в таблице 2.
Для проверки прогнозных качеств найденной математической модели в качестве примера были выполнены расчеты текущей влажности зерна в процессе сушки для зерна с начальной влажностью W0=17,5% при температуре сушки T = 120 ОС по выражению (1), которое для данных условий согласно значениям параметров в таблице 2 имеет следующий вид:
| |
(2) |
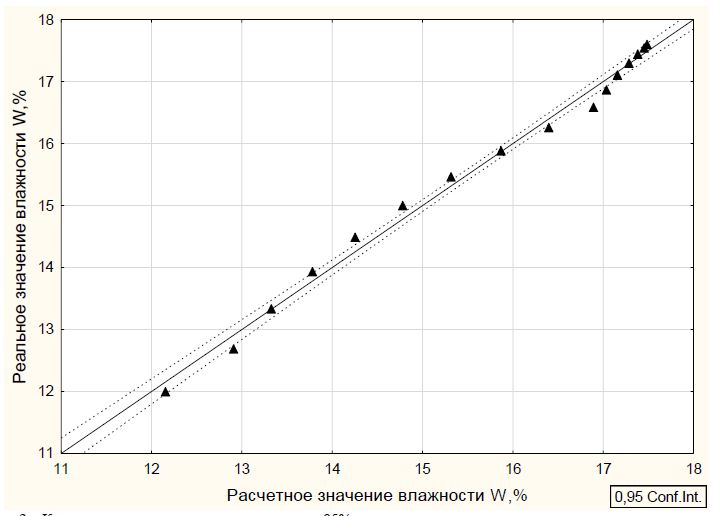
Результаты расчетов текущей влажности зерна W,% по выражению (2) средствами ПП Statistica 6.0 [12] представлены на рис.3 в сравнении с экспериментально измеренными значениями влажности зерна W,% вместе с 95% доверительными интервалами.
Рис. 3 – Корреляционное поле и линия регрессии с 95% -доверительным интервалом для расчетного и реального значений влажности зерна озимой пшеницы в процессе сушки при температуре 120 ОС
Из рисунка 3 ясно видно, что имеет место хорошее соответствие вычисленных значений влажности зерна с экспериментально измеренными значениями влажности зерна (см.линейную зависимость на рис.3) на уровне значимости 0,05 (95% -доверительный интервал).
Полученные математические модели (см. таблицы 1 и 2) могут быть использованы для вычисления времени сушки зерна озимой пшеницы от начальной влажности до конечной влажности , что позволит определять производительность установки при заданном объеме зерна.
Заключение
Выполнены экспериментальные исследования изменения влажности зерна озимой пшеницы во времени в процессе сушки при двух значениях начальной влажности (12% и 17,5%) и в диапазоне температур сушки (100 ОС-160ОС). С помощью множественного регрессионного анализа средствами ПП Statistica 6.0 найдена математическая модель для описания кинетики сушки зерна озимой пшеницы в виде трехпараметрической двухфакторной модели W/W0 = a0 + a1*t + a2*t2 +𝛆, адекватность которой подтверждена высокими значениями коэффициентов детерминации и критерия Фишера. Определены параметры этой модели для всех исследованных режимов, которые оказались статистически значимы на уровне р=0,05. Проведено сравнение расчетных значений влажности зерна в различные моменты времени с реальными значениями, в результате которого показано хорошее соответствие на уровне значимости 0,05 (95% -доверительный интервал).
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы/References
- ГОСТ Р 55262-2012. Сушильные машины и установки сельскохозяйственного назначения. Методы испытаний. – Введ. 2014-01-01. – М.: Изд-во стандартов, 2015. – 127 с.
- Станкевич Г.Н. Исследование кинетики сушки зерна амаранта / Г. Н. Станкевич, Н. А. Валентюк // Актуальные проблемы сушки и термовлажностной обработки материалов в различных отраслях промышленности и агропромышленном комплексе : сборник научных статей Первых Международных Лыковских научных чтений, посвящённых 105-летию академика А.В. Лыкова, Москва, 22–23 сентября 2015 года. – Москва: ЗАО "Университетская книга", 2015. – С. 244-246.
- Масалимов И. Х. Математическая модель сушки зерна ячменя инфракрасным нагревом в вакууме / И. Х. Масалимов, Х. Т. Каримов, В. А. Павленко // Инновации в сельском хозяйстве. – 2019. – № 3(32). – С. 95-101.
- Пахомов В. И. Регрессионная математическая модель двухэтапной комбинированной электротехнологии высокотемпературной конвективной сушки и озоновоздушной обработки зерна / В. И. Пахомов, В. С. Газалов, К. Н. Буханцов // Тракторы и сельхозмашины. – 2019. – № 1. – С. 81-95.
- ШуракА.А.Исследование влияния геометрических характеристик аппаратов с псевдоожиженным слоем на технологические параметры процесса сушки / А.А. Шурак, А.А. Шагарова, Л.М. Мансур // Технологии нефти и газа.– 2020. – № 6 (131). –C. 50-53.
- Рогачев А.Ф. Математическое моделирование процесса послеуборочной сушки зерна / А.Ф. Рогачев, Д. В. Шатырко // Известия Нижневолжского агроуниверситетского комплекса: Наука и высшее профессиональное образование. – 2015. – № 4(40). – С. 168-174.
- Малин Н.И. Моделирование кинетики двухступенчатой прямоточной сушки зерна / Н. И. Малин // Евразийский союз ученых. – 2019. – № 12-5(69). – С. 11-16.
- Дарманян А.П. Научная значимость статистических методов анализа экспериментальных данных в системе послевузовского аграрного образования/А.П. Дарманян, Н.М. Веселова. // Актуальные вопросы профессионального образования. – 2018. – № 3(12). – С.33-37.
- Darmanyan A. P. Modeling potato yield statistics by using information technology for sustainable development / A. P. Darmanyan and S. I. Bogdanov // 2022 IOP Conf. Ser.: Earth Environ. Sci. 965 012058. – [Electronic resource]. URL: https://iopscience.iop.org /article/10.1088/1755-1315/965/1/012058 (accessed 06.03.2022).
- Влагомер весовой серии MS, MX, MF, ML. Руководство по эксплуатации. Технический паспорт. – [Электронный ресурс]. URL: https://clck.ru/et7sD (дата обращения 06.03.2022).
- Инструкция по сушке продовольственного, кормового зерна, маслосемян и эксплуатации зерносушилок №9-3-82. -М.: ЦНИИТЭИ Мингаза СССР, 1982. – 61с.
- Куприенко Н.В. Статистические методы изучения связей. Корреляционно-регрессионный анализ/Н. В. Куприенко, О.А. Пономарева, Д.В Тихонов. – СПб.: Изд-во политехн. ун-та,2008. – 118 с.
Список литературы на английском языке/ References in English
- GOST R 55262-2012. Sushilnyye mashiny i ustanovki selskokhozyaystvennogo naznacheniya. [Drying machines and installations for agricultural purposes. Test methods]. – Input. 2014-01-01. – M.: Publishing house of standards, 2015. – 127 p.[in Russian]
- Stankevich G.N. Issledovaniye kinetiki sushki zerna amaranta [Study of the kinetics of drying amaranth grain]. / N. Stankevich, N. A. Valentyuk // Aktualnyye problemy sushki i termovlazhnostnoy obrabotki materialov v razlichnykh otraslyakh promyshlennosti i agropromyshlennom komplekse : sbornik nauchnykh statey Pervykh Mezhdunarodnykh Lykovskikh nauchnykh chteniy. posvyashchennykh 105-letiyu akademika A.V. Lykova. Moskva. 22–23 sentyabrya 2015 goda. [Actual problems of drying and thermal and moisture treatment of materials in various industries and agro-industrial complex: a collection of scientific articles of the First International Lykovsky Scientific Readings dedicated to the 105th anniversary of Academician A.V. Lykova, Moscow, September 22–23, 2015. – Moscow: CJSC "Universitetskaya kniga", 2015]. – pp. 244-246. [in Russian]
- Masalimov I.Kh. Matematicheskaya model sushki zerna yachmenya infrakrasnym nagrevom v vakuume [Mathematical model of barley grain drying by infrared heating in vacuum]. / I. Kh. Masalimov, Kh. T. Karimov, V. A. Pavlenko // Innovatsii v selskom khozyaystve [Innovations in agriculture]. – 2019. – No. 3 (32). – pp. 95-101. [in Russian]
- Pakhomov V.I. Regressionnaya matematicheskaya model dvukhetapnoy kombinirovannoy elektrotekhnologii vysokotemperaturnoy konvektivnoy sushki i ozonovozdushnoy obrabotki zerna [Regression mathematical model of two-stage combined electrotechnology of high-temperature convective drying and ozone-air grain processing]. / V. I. Pakhomov, S. Gazalov, K. N. Bukhantsov / Traktory i selkhozmashiny [Tractors and agricultural machines]. – 2019. – No. 1. – P. 81-95. [in Russian]
- Shurak A.A. Issledovaniye vliyaniya geometricheskikh kharakteristik apparatov s psevdoozhizhennym sloyem na tekhnologicheskiye parametry protsessa sushki [Investigation of the influence of the geometric characteristics of apparatuses with a fluidized bed on the technological parameters of the drying process] / A.A. Shurak, A.A. Shagarova, L.M. Mansur // Tekhnologii nefti i gaza [Technologies of oil and gas]. – 2020. – No. 6 (131). –pp. 50-53. [in Russian]
- Rogachev A.F. Matematicheskoye modelirovaniye protsessa posleuborochnoy sushki zerna [Mathematical modeling of the process of post-harvest drying of grain]. / A.F. Rogachev, D.V. Shatyrko // Izvestiya Nizhnevolzhskogo agrouniversitetskogo kompleksa: Nauka i vyssheye professionalnoye obrazovaniye [Proceedings of the Nizhnevolzhsky agro-university complex: Science and higher professional education]. – 2015. – No. 4 (40). – pp. 168-174. [in Russian]
- Malin N.I. Modelirovaniye kinetiki dvukhstupenchatoy pryamotochnoy sushki zerna [Modeling the kinetics of two-stage direct-flow drying of grain]. / N. I. Malin // Evraziyskiy soyuz uchenykh [Eurasian Union of Scientists]. – 2019. – No. 12-5 (69). – P. 11-16. [in Russian]
- Darmanyan A.P.Nauchnaya znachimost statisticheskikh metodov analiza eksperimentalnykh dannykh v sisteme poslevuzovskogo agrarnogo obrazovaniya[Scientific significance of statistical methods for the analysis of experimental data in the system of postgraduate agricultural education]. / A. P. Darmanyan, N. M. Veselov // Aktualnyye voprosy professionalnogo obrazovaniya [Topical issues of vocational education].– 2018. – No. 3 (12). – pp.33-37. [in Russian]
- Darmanyan A. P. Modeling potato yield statistics by using information technology for sustainable development / P. Darmanyan and S. I. Bogdanov // 2022 IOP Conf. Ser.: Earth Environ. Sci. 965 012058. – [Electronic resource]. URL: https://iopscience.iop.org /article/10.1088/1755-1315/965/1/012058 (accessed 06.03.2022).
- Moisture meter for weight series MS, MX, MF, ML. Manual. Technical certificate. – URL: https://clck.ru/et7sD (accessed 03/06/2022). [in Russian]
- Instructions for drying food, feed grains, oilseeds and operation of grain dryers No. 9-3-82. – M.: TsNIITEI Mingaz USSR, 1982. – 61p. [in Russian]
- Kuprienko N.V. Statisticheskiye metody izucheniya svyazey. Korrelyatsionno-regressionnyy analiz [Statistical methods for studying relationships. Correlation-regression analysis]. / N.V. Kuprienko, O. A. Ponomareva, D.V. Tikhonov // St. Petersburg: Publishing House of Polytechnic. un-ta, – 2008. – 118 p. [in Russian]