МЕТОДЫ МОДЕЛИРОВАНИЯ СИСТЕМ АДАПТАЦИИ НАСЕЛЕНИЯ
МЕТОДЫ МОДЕЛИРОВАНИЯ СИСТЕМ АДАПТАЦИИ НАСЕЛЕНИЯ
Научная статья
ORCID: 0000-0001-5433-8400,
Уральский государственный горный университет, Екатеринбург, Россия
* Корреспондирующий автор (eishangina[at]yandex.ru)
АннотацияТрадиционно модели адаптации населения представляют собой достаточно широкую область исследований, связанную с анализом и описанием социальных, экономических, политических, климатических и других происходящих в обществе процессов. В статье с позиции системного подхода рассматриваются вопросы методов моделирования систем адаптации населения. Данная тема актуальна, поскольку классификация объектов по характерным признакам и их анализ является, прежде всего, в том, чтобы получить средство для познания и прогнозирования развития сложных объектов. Автор демонстрирует некоторые эвристические возможности использования концептуальных фрактальных моделей в социально-экономическом знании. Целью данной статьи является прикладное представление в аспекте адаптации населения принципов нелинейной динамики (синергетики) – современным методом познания динамических процессов, возникшим в результате неустойчивости социальных, экономических, политических и др. процессов современной жизни, задачей – систематизация данных о научном потенциале фрактальной теории, а также механизм адаптационных процессов для подтверждения возможности ее использования как концептуальной составляющей современной синергетики.
Ключевые слова: управление изменениями, адаптация населения, модели адаптации населения, нелинейная динамика, синергетика, фрактальность.
MODELING METHODS OF POPULATION ADAPTATION SYSTEMS
Research article
Shangina E.I.*
ORCID: 0000-0001-5433-8400,
Ural State Mining University, Yekaterinburg, Russia
* Corresponding author (eishangina[at]yandex.ru)
AbstractTraditionally, models of population adaptation represent a fairly broad field of research related to the analysis and description of social, economic, political, climatic and other processes that occur in society. The current article examines the issues of methods of modeling the population adaptation systems from the point of view of the system approach. The topic under study can be considered relevant due to the classification of objects by characteristic features as well as their analysis principally serve the purpose of obtaining a means for knowing and predicting the development of complex objects. The author demonstrates certain heuristic possibilities of using conceptual fractal models in socioeconomic knowledge. The purpose of this article is an applied representation of the principles of nonlinear dynamics (synergetics) in the aspect of adaptation of population, a modern method of cognition of dynamic processes that arose as a result of the instability of social, economic, political, and other processes of modern life. The aim of the study is to systematize data on the scientific potential of fractal theory as well as the mechanism of adaptation processes to confirm the possibility of its use as a conceptual component of modern synergetics.
Keywords: change management, population adaptation, model of population adaptation, nonlinear dynamics, synergetics, fractality.
По использованию методов моделирования широкое распространение получили методы математического моделирования. Математические модели делятся на две большие группы: аналитические и алгоритмические (которые иногда называют имитационными). Применение методов математического моделирования дает возможность разработать математические модели социальных процессов адаптации населения в целом и локальных сообществ, в частности, их стратегии адаптации к глобальному изменению климата на планете, к стихийным бедствиям и их последствиям, оценить влияние генерации, накопления, интеграции и использования знаний, а также влияние различных социальных, экономических, политических и иных изменений. Имитационное моделирование – наиболее мощный и универсальный метод исследования и оценки эффективности систем, поведение которых зависит от воздействия случайных факторов. Имитационное моделирование базируется на использовании динамических математических моделей экономических объектов в режиме имитации. В основе имитационного моделирования лежит статистический эксперимент (метод Монте-Карло), реализация которого практически невозможна без применения средств вычислительной техники. Поэтому любая имитационная модель представляет собой в конечном счете более или менее сложный программный продукт. В условиях современных информационных технологий под имитацией принято понимать изучение объектов путем проведения экспериментов с программной реализацией [1]. Главная особенность имитационного исследования заключается в том, что в нем проводятся эксперименты не с реальным объектом / процессом, а с его математической моделью.
В последнее время для исследования систем особую роль играют методы нелинейной динамики (синергетика, теория динамического хаоса), которые непосредственно связаны с фрактальной теорией моделирования систем. Одной из причин создания синергетики стала неустойчивость социально-экономической ситуации в мире и являлась одним из методов познания неустойчивых систем. Наблюдаемое свойство фрактальности в исследуемых синергетикой структурах различных систем, в частности, социальных, экономических, политических и др., получило особое развитие на современном этапе синергетического знания. Фрактальная методология позволяет создавать математические модели социально-экономических процессов. Б. Мандельброт, определяя фрактал как «структуру, состоящую из частей, которые в каком-то смысле подобны целому», выделял два основных признака фрактала: изломанность и самоподобие [2]. Свойство изломанности учитывается в статистических методах оценки систем, а именно, при расчете дробной (фрактальной) размерности, получаемых графических характеристик процессов. Свойство самоподобия представляет научный феномен, когда небольшая часть фрактала содержит информацию обо всем фрактале Фрактальные структуры – это способ организованного взаимодействия пространств различной размерности и природы. Тем не менее, теория самоорганизации как наиболее точно описывающая естественные, природные системы имеет огромный потенциал для изучения усложнившихся процессов, происходящих в современном мире, в частности, их прогнозирования.
Применение методов фрактальной геометрии в сфере социальных, экономических, политических и иных изменений оказалось эффективным, реализация их использования в изучении закономерностей социально-экономических систем отображается в работах таких исследователей, как, Курдюмов С.П., Князева Е.Н. [3], Тарасенко В.В. [4], Хайтун С.Д [5] и др. Фрактальный характер некоторых объектов в прикладной синергетике является неоспоримым, что доказано в исследования Б. Мандельброта [2], Г. Айленбергера [6], В.Т. Гринченко [7], Кузнецов Б.Л. [8] и т.д. Однако, понятие фрактальности не получило единого однозначного мнения по поводу возможности его использования в отношении процессов адаптации населения. Поэтому целью данной статьи является рассмотрение принципов нелинейной динамики (синергетики) – современным методом познания динамических процессов, возникшим в результате неустойчивости социальных, экономических, политических и др. процессов современной жизни. Поэтому представляется актуальной задача как систематизации данных о научном потенциале этого понятия, так и подтверждения возможности его использования как концептуальной составляющей современной синергетики. Синергетика изучает процессы самоорганизации сложных систем различной природы, причем, в некоторых процессах возникает синергетический эффект, когда согласованное взаимодействие подсистем различной природы приводят появлению нового качества, абсолютно иного порядка. Другими словами, система самоорганизуется, т.е. из хаоса возникает упорядоченная структура (фрактал). Фрактал (от лат. fractus – дробный, сломанный) – это геометрическая фигура, в которой один и тот же фрагмент повторяется при каждом уменьшении масштаба (по определению Лаверье).
Адаптация населения как система рассматривается нами как интеграция двусторонних процессов взаимодействия двух подсистем: социальных субъектов с социальной (экономической, политической и др.) средой, в ходе которого меняется не только субъект, но и среда. Она предстает одновременно как эволюционный процесс и как конкретное состояние, свойство и результат освоения меняющихся условий жизнедеятельности. Поэтому адаптацию населения можно рассматривать как сложную систему.
Фрактальная структура системы, т.е. определенная упорядоченность (снижение уровня хаоса) позволяет управлять этими системами при малом воздействии (флуктуации). Однако это возможно, когда система обладает следующими взаимосвязанными синергетическими принципами [9].
- Принцип баланса хаоса и порядка. Эволюционный процесс реализуется сменой условных состояний порядка и хаоса в структуре системы. Конвертация структур системы из порядка в хаос базируется на теории фазовых переходов. Природа хаоса представляет возможность управлять им, т.е. небольшое воздействие (флуктуация) на неустойчивую систему делает их чрезвычайно чувствительными к управлению.
Для понимания этого принципа предположим, что пусть требуется перевести рассматриваемую нами систему (переместить траекторию развития системы) из одной точки фазового пространства в другую. Ярким примером может служить пандемия, вызванная появлением нового вируса Covid-19, что привело к новым условиям жизнедеятельности в изменившихся реалиях и адаптации населения (к примеру, в области образования –переход на информационные технологии). Такое явление одномоментного перехода из одного фазового состояние в другое называется точкой бифуркации (от лат. bifurcus – «раздвоенный»; от лат. be – «два», furcatus – «разделенный» – точка в развитии чего-то, предполагающая вариативность развития), отметим, что бывают случаи полифуркации (например, при разрушении системы). Бифуркация, обусловлена новым элементом в системе или воздействием на управляющий параметр, запускает динамический процесс, который приводит к дальнейшей самоорганизации системы. По завершении процесса самоорганизации эволюционирующая система переходит в новое относительно устойчивое состояние.
- Принцип незамкнутости (открытости) системы подразумевает, наличие доступа входа и выхода источникам энергии, вещества, информации, обмен знаниями и др. со средой жизнедеятельности (обмен материальными и нематериальными ресурсами). Таким образом, открытые системы, которыми являются системы адаптации населения, демонстрируют одновременно и хорошую управляемость, и удивительную гибкость в реакции на внешние воздействия, при этом накопление и усиление малых флуктуаций приведут к существенной коррекции развития.
- Принцип нелинейности представляет процесс нелинейного взаимодействия системы с окружающей средой, которая является источником для обогащения самой системы (посредством появления новых прикладных задач, новых направлений исследования, новых средств и др.) и, благодаря этому, система формируется для умножения потенциала самой среды. Следовательно, прогресс адаптации населения как системы происходит как под воздействием внутренних потребностей развития, так и под внешним влиянием запросов междисциплинарной среды. Нелинейные явления основываются на нарушении принципа суперпозиции, т.е. целое не есть сумма его частей. Суммарная сила связи между подсистемами больше, чем отдельно взятая подсистема. В нашем случае, если социальные субъекты могут взаимодействовать со средой жизнедеятельности, то они могут выйти на новый, более качественный уровень, т.е. обе подсистемы могут взаимодействовать (все связанные друг с другом подсистемы движутся хотя и хаотически, но одинаково, синхронно). Например, развитие всемирной коммуникации, прежде всего, это интернет позволяет экспоненциально увеличить зону адаптации населения в различных сферах жизнедеятельности. В самом общем виде нелинейность может трактоваться как многовариантность и непредсказуемость перехода системы из одного состояния в другое. Принцип нелинейности перетекает в принцип когерентности. Принцип когерентности (принцип эффективности взаимодействия). Когерентность – это проявление системных свойств сложных систем, когда импульсы сложных составных частей сложной системы совпадают по вектору и частоте, то есть осуществляется синхронизация. [10]. От эффективности взаимодействия элементов внутри системы подсистем, а также их взаимодействие внешней средой зависит развитие системы в целом.
- Принцип неустойчивости трактуется как одно из условий и предпосылок стабильного и динамического развития системы, обеспечивая его обновление за счет чувствительности к внешним воздействиям исследуемой среды, которая поддерживается потоком информации извне, обусловливая получение новых материальных или нематериальных потоков в результате синтеза с этой средой в единое целостное интегрированное знание. Неустойчивость траекторий хаотических систем делает их чрезвычайно чувствительными к управлению. Периоды неустойчивости перемежаются с периодами устойчивости, которые обеспечиваются многообразием, избыточностью элементов в системе, что соответствует периодам реорганизации и организации системы адаптации населения.
- Принцип эмерджентности (динамической иерархичности) описывает возникновение целостности системы, т.е. наличие у системы таких свойств, которые не присущи составляющим элементам. Эмерджентность возникает за счет изменений внешних условий (управляющих факторов высших иерархических уровней) воздействующих на более низкие уровни иерархии с их внутренними потребностями, приводящие к изменению к условиям, процессам и средствам адаптации населения.
- Принцип наблюдаемости подчеркивает, что целостное описание системы складывается из компонентов, при этом создается общее пространство научной картины мира. Возникшее пространство ведет к возникновению междисциплинарной интеграции, которая предполагает взаимосогласованное использование представлений, методов и моделей различного профиля. Это позволяет прогнозировать последствия, происходящих в различных сферах человеческой жизнедеятельности.
Рассмотрев принципы синергетики адаптационных процессов можно разрабтать механизм адаптационных процессов, который нами представляется в следующем виде. Процесс развития системы (адаптация населения) неразрывно связан с принципом неустойчивости. Неустойчивость трактуется как одно из условий и предпосылок стабильного и динамического развития - лишь такого рода системы способны к самоорганизации. Периоды неустойчивости перемежаются периодами устойчивости, которые обеспечиваются многообразием, избыточностью элементов системы. За счёт избыточности система обеспечивает себе:
а) адаптивность (плавное эволюционное развитие с предсказуемыми изменениями, которые в итоге подводят систему к некоторому неустойчивому состоянию);
б) нарушение устойчивости развития системы при случайных внешних воздействиях (флуктуациях), которых в природе не избежать. В период неустойчивости (даже замкнутая) система становится открытой, является чувствительным приемником воздействий других уровней бытия (аттракторов), получает информацию, ранее недоступную ей. Эти состояния неустойчивости, выбора пути развития являются точками бифуркаций (например, возникновение вируса). Они непременно возникают в любой ситуации рождения нового качества и характеризуют рубеж между новым и старым;
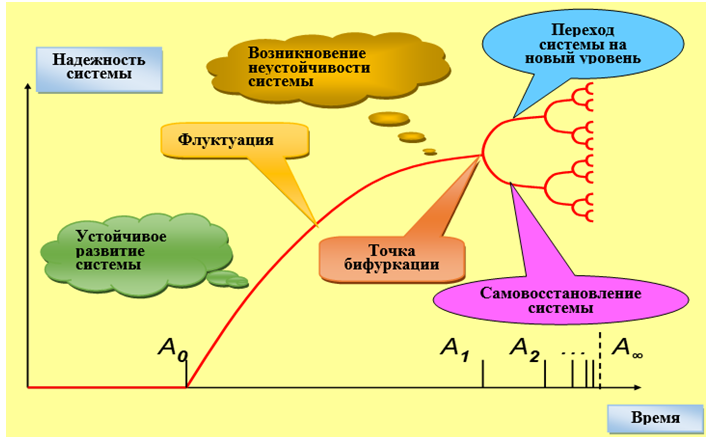
в) одномоментный выход из критического состояния скачком и переход в новое устойчивое состояние. Устойчивость и неустойчивость диалектичны: из неустойчивости вырастает устойчивость, а устойчивость рано или поздно оборачивается неустойчивостью. Устойчивый и неустойчивый этапы, сменяя друг друга, определяют источник развития системы (рис. 1).
Рис. 1 – Схема механизма развития (адаптационных процессов) системы
Заключение
Системно-синергетический взгляд на моделирование систем адаптации населения возникает как некий промежуточный феномен между хаосом и порядком. Данный подход позволяет прогнозировать ситуацию, происходящую в конкретно исследуемой системе. Из хаоса, который изначально преобладает в системе за счет небольших воздействий, пройдя точку бифуркации, могут возникнуть новые качественные структуры, генерируя эффект развития. Такие процессы называют «эффектом бабочки». При этом возникает порядок- фрактальная структура. Фрактальность как концептуальное свойство, наблюдаемое в исследуемых синергетикой структурах, получило особое развитие на современном этапе синергетического знания, преимущественно ориентированного в сферу гуманитарного бытия. В этой связи необходимо еще раз подчеркнуть, что фрактальное моделирование позволяет увидеть системность там, где ее на первый взгляд ее нет. И здесь особую роль играет феномен масштабирования, который предполагает четкую локализацию объекта и субъекта исследования. От этой локализации зависит детальность изучения объектов исследования.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Шмаков В. С. К проблеме моделирования социальных процессов / В. С. Шмаков, Ю. С. Сердюкова // Гуманитарные науки в Сибири. 2009. № 1. С. 46–49.
- Mandelbrot B. B. The fractal geometry of nature / B. B. Mandelbrot. N. Y., 1983. 462 c.
- Князева Е.Н. Основания синергетики / Е.Н. Князева, С.П. Курдюмов. СПб., 2002. 414 с.
- Тарасенко В.В. Фракталы и аттракторы социальной эволюции / В.В. Тарасенко. [Электронный ресурс] URL: https://mitchep.livejournal.com/15446.html (дата обращения: 24.12.2020).
- Хайтун С.Д. От эргодической гипотезы к фрактальной картине мира / С.Д. Хайтун. М., 2007. 256 с.
- Айленбергер Г. Свобода, наука и эстетика / Г. Айленбергер // Рихтер Х.-О. Красота фракталов. Образы комплексных динамических систем. М., 1993. С. 176.
- Гринченко В.Т. Введение в нелинейную динамику. Хаос и фракталы / В.Т. Гринченко, В.Т. Мацыпура, А.А. Снарский. М., 2007. 264 с.
- Кузнецов Б.Л. Введение в экономическую синергетику / Б.Л. Кузнецов. Набережные Челны: Изд-во КамПИ, 1996-1999. 398 с.
- Шангина Е. И. Методологические основы формирования структуры и содержания геометро-графического образования в техническом вузе в условиях интеграции с общеинженерными и специальными дисциплинами / Е. И. Шангина: дис. … д-ра пед. наук. М., 2010. – 365 с.
Список литературы на английском языке / References in English
- Shmakov V. S. probleme modelirovanija social'nykh processov [On the Problem of Modeling of Social Processes]/ V. S. Shmakov, Yu. S. Serdyukova// Gumanitarnye nauki v Sibiri [Humanities in Siberia]. 2009. № 1, pp. 46-49 [in Russian]
- Mandelbrot B. B. The fractal geometry of nature / B. B. Mandelbrot. N. Y., 1983. 462 p.
- Knyazeva E. N., Kurdyumov S. P. Osnovanija sinergetiki [Fundamentals of Synergetics]/ E. N. Knyazeva, S. P. Kurdyumov. St. Petersburg, 2002. 414 p. [in Russian]
- Tarasenko V. V. Fraktaly i attraktory social'nojj ehvoljucii [Fractals and Attractors of Social Evolution] / V. V. Tarasenko. [Electronic resource] URL: https://mitchep.livejournal.com/15446.html (accessed: 24.12.2020) [in Russian]
- Haitun S. D. Ot ehrgodicheskojj gipotezy k fraktal'nojj kartine mira [From the ergodic hypothesis to the fractal picture of the world] / S. D. Haitun. Moscow, 2007. 256 p. [in Russian]
- Eilenberger G. Svoboda, nauka i estetika [Freedom, Science, and Aesthetics]. H. Richter [The Beauty of Fractals. Images of Complex Dynamic Systems]. M., 1993, p. 176. [in Russian]
- Grinchenko V. T. Vvedenie v nelinejjnuju dinamiku. Khaos i fraktaly [Introduction to Nonlinear Dynamics. Chaos and Fractals]. Moscow, 2007, 264 p. [in Russian]
- Kuznetsov, B. L. Vvedenie v ehkonomicheskuju sinergetiku [Introduction to Economic synergy]/ B. L. Kuznetsov. Naberezhnye Chelny: Publishing house KamPI, 1996-1999, 398 p. [in Russian]
- Shangina, E. I. Metodologicheskie osnovy formirovanija struktury i soderzhanija geometro-graficheskogo obrazovanija v tekhnicheskom vuze v uslovijakh integracii s obshheinzhenernymi i special'nymi disciplinami [Methodological Foundations of the Formation of the Structure and Content of Geometric and Graphic Education in a Technical University in the Context of Integration With General Engineering and Special Disciplines]: Doctor's Thesis/ E. I. Shangina. Moscow, 2010. - 365 p. [in Russian]