ВЛИЯНИЕ ЭЛЕКТРИЧЕСКОГО ПОЛЯ НА РИДБЕРГОВСКИЕ nD-СОСТОЯНИЯ ХОЛОДНЫХ АТОМОВ ЛИТИЯ

ВЛИЯНИЕ ЭЛЕКТРИЧЕСКОГО ПОЛЯ НА РИДБЕРГОВСКИЕ nD-СОСТОЯНИЯ ХОЛОДНЫХ АТОМОВ ЛИТИЯ

Научная статья

Бронин С.Я.¹, Бобров А.А.^2, *, Фомичев Д.Е.³, Саакян С.А.⁴, Саутенков В.А.⁵, Зеленер Б.Б.⁶, Зеленер Б.В.⁷

^{1, 2, 3, 4, 5, 6, 7} Объединенный институт высоких температур Сибирского отделения Российской академии наук, Москва, Россия;

⁵ Физический институт им. Н. П. Лебедева Сибирского отделения Российской академии наук, Москва, Россия;

⁶ Национальный исследовательский университет — Московский энергетический институт, Москва, Россия;

⁶ Национальный исследовательский университет — Московский инженерно-физический институт, Москва, Россия

* Корреспондирующий автор (abobrov[at]inbox.ru)

Аннотация

В работе исследуется влияние слабого электрического поля на когерентный двухфотонный резонанс 2S-nD методом регистрации падения флюоресценции атомов Li в магнитооптической ловушке. В экспериментах наблюдалось, что под действием слабого нескомпенсированного электрического поля отдельная линия за счет эффекта Штарка превращается в полосу. При этом ширина полосы растет с ростом значения главного квантового числа n (или величины электрического поля). Показано, что резонансное излучение, настроенное на левый или правый край полосы, позволяет получить газ ридберговских атомов с постоянным большим дипольным моментом , ориентированным соответственно вдоль или против поля. Излучение, настроенное в центр полосы позволит получить атомные состояния с нулевым дипольным моментом, но с большим вкладом состояний с максимальным значением орбитального квантового числа .

Ключевые слова: эффект Штарка, ридберговские атомы.

INFLUENCE OF ELECTRIC FIELD ON RYDBERG ND-STATES OF COLD LITHIUM ATOMS

Research article

Bronin S.Ya.¹, Bobrov A.A.^2, *, Fomichev D.E.³, Saakyan S.A.⁴, Sautenkov V.A.⁵, Zelener B.B.⁶, Zelener B.B.⁷

^{1, 2, 3, 4, 5, 6, 7} Joint Institute for High Temperatures RAS, Moscow, Russia;

⁵ P.N. Lebedev Physical Institute of the Russian Academy of Sciences, Moscow, Russia;

⁶ National Research University – Moscow Power Engineering Institute, Moscow, Russia;

⁶ National Research University – Moscow Engineering Physics Institute, Moscow, Russia

* Corresponding author (abobrov[at]inbox.ru)

Abstract

The effect of the weak electric field on the coherent two-photon resonance 2S-nD is considered in the work by means of recording the fluorescence incidence of Li atoms in the magneto-optical trap. In the course of experiments, it was observed that a separate line is transformed into a band due to the Stark effect under the effect of the weak uncompensated electric field. In this case, the width of the band increases with the increase of the value of the principal quantum n number (or the value of the electric field). It is shown that resonant radiation tuned to the left or right edge of the line allows obtaining gas of Rydberg atoms with a constant large dipole moment  oriented along or against the field, respectively. The radiation tuned to the center of the band will allow obtaining atomic states with a zero dipole moment but with a large contribution of states with a maximum value of the orbital quantum number .

Keywords: Stark effect, Rydberg atoms.

Введение

Ридберговские атомы очень чувствительны к внешним электрическим и магнитным полям. В большинстве экспериментов существенный вклад в ширину наблюдаемых ридберговских переходов дают нескомпенсированные паразитные электрические поля. Чувствительность ридберговских атомов к полю растет очень быстро с ростом главного квантового числа как n⁷.

В работе [1] поле было уменьшено до 45 мкВ/см, что позволило наблюдать ридберговские состояния бария с n=520. В работе [2] ридберговские состояния использовались для измерения слабых электрических полей и была достигнута точность порядка 20 мкВ/см. В реальных экспериментальных условиях полностью компенсировать электрические поля практически невозможно. Измерительная аппаратура и системы регистрации заряженных частиц являются потенциальными источниками электрического поля. Исследуемые атомы могут осаждаться в виде пленок на элементах системы регистрации и создавать контактную разность потенциалов [3]. При этом остаточное электрическое поле может приводить к возбуждению ридберговских состояний, с большим орбитальным квантовым числом l. Состояния с большим l (водородоподобные состояния) [4] имеют большой дипольный момент.

В данной работе экспериментально, по падению резонансной флуоресценции нейтральных атомов лития-7 в магнито-оптической ловушке (МОЛ) [5], [6], изучалось влияние не скомпенсированного электрического поля на ширину ридберговских резонансов 49D, 59D, 70D, и 82D. Были сделаны квантово-механические расчеты для исследуемых ридберговских состояний с учетом эффекта Штарка в рамках теории возмущений. Получено хорошее согласие с экспериментальными результатами для всех рассматриваемых ридберговских состояний при подстановке в уравнения значения поля E=12 мВ/см. Близкое значение поля было получено нами ранее другим способом [7]. Показано также, что при наличии даже слабого электрического поля резонансное излучение, настроенное на левый или правый край полосы, позволяет получить газ ридберговских атомов с постоянным большим дипольным моментом ориентированным соответственно вдоль или против поля.

Эксперимент

Все описанные в данной работе эксперименты проводились в МОЛ для атомов лития, подробное описание которой можно найти в работах [5], [6], [7].

Для лазерного охлаждения и захвата в МОЛ атомов лития используется два лазера с длиной волны 671 нм. Первый охлаждающий лазер  стабилизирован на частоте перехода . Второй охлаждающий лазер  стабилизирован на частоте перехода . В каждом из шести пучков, формирующих МОЛ, соблюдается отношение интенсивностей . Суммарная интенсивность пучков МОЛ = 72 мВт/см².

Двухфотонные резонансы в ридберговские состояния возбуждаются двумя встречными лазерными пучками  (Рис. 1(б)) для уменьшения доплеровского уширения. Лазерный пучок  формируется охлаждающим лазером стабилизированным на переходе  и отстроен от перехода на частоту МГц в красную сторону. Пучок  является результатом удвоение частоты титан-сапфирового лазера, который стабилизировался на высокодобротном интерферометре Фабри-Перо методом PDH [8]. Интенсивность УФ-пучка  во всех экспериментах не превышала 3 мВт/см². Резонансы в ридберговские состояния регистрировались по падению резонансной флуоресценции нейтральных атомов лития в МОЛ [6].

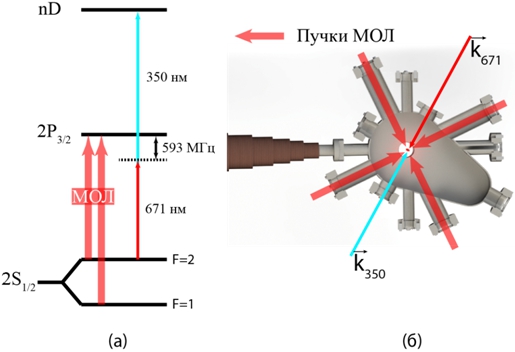
Рис. 1 – Диаграмма уровней ⁷Li (а) и принципиальная схема эксперимента (б)

 

Форма резонансных спектральных линий для всех  определяется совместным действием неоднородного доплеровского (гауссова) и однородного (лоренцева) уширения, обусловленного в основном уширением полем пучков МОЛ. Во всех экспериментах температура атомов была порядка 0.6 мК, при этой температуре доплеровская полуширина составляет 1,8 МГц. Суммарная интенсивность пучков МОЛ 72 мВт/см², что соответствует лоренцевой полуширине порядка 2,8 МГц. Подробное исследование влияния интенсивности пучков МОЛ на ширину двухфотонных ридберговских резонансов можно найти в работе [9]. Суммарная полуширина линий красного и УФ-лазера (на рис. 1(б)  и  соответственно) составляла порядка 0.2 МГц [10].

На рис. 2 показан спектральный профиль когерентного двухфотонного резонанса . Здесь сдвиг и расщепление перехода  за счет действия электрического поля незначительны по сравнению с шириной наблюдаемого резонанса. Расчетный резонанс представлен в виде свертки функций Лоренца и Гаусса (профиль Фойгта), отношение полевого

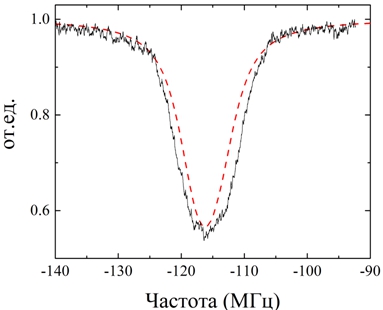
Рис. 2 – Форма линии двухфотонного когерентного перехода : Черная сплошная линия – экспериментальные данные; красная пунктирная линия представляет результат расчетов уширения к допплеровскому составляет 1.5.

 

Ширина наблюдаемых резонансов увеличивалась с ростом значения главного квантового числа n. Для описания этого уширения необходимо учитывать расщепление состояний nD за счет эффекта Штарка. В части 3 настоящей работы рассмотрен эффект Штарка и в части 4 производится сравнение полученных экспериментальных данных с расчетами.

Теоретическая модель штарковского расщепления

В отсутствие электрического поля спектр поглощения в интервале между двумя соседними водородными уровнями представлен двумя спектральными линиями . С появлением электрического поля в процесс поглощения, благодаря эффекту Штарка, начинают вовлекаться  уровня со значениями орбитального числа  и магнитными квантовыми числами . Связано это с тем, что в разложении каждого штарковского состояния по невозмущенным собственным состояниям присутствует компонента nD, благодаря чему каждое такое состояние связано с уровнем  дипольным матричным элементом, делающим возможным резонансный переход в это состояние. В результате с ростом напряженности поля одиночная спектральная линия превращается в полосу, состоящую из  линий. Формирующие эти полосы уровни попарно связаны друг с другом матричными элементами

где радиус атома   рассчитывается с использованием квазиклассического приближения, ,  – множитель разложения сферической функции . Дефект уровня nD  равен , дефектами остальных уровней можно пренебречь так, что в невозмущенной системе уровни энергии представлены двумя значениями: и энергией n-го водородного уровня расстояние между которыми равно .

При не слишком больших значениях поля E, когда влиянием уровня nP можно пренебречь, возмущенные уровни энергии и соответствующие им состояния являются собственными значениями и собственными функциями матричного оператора  с размерностью . Около диагональные элементы матрицы  равны: . При малых значениях E поля  имеет место квадратичный Штарк-эффект, при больших – линейный. Граничным значением поля E_st является его величина, при которой .

Собственные значения энергии  определяются численным решением уравнения. По известным значениям  коэффициенты разложения собственных функций по функциям невозмущенной системы  определяются из системы уравнений:

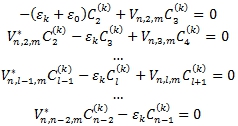   (1)

Ширина полосы  также, как и для водорода дается равенством . Поскольку в каждом из  n-2 собственных состояний присутствует состояние  с некоторым коэффициентом , то каждое из них связано с состоянием  с силой осциллятора пропорциональной , причем . По этой причине отдельная линия с фиксированным значением магнитного числа при включении поля превращается в полосу, состоящую из n-2 линий с той же суммарной силой осциллятора и шириной пропорциональной величине электрического поля при .

Собственные состояния , в отличие от состояний , имеют отличные от 0 средние значения , проекции дипольного момента на направление поля:

где .

Умножая каждое уравнение (1) на  и суммируя, получим:

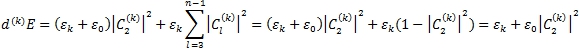   (2)

При малых  правая часть (2) пропорциональна квадрату E и , при больших  она пропорциональна E и среднее значение дипольного момента не зависит от E. Сумма по k всех значений  всегда равна 0, в чем можно убедиться просуммировав (2):

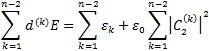   (3)

Первая сумма в правой части (3) равна шпуру оператора , вторая сумма равна единице, поскольку величины  являются  коэффициентами разложения состояний  по ортонормированной системе функций . Окончательно имеем .

 

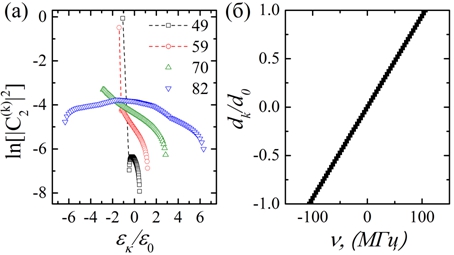
Рис. 3 – (а) Значения  в разложении k-й штарковской компоненты по сферическим функциям в зависимости от энергии штарковского уровня  (энергия отсчитывается от n-го водородного уровня,  – энергия уровня мВ/см. (б) Дипольный момент ридберговских атомов, нормированный на его максимальное значение  как функция частоты резонансного поглощения,  мВ/см

На рис. 3 (a) представлены величины  в зависимости от энергии штарковских уровней, отсчитываемой от n-го водородного уровня, для n= 49, 59, 70, 82, m=0 и . Значения отношения  равны соответственно: 0.49, 1.24, 2.92 и 6.45. При n= 49 и 59 с малыми значениями отношения , доминируют коэффициенты , представляющие слабо смещенные состояния  (квадратичный штарк-эффект). При n= 70 и 82 все n - 2 штарковских уровня участвуют в формировании полосы, которая с ростом n становится все более симметричной относительно водородного уровня (линейный штарк-эффект), приближаясь в пределе к результату, реализующемуся для атома водорода. Поскольку  такая же эволюция имеет место при увеличении Е при фиксированном n. На рис. 3 (б) представлены значения дипольных моментов штарковских уровней в зависимости от их энергии, отсчитываемой от водородного уровня, для . Практически идеальная пропорциональная зависимость этих величин, означает линейность штарк-эффекта при котором значения дипольных моментов перестают зависеть от величины поля.

Таким образом, при наличии даже слабого электрического поля резонансное излучение, настроенное на край штарковской полосы, позволяет получить газ ридберговских атомов с большим дипольным моментом , ориентированным либо вдоль поля (правый край полосы ), либо против поля (левый край ).

Коэффициент поглощения полосы  является суммой вкладов всех собственных состояний возмущенной системы и дается равенством:

   (4)

где  – общая для всех штарковских состояний форма спектральной линии,  – энергетические уровни для данных значений m и n, выраженные в единицах частоты и .

Условиям эксперимента, как следует из расчетов, выполненных в [9], соответствует фойгтовский профиль спектральной линии  с отношением лоренцевой полуширины к доплеровской равным 1,51. Расчетные значения представлены в виде , где λ – подгоночный параметр, характеризующий оптическую глубину облака атомов.

На рис. 4 представлены функции . Уравнение (4) определяет статвес, для невозмущенных функций с данным значением орбитального углового момента l. Вследствие уширения линий, описываемых фойгтовским профилем , в возбужденном состоянии смешано несколько соседних штарковских уровней. Как видно на рис. 4, состояния с максимальным орбитальным моментом дают основной вклад в штарковсие состояния вблизи энергии, соответствующей водородному уровню (т. е. когда квантовый дефект равен нулю).

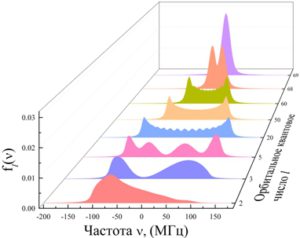
Рис. 4 – Вес, с которым невозмущенные функции с данным орбитальным угловым моментом l входят в разложение состояния, которое возникает при резонансном поглощении излучения на данной частоте для n=70,

 

Результаты и обсуждение

На рис. 2 представлен резонанс в состояние 49D. Здесь влияние электрического поля сводится к небольшому смещению линии  и незначительному ее расщеплению на три компоненты, соответствующие зеемановским подуровням, малому по сравнению с шириной самой линии.

На рис. 5(а)-(в) представлены когерентные двухфотонные резонансы в 59, 70 и 82 состояние. Наблюдаемая ширина резонансов хорошо согласуется с теоретической моделью. При n=59 расщепление по зеемановским подуровням становится заметным: сдвиг подуровней, соответствующих  превышает ширину линий. Кроме того, становится заметным вклад остальных штарковских уровней, формирующих полосу справа от основной линии. При n=70 и 82 одиночные спектральные линии заменяются спектральными полосами, в которых участвуют все штарковские уровни, в том числе уровни с энергиями большими n-го водородного уровня.

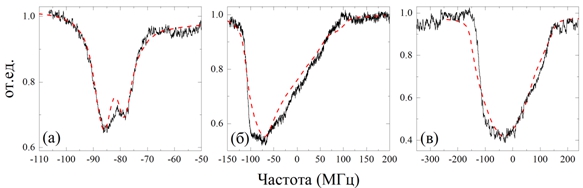
Рис. 5 – Двухфотонные когерентные резонансы в ридберговские состояния (а) 59D, (б) 70D, (в) 82D; черная кривая – эксперимент, красная пунктирная – теоретическая кривая при остаточном поле в вакуумной камере 12 мВ/см; ноль по оси абсцисс соответствует частоте водородного уровня с соответствующим главным квантовым числом

 

Результаты расчетов, представленные на рис. 4 также как экспериментальные и теоретические кривые на рис. 5(в) демонстрируют возможность перевода атомов в состояния с произвольным орбитальным угловым моментом для любого значения главного квантового числа с вероятностью возбуждения, пропорциональной энергии возбуждения.

Ридберговские атомы с максимальными значениями орбитального углового момента могут быть возбуждены с вероятностью 14% в присутствии небольшого поля, когда частота поля лазера настроена на уровень с нулевым квантовым дефектом.

Анализ полученных экспериментальных результатов показал, что при наличии даже слабого электрического поля отдельная линия ридберговского уровня энергии превращается в полосу и резонансное излучение, настроенное на левый или правый край полосы, позволяет получить газ ридберговских атомов с постоянным большим дипольным моментом. В условиях эксперимента температура этого газа ~ 10^-3 K, а плотность может достигать 10⁹ см^-3.

В работах [13], [14], [15], [16], [17] были предложены и апробированы методики пространственной визуализации ридберговских атомов. Причем в [13], по всей видимости, наблюдалась цепочка атомов. Использование этих методик позволит изучить свойства плотной фазы резонансно возбужденного газа. Изучение самоорганизации и анизотропии свойств газа ридберговских атомов за счет наличия выделенного направления электрического поля открывает новые направления в физике ультрахолодных газов, а также дает возможность учесть эти эффекты в резонансно возбужденных газах, например, при комнатных температурах.

Заключение

В представленной работе было исследовано влияние слабого электрического поля на когерентное возбуждение ридберговских состояний на переходе  с использованием метода регистрации резонансной флюоресценции атомов лития в МОЛ. Наблюдался переход узкой линии в полосу вследствие эффекта Штарка. Спектральная ширина полосы увеличивалась с увеличением значения главного квантового числа n. Для описания наблюдаемой спектральной формы полосы были сделаны расчеты в рамках теории возмущений. Результаты расчетов показали, что линейный эффект Штарка может привести к образованию ридберговских атомов с постоянными дипольными моментами. Экспериментально наблюдаемые спектры ридберговских состояний nD хорошо согласуются с результатами расчетов.

Финансирование Работа поддержана Программой фундаментальных исследований Президиума Российской академии Наук «Исследование вещества в экстремальных состояниях» под руководством академика Фортова В.Е.	Funding This work was supported by the Basic Research Program of the Presidium of the Russian Academy of Sciences “Study of Substance in Extreme States” under the supervision of Academician Fortov V.Ye.
Благодарности Авторы признательны сотрудникам Теоретического отдела им. Л. М. Бибермана за полезные и конструктивные замечания.	Acknowledgement The authors are grateful to the staff of the Theoretical Department named after L. M. Biberman for useful and constructive comments.
Конфликт интересов Не указан.	Conflict of Interest None declared.

Список литературы / References

1. Neukammer J. Spectroscopy of Rydberg atoms at n≈500: Observation of quasi-Landau resonances in low magnetic fields / J. Neukammer, H. Rinneberg,K. Vietzke and others// Physical review letters. – 1987. – Vol. 59. – №. 26. – P. 2947.
2. Osterwalder A. Using high Rydberg states as electric field sensors / A. Osterwalder, F. Merkt // Physical review letters. – 1999. – Vol. 82. – №. 9. – P. 1831.
3. Tretyakov D. B. Effect of photoions on the line shape of the Förster resonance lines and microwave transitions in cold rubidium Rydberg atoms / D. Tretyakov, I. I. Beterov, V. M. Entin and others // Journal of Experimental and Theoretical Physics. – 2012. – Vol. 114. – №. 1. – P. 14-24.
4. Zimmerman M. L. Stark structure of the Rydberg states of alkali-metal atoms / M. L. Zimmerman, M. G. Littman, M. Kash and others // Physical Review A. – 1979. – Vol. 20. – №. 6. – P. 2251.
5. Sautenkov V. A. Observation of Rydberg Transitions in Resonance Fluorescence of Ultracold Lithium-7 Atoms / V. A. Sautenkov, S. A. Saakyan, E. V. Vilshanskaya and others // Journal of Russian Laser Research. – 2015. – Vol. 36. – №. 2. – P. 193-199.
6. Zelener B. B. Efficient excitation of Rydberg states in ultracold lithium-7 atoms / B. B. Zelener, S. A. Saakyan, V. A. Sautenkov and others // JETP letters. – 2014. – Vol. 100. – №. 6. – P. 366-370.
7. Zelener B. B. Laser diagnostics of the energy spectrum of Rydberg states of the lithium-7 atom / B. B. Zelener S. A. Saakyan, V. A. Sautenkov and others // Journal of Experimental and Theoretical Physics. – 2015. – Vol. 121. – №. 6. – P. 950-954.
8. Saakyan S. A. Long-term frequency stabilized and linewidth-narrowed cw-laser system for excitation of lithium Rydberg states / S. A. Saakyan, V. A. Sautenkov, B. B. Zelener // Journal of Physics: Conference Series. – IOP Publishing, 2018. – Vol. 946. – №. 1. – P. 012128.
9. Sautenkov V. A. Differential two-photon spectroscopy for nondestructive temperature measurements of cold light atoms in a magneto-optical trap / V. A. Sautenkov, S. A. Saakyan, A. A. Bobrov and others // JOSA B. – 2018. – Vol. 35. – №. 7. – P. 1546-1551.
10. Bobrov A. A. Determination of characteristics of a magneto-optical trap by the spectral width of coherent two-photon resonance / A. A. Bobrov, S. A. Saakyan, V. A. Sautenkov and others // Quantum Electronics. – 2018. – Vol. 48. – №. 5. – P. 438.
11. Lifshitz E. M. Quantum Mechanics Non-relativistics Theory / E. M. Lifshitz, J. Menzies, L. D. Landau. – Elsevier Science, 1996.
12. D'yachkov L. G. The hydrogen Balmer spectrum in the near-threshold region: unified semiclassical calculation of line and continuum contributions / L. G. D'yachkov, G. A. Kobzev, P. M. Pankratov // Journal of Physics B: Atomic, Molecular and Optical Physics. – 1988. – Vol. 21. – №. 10. – P. 1939.
13. Carroll T. J. Many-body interactions in a sample of ultracold Rydberg atoms with varying dimensions and densities / T. J. Carroll, S. Sunder, M. W. Noel // Physical Review A. – 2006. – Vol. 73. – №. 3. – P. 032-725.
14. van Ditzhuijzen C. S. E. Spatially resolved observation of dipole-dipole interaction between rydberg atoms / C. S. E. Van Ditzhuijzen, A. F. Koenderink, J. V. Hernandez and others // Physical Review Letters. – 2008. – Vol. 100. – №. 24. – P. 243-201.
15. Thaicharoen N. Control of spatial correlations between Rydberg excitations using rotary echo / N. Thaicharoen, A. Schwarzkopf, G. Raithel // Physical review letters. – 2017. – Vol. 118. – №. 13. – P. 133-401.
16. Goncalves L. F. Motion of Rydberg atoms with strongpermanent-electric-dipole interactions / L. F. Goncalves N .Thaicharoen N., Raithel G. J. // Journal of Physics B. – 2016. – Т.49. – С. 154005.
17. Schwarzkopf A. Spatial correlations between Rydberg atoms in an optical dipole trap / A. Schwarzkopf, D. A. Anderson, N. Thaicharoen and others //Physical Review A. – 2013. – Vol. 88. – №. 6. – P. 061406.