УРАВНЕНИЯ НАВЬЕ – СТОКСА. ОТ ТЕОРИИ К РЕШЕНИЮ ПРАКТИЧЕСКИХ ЗАДАЧ
Коптев А. В.
Кандидат физико-математических наук, доцент, Государственный университет морского и речного флота имени адмирала С. О. Макарова
УРАВНЕНИЯ НАВЬЕ – СТОКСА. ОТ ТЕОРИИ К РЕШЕНИЮ ПРАКТИЧЕСКИХ ЗАДАЧ
Аннотация
В работе предложен подход к решению практических задач гидромеханики на основе уравнений Навье – Стокса для вязкой несжимаемой жидкости. В результате применения метода решение основных уравнений сводится к решению пяти более простых задач. Каждая из этих отдельных задач решается с помощью известных методов математической физики и дифференциальных уравнений. В итоге применение предлагаемого метода предоставляет возможность для аналитического и приближенно-аналитического решения 2D и 3D уравнений Навье – Стокса и построения решений конкретных практических задач.
Ключевые слова: движение, вязкая несжимаемая жидкость, уравнение в частных производных, интеграл.
Koptev A. V.
PhD in Physics and Mathematics, Admiral Makarov State University of Maritime and Inland Shipping
THE NAVIER – STOKES EQUATIONS. FROM THEORY FORWARD TO SOLUTION OF PRACTICAL PROBLEMS
Abstract
On the paper under consideration we propose an approach to the solution of practical problems of fluid mechanics based on the Navier – Stokes equations for viscous incompressible fluid flow. As a result, the solution of the governing equations is reduced to the solution of five simple tasks. Each of these separate tasks is considered using known methods of mathematical physics and differential equations. As a result, the application of the proposed method provides the ability for analytical and approximate analytical solutions 2D and 3D Navier - Stokes equations and constructing solutions for specific practical problems.
Keywords: motion, viscous incompressible fluid, partial differential equation, integral.
The Navier - Stokes equations describe the motion of fluids and gases in the presence of viscosity. These equations are nonlinear and represent not only mathematical interest but also serve as a basis for the solution of many practical problems. They are of particular interest for areas where the viscous friction effects play an important role. These areas include: oil production, shipbuilding, hydrology, meteorology, tribology.
If the potential of external forces then 3D Navier – Stokes equations for viscous incompressible fluid flow on dimensionless variables look as [1].
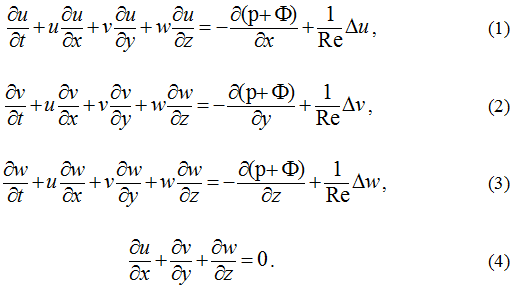
Where major unknowns are velocities u, v, w and pressure p. Each of them is a function of four independent variables x, y, z, t. On right hand sides of (1-3) Δ designated Laplace operator in the spatial coordinates.
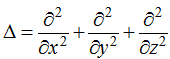
The potential of external force designated as Φ. It is a given function. is the Reynolds number. This value represents a predetermined non-negative parameter.
For today many issues associated with the equations (1-4) have not been studied enough and require more deep investigation [2-3]. No detailed description of the laminar- turbulent transition, not fully solved the problem of existence for smooth solution, not clear asymptotic of the solution for large values of Reynolds number. But the main unresolved problem is the lack of constructive method for solving the equations. As in the general case to solve equations (1-4) while maintaining the non-linear terms, this issue needs to be resolved.
In this paper we proposed to describe a new method for practical solution to the Navier – Stokes equations (1-4). The essence of the proposed approach is to reduce the basic problem of resolution of (1-4) to a set of simple tasks. We face five more simple tasks which should be consistently resolved.
- Each of the separate equations (1-4) can be represented in the divergent form as
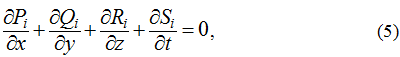
where Pi, Qi, Ri, Si denotes some combinations of major unknowns u, v, w, p and their first derivatives with respect to coordinates. Every equation of the form (5) allows integration in general
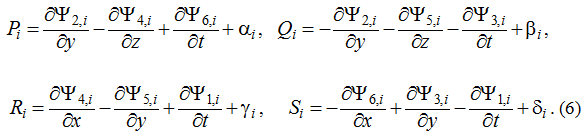
Where , k=1,2,…,6 are some twice differentiable functions in four variables and ![]() are an arbitrary functions in three variables under conditions
are an arbitrary functions in three variables under conditions
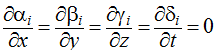
While 3D Navier – Stokes equations including the continuity one combine four ratios as (5), so we obtain relations as (6) for everyone of i=1,2,3,4. In sum, we get sixteen relations of the specified kind.
- Equality of the form (6) can be converted so as to exclude any nonlinear and non-divergent terms. As the result we arrive to nine equations linked major unknowns u, v, w, p, associated ones Ψi , i=1,2, …, 15 and an arbitrary additive functions in three variables
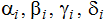 . These equations look as
. These equations look as
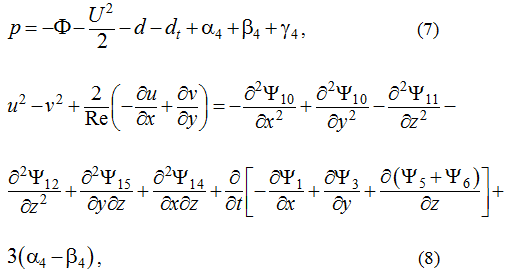
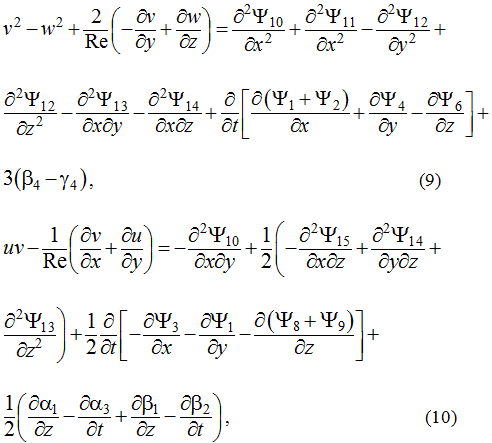
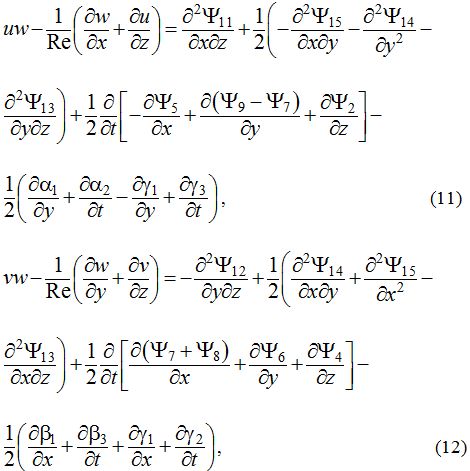
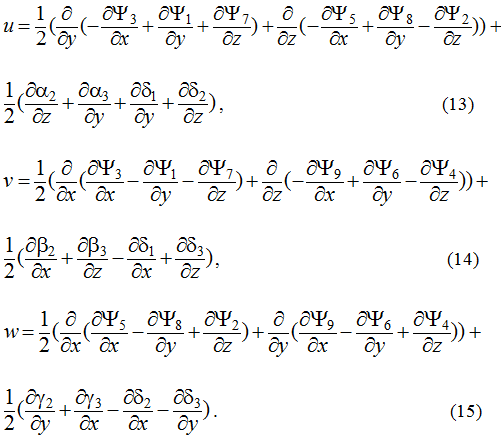
In equation (7) used the new designation. U is the velocity module, d and are dissipative terms calculated as
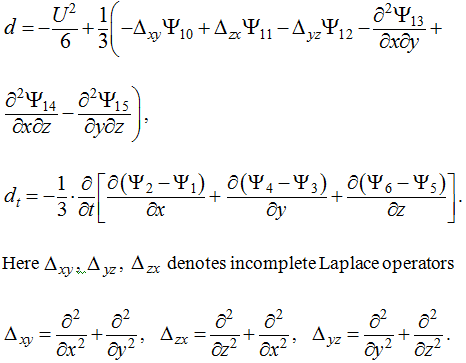
For associated unknown in compared to (6) we introduce more simple designation and propose the name as stream pseudo function [4-5]. Considered together nine ratio (7-15) provide the first integral of Navier – Stokes equations.
- Of the nine received there five nonlinear relationships (8-12). They contain quadratic nonlinear terms. These nonlinear equations can be resolved relative to six unknown Ψj, where j=10,11,…, 15 only if satisfied the two conditions of compatibility. Each of them reduce to one equation of the fifth order with respect to nine unknown Ψk, where k=1,2,…, 9. These two equations can be called the generator of solutions of 3D Navier – Stokes equations. For more simple case of 2D motion such generating equation is only one [5]. All solutions obtained by this way have a similar structure [4]. The structural formulas for solution of original equations (1-4) given by (7), (13-15).
- To complete the solution remains to find unknown p. To do this you must at first determine six unknown Ψj, where j=10,11,…, 15. Three of them can be set arbitrary. Those unknown are the next Ψ13, Ψ14, Ψ15.The remaining three ones are defined as solution of linear inhomogeneous equations
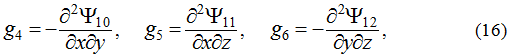
where represent is already known functions.
Equation of the form (14) can be solved by standard methods.
- All values presents in the right hand sides of structure formula (7), (13-15) are defined. Unknown p is easy to calculate. As a result all of the major unknown u, v, w, p are found out. The solution of the Navier – Stokes equations is fully built. Note that similar approach can be applied to construct solutions of the Euler equations which describe an ideal fluid flow. It suffices to set in all relationships
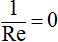 .
.
Fair following conclusions. When implementing this approach is important the introduction of new associated unknowns . Due to this fact the solution of the Navier – Stokes equations for some cases is possible to obtain in closed form.
Among the described above individual tasks most difficult is third one. But at this stage as an enabling factor have a significant excess in the number of unknowns over number of equations. We have nine unknown and only two equations. This fact is convenient for solving practical problems.
The approach described above can be successfully applied to solve a wide range of practical tasks. Solutions of some tasks considered in [5-8].
References
- Loitsyanskiy L. G. Mechanics of fluid and gas // Nauka, Moscow. – 1987.
- Ladyjzenskaya O. A. The mathematical theory of viscous incompressible fluid // Gordon and Breach, New York. – 1969.
- Charles L. Fefferman. Existence and smoothness of the Navier – Stokes equation // Preprint, Princeton university, Math. Dept., Princeton, NJ, USA. – 2000. – P. 1-5.
- Koptev A. V. The structure of solution of the Navier – Stokes equations // Bulletin of the national research nuclear university MEPI. – 2014. – 3(6). – P. 556-560.
- Koptev A. V. Generator of solution of 2D Navier – Stokes equations // Journal of Siberian federal university, Math. & Phys. – 2014. – 7(3). – P. 324-330.
- Koptev A. V. Dynamic response of the underwater pipeline on the sea currents // Vestnik gosudarstvennogo universiteta morskogo i rechnogo flota im. adm. S.O. Makarova. – 2014. – 4(26). – P. 107-114 (in Russian).
- Koptev A.V. Research of influence of underwater current on the dynamics of the ship // Vestnik gosudarstvennogo universiteta morskogo i rechnogo flota im. adm. S.O. Makarova. – 2015. – 2(30). – P. 16-23 (in Russian).
- Koptev A. V. Theoretical research of the flow around the cylinder of an ideal incompressible medium in the presence of a shielding effect // Vestnik gosudarstvennogo universiteta morskogo i rechnogo flota im. adm. S.O. Makarova. – 2016. – 2(36). – P. 127-137 (in Russian).
