РЕШЕНИЕ ОБРАТНОЙ СМЕШАННОЙ КРАЕВОЙ ЗАДАЧИ АЭРОГИДРОДИНАМИКИ РЕШЁТОК
РЕШЕНИЕ ОБРАТНОЙ СМЕШАННОЙ КРАЕВОЙ ЗАДАЧИ АЭРОГИДРОДИНАМИКИ РЕШЁТОК
Научная статья
Салимов Р.Б.1, Горская Т.Ю.2, *
1 ORCID: 0000-0003-4177-4830;
2 ORCID: 0000-0001-7136-8388;
1, 2 Казанский государственный архитектурно-строительный университет, Казань, Россия
* Корреспондирующий автор (gorskaya0304[at]mail.ru)
АннотацияРассматривается обратная смешанная краевая задача аэрогидродинамики решёток, в которой требуется найти форму части профиля решётки по заданному по этой части распределению величины скорости и распределение величины скорости на остальной известной части профиля решётки, обтекаемой потенциальным потоком несжимаемой невязкой жидкости. Подробно рассматривается случай, когда искомый профиль близок к профилю известной решётки с известным комплексным потенциалом течения. Принимается, что известна часть нижней поверхности исследуемого профиля, за исключением его участка, прилегающего к носику профиля, а форма всей остальной части исследуемого профиля отыскивается по заданному на ней распределению величины скорости как функции дуговой абсциссы точки искомого профиля. Получены формулы, дающие решение поставленной задачи. В процессе решения задачи определяются период решётки и скорость потока, обтекающего решётку.
Ключевые слова: обратная смешанная краевая задача, аэрогидродинамика решётки, профиль, комплексный потенциал.
SOLVING THE INVERSE MIXED BOUNDARY VALUE PROBLEM OF LATTICE FLUID DYNAMICS
Research article
Salimov R.B.1, Gorskaia T.Yu.2, *
1 ORCID: 0000-0003-4177-4830;
2 ORCID: 0000-0001-7136-8388;
1, 2 Kazan State University of Architecture and Engineering, Kazan, Russia
* Corresponding author (gorskaya0304[at]mail.ru)
AbstractThe authors consider the inverse mixed boundary value problem of lattice fluid dynamics, in which we need to find the shape of a part of the lattice profile through the velocity distribution given for this part and the velocity distribution on the rest known part of the lattice profile, which is streamlined by a potential flow of ideal frictionless liquid. The authors delve into the case when the required profile is close to the profile of a known lattice with a known flow complex potential. It is assumed that the known part of the lower surface of the profile, except for its plot adjacent to the nose profile, and the form of the rest of the investigated profile is sought, through the distribution of velocity as a function of the arc abscissa of the point of the required profile. We obtained formulas giving a solution to the problem. In the process of solving the problem, the lattice period and the flow velocity streamlining the lattice are determined.
Keywords: inverse mixed boundary value problem, lattice fluid dynamics, profile, complex potential.
ВведениеПусть в плоскости комплексного переменного z = x + iy расположена решётка профилей, период которой равен ![]() ([1], стр. 123),
([1], стр. 123), ![]() ([2], стр. 291), Решётка обтекается установившимся потоком несжимаемой невязкой жидкости, комплексный потенциал его обозначается w(z). Значение комплексной скорости w’(z) на бесконечности слева от решётки обозначим через
([2], стр. 291), Решётка обтекается установившимся потоком несжимаемой невязкой жидкости, комплексный потенциал его обозначается w(z). Значение комплексной скорости w’(z) на бесконечности слева от решётки обозначим через ![]() справа от решётки – через
справа от решётки – через ![]() Поток, обтекающий решётку, имеет период, равный
Поток, обтекающий решётку, имеет период, равный ![]()
Обозначим через Lz профиль решётки, точка разветвления на котором совпадает с точкой z = 0.
Введём плоскость комплексного переменного ![]()
![]() и функцией
и функцией ![]() отобразим конформно внешность решётки профилей на бесконечнолистную риманову поверхность внутри системы концентрических окружностей, имеющих уравнение
отобразим конформно внешность решётки профилей на бесконечнолистную риманову поверхность внутри системы концентрических окружностей, имеющих уравнение ![]() требуя, чтобы бесконечно удалённым точкам слева и справа от решётки отвечали точки соответственно
требуя, чтобы бесконечно удалённым точкам слева и справа от решётки отвечали точки соответственно ![]() эта функция отображает конформно круг
эта функция отображает конформно круг ![]() с разрезом по отрезку, соединяющему точки
с разрезом по отрезку, соединяющему точки ![]() на область, ограниченную профилем решётки и двумя конгруэнтными линиями, причём разность комплексных координат соответственных точек линии, лежащей выше профиля, и линии, расположенной ниже профиля, равна
на область, ограниченную профилем решётки и двумя конгруэнтными линиями, причём разность комплексных координат соответственных точек линии, лежащей выше профиля, и линии, расположенной ниже профиля, равна ![]() ([1], стр. 123).
([1], стр. 123).
В дальнейшем будем рассматривать ветвь ![]() которая окружность
которая окружность ![]() переводит в профиль Lz.
переводит в профиль Lz.
Обозначим
где B1 - действительное число, ![]() причём
причём ![]() точки окружности
точки окружности ![]() отвечающие соответственно точке разветвления A и точке схода B потока на профиле Lz решётки.
отвечающие соответственно точке разветвления A и точке схода B потока на профиле Lz решётки.
На профиле Lz и на окружности ![]() установим направление, при котором область течения остаётся слева.
установим направление, при котором область течения остаётся слева.
Циркуляция Г скорости по окружности ![]() с указанным направлением будет равна ([1], стр. 141)
с указанным направлением будет равна ([1], стр. 141)
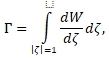 (3)
такой же будет и циркуляция скорости по Lz.
С учётом формул (2), (3) получим
(3)
такой же будет и циркуляция скорости по Lz.
С учётом формул (2), (3) получим
Производная ![]() аналитична в круге
аналитична в круге ![]() и в точках
и в точках ![]() , принимает значения соответственно
, принимает значения соответственно ![]() . Согласно (1)
. Согласно (1) ![]() , поэтому в силу (2) в окрестностях точек
, поэтому в силу (2) в окрестностях точек ![]() , будут справедливы разложения соответственно
, будут справедливы разложения соответственно
![]() (5)
(5)
![]() (6)
(6)
где
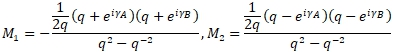 (7)
(7)
![]() (8)
(8)
Функция ![]() получает приращение, равное
получает приращение, равное ![]() при обходе (против хода часовой стрелки) окружности малого радиуса ε с центром в точке
при обходе (против хода часовой стрелки) окружности малого радиуса ε с центром в точке ![]() начиная от точки, лежащей на верхнем берегу разреза, проведённого по отрезку, соединяющему точки
начиная от точки, лежащей на верхнем берегу разреза, проведённого по отрезку, соединяющему точки ![]() С другой стороны согласно (5) это приращение равно
С другой стороны согласно (5) это приращение равно ![]() . Поэтому имеет место соотношение
. Поэтому имеет место соотношение
равносильна системе (11) и, следовательно, системе (9), (10), где ![]()
Пусть ![]() есть потенциал скорости на окружности
есть потенциал скорости на окружности ![]() для вышеуказанного течения в области
для вышеуказанного течения в области ![]() удовлетворяющий условию
удовлетворяющий условию ![]() Замечая, что
Замечая, что
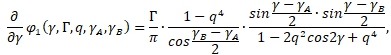 (14)
(14)
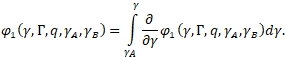 (15)
(15)
Постановка задачи. Некоторые предварительные соотношения
Пусть s – дуговая абсцисса точки профиля Lz, отсчитываемая от точки разветвления A потока на профиле в указанном выше направлении (при котором область течения остаётся слева), l – периметр профиля Lz, s = sB – дуговая абсцисса точки схода B потока на Lz, причём точка B совпадает с задней кромкой профиля Lz, и A – точка примыкающей к передней кромке Lz дуги нижней поверхности профиля Lz.
Примем ![]() величина скорости, α – угол, образованный с действительной осью скорости в точке z.
величина скорости, α – угол, образованный с действительной осью скорости в точке z.
Рассмотрим решение следующей задачи. Форма дуги AB (содержащей верхнюю поверхность Lz) неизвестна, на ней задано распределение скорости![]() а форма остальной части BA профиля Lz известна, т. е. известна функция
а форма остальной части BA профиля Lz известна, т. е. известна функция ![]() . Требуется найти форму дуги AB и распределение скорости на известной дуге профиля Lz:
. Требуется найти форму дуги AB и распределение скорости на известной дуге профиля Lz: ![]() . Подлежат определению также период решётки
. Подлежат определению также период решётки ![]() скорости
скорости ![]() . Примем, что заданные функции
. Примем, что заданные функции ![]() дифференцируемы в интервалах соответственно
дифференцируемы в интервалах соответственно ![]() причём
причём ![]() .
.
Задача, аналогичная приведённой выше и сформулированная для случая изолированного профиля, исследовалась в работах ряда авторов. Краткий обзор указанных работ содержится в книге [3], посвящённой обратным краевым задачам аэрогидродинамики.
В то же время отсутствуют опубликованные научные статьи, посвящённые решению рассматриваемой задачи для гидродинамических решёток.
Из соответствия точек Lz и окружности ![]() при конформном отображении функцией
при конформном отображении функцией ![]() определяется зависимость
определяется зависимость ![]() . При этом
. При этом
есть однозначная аналитическая в круге ![]() функция, значения которой на окружности
функция, значения которой на окружности ![]() вычислены в предположении, что
вычислены в предположении, что
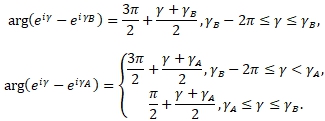 Здесь имеем
Здесь имеем
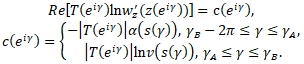 (17)
Следовательно, для аналитической в круге
(17)
Следовательно, для аналитической в круге 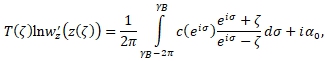
где ![]() - действительная постоянная. Переходя в этой формуле к пределу при
- действительная постоянная. Переходя в этой формуле к пределу при ![]() когда и левая часть формулы стремится к нулю, будем иметь ([4], с. 59)
когда и левая часть формулы стремится к нулю, будем иметь ([4], с. 59)
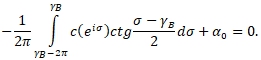 Поэтому предыдущая формула может быть записана так
Поэтому предыдущая формула может быть записана так
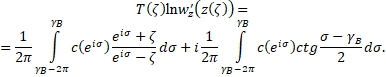 (18)
Переходя здесь к пределу при
(18)
Переходя здесь к пределу при 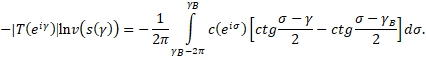 (19)
(19)
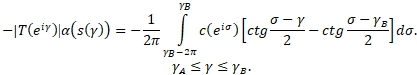 (20)
Полагая
(20)
Полагая 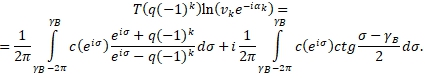 (21)
Пусть
(21)
Пусть 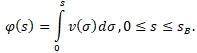 (22)
Положим
(22)
Положим 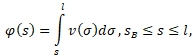 (23)
причём
(23)
причём 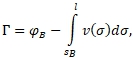 (24)
(24)
где ![]() - известная величина, определяемая по формуле (22) при
- известная величина, определяемая по формуле (22) при ![]() - величина, выражение для которой находится на основании (19).
- величина, выражение для которой находится на основании (19).
Принимая во внимание (14), (15), согласно (1) имеем
Соотношения (13), (24), (25), (26), (19), (21) равносильны системе 10 действительных уравнений с неизвестными ![]() (Подставляя выражения для
(Подставляя выражения для ![]() при
при ![]() согласно соответственно (24), (19), (21), указанную систему можно привести к системе четырёх действительных уравнений с неизвестными
согласно соответственно (24), (19), (21), указанную систему можно привести к системе четырёх действительных уравнений с неизвестными ![]() .
.
При найденных названных величинах период решётки ![]() определяется по формуле (12).
определяется по формуле (12).
Вычислив ![]() по формуле (20), находим координаты точек искомой дуги
по формуле (20), находим координаты точек искомой дуги
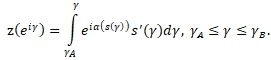 (27)
(27)
В силу (12), (13) контур Lz будет замкнутым. Используя формулу (19) определим распределение скорости на известной части BA профиля Lz ![]() при найденных
при найденных ![]()
Приближённое решение задачи
Для решения вышеуказанной системы с неизвестными величинами и функцией ![]() можно использовать различные методы, в частности, методы последовательных приближений. Для простоты остановимся на случае, когда заданное на искомом участке профиля решётки распределение скорости близко к распределению скорости на соответствующем участке известного профиля некоторой исходной решётки, когда разности указанных скоростей в соответствующих точках профилей и разности координат соответствующих точек остальных участков профилей являются малыми величинами и величины второго порядка относительно этих малых можно не учитывать.
можно использовать различные методы, в частности, методы последовательных приближений. Для простоты остановимся на случае, когда заданное на искомом участке профиля решётки распределение скорости близко к распределению скорости на соответствующем участке известного профиля некоторой исходной решётки, когда разности указанных скоростей в соответствующих точках профилей и разности координат соответствующих точек остальных участков профилей являются малыми величинами и величины второго порядка относительно этих малых можно не учитывать.
Для величин, относящихся к исходной известной решётки, сохраним принятые выше обозначения, а соответствующие величины, относящиеся к искомой изменённой решётке, будем обозначать теми же буквами, снабжая их верхней волнистой чертой. Будем считать, что для исходной решётки функции ![]() известны.
известны.
Для простоты примем, что ![]()
Пусть распределение скорости на искомом участке ![]() профиля
профиля ![]() изменённой решётки задано в виде
изменённой решётки задано в виде
где ![]() - известное распределение скорости на дуге AB профиля Lz исходной известной решётки,
- известное распределение скорости на дуге AB профиля Lz исходной известной решётки, ![]() - дифференцируемы в интервале
- дифференцируемы в интервале ![]() малая положительная величина, причём величинами порядка
малая положительная величина, причём величинами порядка ![]() можно пренебречь,
можно пренебречь, ![]()
Примем, что для величин ![]() остальных участков
остальных участков ![]() справедливо соотношение, аналогичное (28)
справедливо соотношение, аналогичное (28)
в котором ![]() функция, дифференцируемая в интервале
функция, дифференцируемая в интервале ![]()
Будем считать также, что профиль ![]() обладает достаточной степенью гладкости и производная
обладает достаточной степенью гладкости и производная ![]() удовлетворяет условию Гельдера всюду на окружности
удовлетворяет условию Гельдера всюду на окружности ![]() ([5], с. 117)
([5], с. 117)
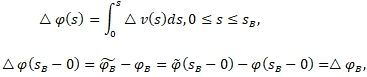 (30)
причём в силу (30), (28)
(30)
причём в силу (30), (28)
Если записать формулу, аналогичную (19) для величин на ![]() то в ней величины
то в ней величины ![]() отвечающие соответственно
отвечающие соответственно ![]() будут неизвестны, и по ней не удастся найти значения
будут неизвестны, и по ней не удастся найти значения ![]() на известной части
на известной части ![]() профиля
профиля ![]() .
.
В связи с этим рассмотрим формулы, получаемые из (19), (20) с учётом (17) заменой ![]() соответственно на
соответственно на ![]() и когда вместо
и когда вместо ![]() формулы (17) берётся
формулы (17) берётся
![]() (32)
(32)
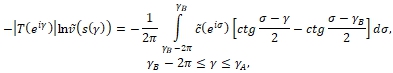 (33)
(33)
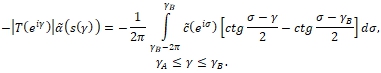 (34)
(34)
По формуле (33) определим распределение скорости ![]() на известном участке
на известном участке ![]() в первом приближении.
в первом приближении.
На основании формул, аналогичных (23), (24), (в первом приближении) будем иметь
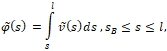 причём
причём 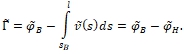 Принимая во внимание (28), (29) и формулы (17), (32), заключаем, что
Принимая во внимание (28), (29) и формулы (17), (32), заключаем, что 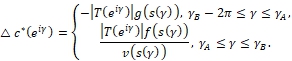
Тогда на основании соотношения, полученного из (33) вычитанием соответствующих частей (19), замечая, что с принятой точностью ![]() приходим к выводу, что
приходим к выводу, что ![]() где
где
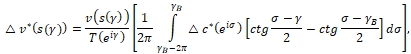
Здесь надо учесть известные результаты, относящиеся к поведению сингулярных интегралов вблизи разрыва плотности ([6], с. 58, 75, 95), а также аналогичные результаты работы [7].
Поэтому для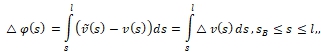 (35)
Имеем
(35)
Имеем
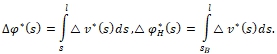 Из формулы, аналогичной (26),
Из формулы, аналогичной (26),
Примем, что здесь ![]() есть малые величины
есть малые величины ![]() . Так как частные производные второго порядка функции
. Так как частные производные второго порядка функции ![]() непрерывны, то согласно формуле Тейлора разность правой части предыдущей формулы мало отличается от первого дифференциала этой функции в силу вышеуказанных условий. Поэтому указанную формулу (40)
непрерывны, то согласно формуле Тейлора разность правой части предыдущей формулы мало отличается от первого дифференциала этой функции в силу вышеуказанных условий. Поэтому указанную формулу (40) ![]() для можно записать так
для можно записать так
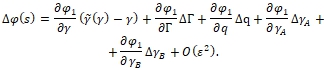 (41)
Здесь
(41)
Здесь 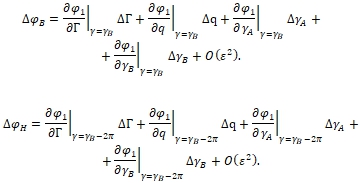 (42)
Формулу (41) с учётом последних выражений для
(42)
Формулу (41) с учётом последних выражений для 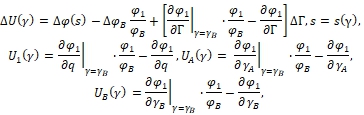
при ![]() в последних четырёх формулах
в последних четырёх формулах ![]() надо заменить на
надо заменить на ![]() условие
условие ![]() – на условие
– на условие
В силу (31), (36), (37) для множителя ![]() формулы (43) имеем
формулы (43) имеем
В силу условий, которым удовлетворяют ![]() для которой справедлива формула (43), дифференцируема в интервалах
для которой справедлива формула (43), дифференцируема в интервалах ![]()
![]() и имеет производную, удовлетворяющую условию Гельдера всюду в этих интервалах. На концах интервалов
и имеет производную, удовлетворяющую условию Гельдера всюду в этих интервалах. На концах интервалов ![]() обращается в нуль. Нетрудно проверить, что делённые на
обращается в нуль. Нетрудно проверить, что делённые на ![]() слагаемые порядка
слагаемые порядка ![]() формулы Тейлора, неучтённые в формуле (43), при нахождении
формулы Тейлора, неучтённые в формуле (43), при нахождении ![]() приводят к величинам
приводят к величинам ![]() Согласно (43), (44) имеем
Согласно (43), (44) имеем
Чтобы найти значение ![]() в первом приближении по аналогии с предыдущим воспользуемся формулой, получаемой из (18) заменой
в первом приближении по аналогии с предыдущим воспользуемся формулой, получаемой из (18) заменой ![]() на функцию (32). Полагая в полученной формуле
на функцию (32). Полагая в полученной формуле ![]() будем иметь
будем иметь
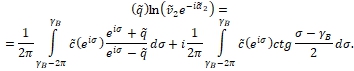 (45)
Примем, что
(45)
Примем, что 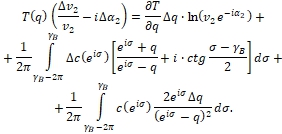 (46)
Поступая совершенно аналогично в случае
(46)
Поступая совершенно аналогично в случае 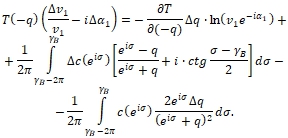 (47)
(47)
Интеграл с плотностью ![]() формулы (46) обозначим
формулы (46) обозначим ![]() и сумму слагаемых этой формулы, содержащих
и сумму слагаемых этой формулы, содержащих ![]() обозначим
обозначим ![]() . Тогда формулы (46), (47) примут вид
. Тогда формулы (46), (47) примут вид
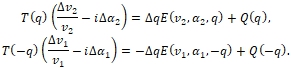 Уравнения (13) запишем так
Уравнения (13) запишем так
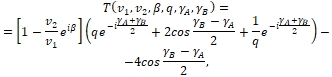 (49)
(49)
Отсюда вычтем почленно равенство (48). Разность в левой части с принятой точностью заменим первым дифференциалом функции (49) и придём к уравнению
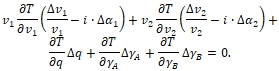 Подставим сюда выражения из (46), (47) для
Подставим сюда выражения из (46), (47) для 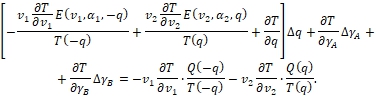 (50)
(50)
Соотношения (42) (без слагаемого ![]() и (50) представляют собой систему уравнений с неизвестными
и (50) представляют собой систему уравнений с неизвестными ![]() Остановимся лишь на общем случае, когда определитель системы отличен от нуля и система имеет единственное решение. Определив из неё величины
Остановимся лишь на общем случае, когда определитель системы отличен от нуля и система имеет единственное решение. Определив из неё величины ![]() из (47) найдем
из (47) найдем ![]() , затем из (46) – величины
, затем из (46) – величины ![]()
На основании формулы (12) находится период решётки ![]() Формулы (39), (43) определяют зависимость
Формулы (39), (43) определяют зависимость ![]() эта зависимость вместе с функцией
эта зависимость вместе с функцией ![]() отвечает найденным
отвечает найденным ![]()
Если в рамках принятой точности ![]() в частности
в частности ![]() то найденная по формуле (33) функция
то найденная по формуле (33) функция ![]() принимается за искомое распределение скорости на известной части
принимается за искомое распределение скорости на известной части ![]() функцию
функцию ![]() определяемую по формуле (34) примем за искомую функцию, по значениям которой вычисляются координаты неизвестной дуги
определяемую по формуле (34) примем за искомую функцию, по значениям которой вычисляются координаты неизвестной дуги ![]() профиля
профиля ![]() на основании формулы, аналогичной (27).
на основании формулы, аналогичной (27).
Если высказанное не имеет места, то выкладки, аналогичные вышеуказанным, проводятся во втором приближении. Для этого в формулах, использованных в первом приближении, зависимость ![]() и связанные с ней параметры
и связанные с ней параметры ![]() заменяются на соответственно найденную в первом приближении
заменяются на соответственно найденную в первом приближении ![]() и связанные с ней параметры
и связанные с ней параметры ![]()
![]() и определяется зависимость
и определяется зависимость ![]() во втором приближении и т. д., зная зависимость
во втором приближении и т. д., зная зависимость ![]() и связанные с ней параметры, определим зависимость
и связанные с ней параметры, определим зависимость ![]() и соответствующие ей параметры. Если
и соответствующие ей параметры. Если ![]() с принятой точностью, то, по формулам, получаемым из (33), (34) аналогичной вышеуказанной заменой, вычислим искомую скорость
с принятой точностью, то, по формулам, получаемым из (33), (34) аналогичной вышеуказанной заменой, вычислим искомую скорость ![]() на известной части
на известной части ![]() профиля
профиля ![]() и функцию
и функцию ![]() для искомого участка
для искомого участка ![]() контура
контура ![]() по которой вычисляются координаты точек дуги
по которой вычисляются координаты точек дуги ![]() с использованием формулы, аналогичной (27).
с использованием формулы, аналогичной (27).
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Седов Л.И. Плоские задачи гидродинамики и аэродинамики / Л.И. Седов. – М.: Наука, 1980. – 448 с.
- Кочин Н.Е. Теоретическая гидродинамика / Н.Е. Кочин, И.А. Кибель, Н.В. Розе. – М.: ГИФМЛ, 1963. – 583 с.
- Елизаров А.М. Обратные краевые задачи аэрогидродинамики / А.М. Елизаров, Н.Б. Ильинский, А.В. Поташов. –М.: Наука. 1994. – 440 с.
- Гахов Ф.Д. Краевые задачи / Ф.Д. Гахов. – М.: Наука, 1977. – 641 с.
- Лаврентьев М.А. Методы теории функций комплексного переменного / М.А. Лаврентьев, Б.В. Шабат. – М.: Наука. 1973. – 736 с.
- Мусхелишвили Н.И. Сингулярные интегральные уравнения / Н.И. Мусхелишвили. – М.: ГИФМЛ, 1962. – 583 с.
- Салимов Р.Б. К вычислению сингулярных интергалов с ядром Гильберта / Р.Б. Салимов // Известия вузов. Математика. 1970, №12 – С. 93-96.
Список литературы на английском языке / References in English
- Sedov L.I. Plosskiye zadahi gidrodinamiki I aerodinamiki [Plane problems of hydrodynamics and aerodynamics] / L.I. Sedov. - : Science. 1980. - 448 p. [in Russian]
- Kochin N.E. Teoreticheskaya gidromehanika [Theoretical fluid mechanics] / N.E. Kochin, I.A. Kibel, N.V. Roze. - : GIFML. 1963. - 583 p. [in Russian]
- Elizarov A.M. Obratnyi kraevie zadachi aerogidrodinamyki [Reverse regional tasks of aerodynamics] / A.M. Elizarov, N.B. Ilyinsky, A.V. Potashov. -M.: Science. - 440 p. [in Russian]
- Gahov F.D. Kraevye zadachi. [Boundary value problems] M.: Nauka, 1977. – 641 p. [in Russian]
- Lavrent’ev M.A. Metody teorii funkchiy komplexnogo peremennogo [Methods of the theory of functions of a complex variable] : Nauka, 1973. – 736 p. [in Russian]
- Myshelishvyly N.I. Singulyrniye integral’nye uravnenia [Singular integral equations] - M.: GIFML. - 583 p. [in Russian]
- Salimov R.B. K vychisleniu singulyrnikh integralov s yadrom Hilberta [To the calculation of singular intergals with the core of Hilbert] / R.B. Salimov // Izvestia of universities. 1970, No.12 - P. 93-96. [in Russian]
