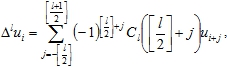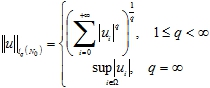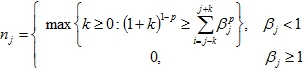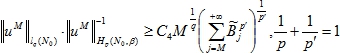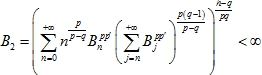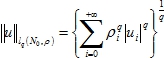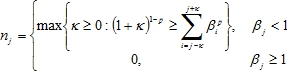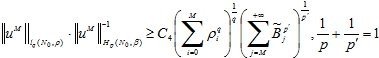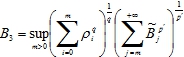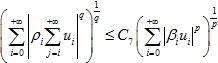РАЗНОСТНЫЕ ВЕСОВЫЕ ТЕОРЕМЫ ВЛОЖЕНИЯ В ОДНОМ ВЫРОЖДЕННОМ СЛУЧАЕ
Мустафина Л.М.1, Журов В.В.2, Абаева Н.Ф.3, Ахметов К.М.4
1 Кандидат физико-математических наук, доцент,
2 Кандидат технических наук, старший преподаватель,
3 Кандидат педагогических наук, старший преподаватель,
4 Кандидат технических наук, старший преподаватель,
1,2,3,4 Карагандинский государственный технический университет, Караганда, Казахстан
РАЗНОСТНЫЕ ВЕСОВЫЕ ТЕОРЕМЫ ВЛОЖЕНИЯ В ОДНОМ ВЫРОЖДЕННОМ СЛУЧАЕ
Аннотация
Статья посвящена изучению условий вложения пространства ![]() в пространство
в пространство ![]() . Здесь
. Здесь ![]() разностный аналог весового лебегова пространства, в котором последовательность ρ играет роль веса. Пространство
разностный аналог весового лебегова пространства, в котором последовательность ρ играет роль веса. Пространство ![]() определяется как пополнение множества финитных последовательностей по норме. Для доказательства основного утверждения на вес β накладываются дополнительные условия. Дискретный вариант усреднения М. Отелбаева является эффективным инструментом при исследовании вопросов о разностных теоремах вложения, свойствах разностных операторов и т. п. Используя различные виды дискретных усреднений, исследуются вопросы теории вложения пространств с дискретным аргументом, а также получены двусторонние оценки норм операторов вложения и оценки аппроксимативных чисел оператора вложения.
определяется как пополнение множества финитных последовательностей по норме. Для доказательства основного утверждения на вес β накладываются дополнительные условия. Дискретный вариант усреднения М. Отелбаева является эффективным инструментом при исследовании вопросов о разностных теоремах вложения, свойствах разностных операторов и т. п. Используя различные виды дискретных усреднений, исследуются вопросы теории вложения пространств с дискретным аргументом, а также получены двусторонние оценки норм операторов вложения и оценки аппроксимативных чисел оператора вложения.
Ключевые слова: разностные теоремы вложения, весовое лебегово пространство, пополнение множества финитных последовательностей.
Mustafina L.M.1, Zhurov V.V.2, Abaeva N.F.3, Akhmetov K.M.4
1 PhD in Physics and Mathematics, Associate professor,
2 PhD in Physics and Mathematics, Senior Lecturer,
3 PhD in Pedagogy, Senior Lecturer,
4 PhD in Engineering, Senior Lecturer,
1,2,3,4 Karaganda State Technical University, Karaganda, Kazakhstan
DIFFERENTIAL WEIGHTS EMBEDDING THEOREM IN ONE DEGENERATED CASE
Abstract
The article is devoted to the study of the conditions for embedding of the space ![]() to space
to space ![]() . Here
. Here ![]() is the difference analog of a weighted Lebesgue space in which the sequence plays the role of weight. Space is defined as the completion of the set of finite sequences by the norm. In order to prove the main assertion, additional conditions are imposed on the weight. What a discrete version of M. Otelbaev's averaging is an effective tool in the study of questions on difference embedding theorems, properties of difference operators, etc. Using various types of discrete averages, the questions of embedding theory of spaces with a discrete argument are investigated, as well as bilateral estimates of the norms of the embedding and estimation operators approximate numbers of the embedding operator.
is the difference analog of a weighted Lebesgue space in which the sequence plays the role of weight. Space is defined as the completion of the set of finite sequences by the norm. In order to prove the main assertion, additional conditions are imposed on the weight. What a discrete version of M. Otelbaev's averaging is an effective tool in the study of questions on difference embedding theorems, properties of difference operators, etc. Using various types of discrete averages, the questions of embedding theory of spaces with a discrete argument are investigated, as well as bilateral estimates of the norms of the embedding and estimation operators approximate numbers of the embedding operator.
Keywords: embedding difference theorems, weighted Lebesgue space, completion of a set of finite sequences.
Пространства с весом естественным образом возникают при рассмотрении дифференциальных уравнений с переменными коэффициентами. Свойства (теоремы вложения) весовых пространств рассматривались в работах 1-13. В работе М. Отелбаева [13] теоремы вложения применяются к изучению спектральных вопросов полуограниченных операторов. Результаты этой работы обобщают известные теоремы компактности оператора вложения, полученные в работе Молчанова А.М. [14], а также в работах Бирмана М.Ш. и Павлова Б.С. [7], Мазьи В.Г. [8], Мазьи В.Г. и М. Отелбаева [10]. Усреднения весовых функций, впервые введенные М. Отелбаевым в [11], и усовершенствованные им же в [12], [13], позволяют получить двусторонние оценки норм некоторых операторов вложения, критерии дискретности спектра и оценки функций распределения спектра некоторых полуограниченных операторов.
В отличие от теорем вложения функций непрерывного аргумента, аппарат которых хорошо развит, теоремы вложения функций дискретного аргумента (разностные теоремы вложения) изучены слабее. Но применение методов конечных разностей для решения дифференциальных уравнений с переменными коэффициентами требует использования различных априорных оценок, этим объясняется интерес к разностным теоремам вложения. Исследование разностных теорем вложения началось, по-видимому, с работы С.Л. Соболева [15], в которой были получены оценки некоторых сумм, заданных на сетке. Как показали исследования, проведенные в этом направлении, дискретный вариант усреднения М. Отелбаева является эффективным инструментом при изучении вопросов о разностных теоремах вложения, свойствах разностных операторов и т.п. В данной работе, используя различные виды дискретных усреднений, исследованы вопросы теории вложения пространств с дискретным аргументом, получены двусторонние оценки норм операторов вложения. Особый интерес приобретают весовые пространства и изучение разностных теорем вложения пространств с весом. Применение разностных теорем вложения и получение оценок аппроксимативных чисел является одной из важных задач приближенного вычисления, а также используются при исследовании устойчивости разностных схем, в спектральной теории матриц.
В данной работе приводятся некоторые разностные теоремы для пространств с нормами, заведомо являющимися полунормами на нефинитных последовательностях.
Введем необходимые обозначения и определения.
Пусть ![]() - множество целых неотрицательных чисел,
- множество целых неотрицательных чисел, ![]() - последовательность действительных чисел. Для произвольного целого положительного числа l определим симметрическую разность l-го порядка, взятую в точке i, соотношением
- последовательность действительных чисел. Для произвольного целого положительного числа l определим симметрическую разность l-го порядка, взятую в точке i, соотношением
где ![]() - биномиальные коэффициенты, символ
- биномиальные коэффициенты, символ ![]() означает целую часть.
означает целую часть.
Будем говорить, что последовательность ![]() принадлежит пространству
принадлежит пространству ![]() если конечна норма
если конечна норма
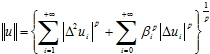 (1)
где
(1)
где соответственно разности первого и второго порядков; ![]()
Обозначим через ![]() пополнение множества финитных последовательностей по норме (1),
пополнение множества финитных последовательностей по норме (1), ![]() играет роль веса.
играет роль веса.
В работе [16, С. 122] получено вложение пространства с весом ![]() в пространство
в пространство ![]() - разностный аналог, рассмотренных М. Отелбаевым в [12], пространств
- разностный аналог, рассмотренных М. Отелбаевым в [12], пространств ![]() . Значительная трудность исследования этих вложений связана с тем, что норма пространства
. Значительная трудность исследования этих вложений связана с тем, что норма пространства ![]() не содержит в явном виде самой последовательности
не содержит в явном виде самой последовательности ![]() . Относительно разностных теорем вложения можно отметить работу Г.Х Мухамедиева [18], хотя норма пространства
. Относительно разностных теорем вложения можно отметить работу Г.Х Мухамедиева [18], хотя норма пространства ![]() определялась только вторым слагаемым (1).
определялась только вторым слагаемым (1).
Двусторонние оценки выражения
совпадающие по порядку и критерий компактности оператора вложения ![]() и достаточные условия вложения пространства
и достаточные условия вложения пространства ![]() в пространство
в пространство ![]() сформулированы в терминах последовательности
сформулированы в терминах последовательности
где ![]() после четного продолжения последовательности
после четного продолжения последовательности ![]() на все множество Z, определяется следующим образом
на все множество Z, определяется следующим образом
Из определения ![]() следует, что при
следует, что при ![]() равенство
равенство ![]() в некоторой точке
в некоторой точке ![]() возможно лишь в случае
возможно лишь в случае ![]() , а при p=1 равенство
, а при p=1 равенство ![]() означает, что
означает, что ![]() . Следовательно, конечность
. Следовательно, конечность ![]() в одной точке из
в одной точке из ![]() эквивалентна конечности всюду в
эквивалентна конечности всюду в ![]() . Кроме того условие
. Кроме того условие ![]() для всех
для всех ![]() при
при ![]() эквивалентно требованию
эквивалентно требованию ![]() а при p=1 - требованию
а при p=1 - требованию ![]() .
.
Оценка сверху нормы оператора ![]() выводится из локальных оценок, оценка снизу в случае
выводится из локальных оценок, оценка снизу в случае ![]() получается с помощью построения пробной последовательности, описанной в лемме 1.
получается с помощью построения пробной последовательности, описанной в лемме 1.
Лемма 1. Если ![]() , то найдется последовательность
, то найдется последовательность ![]() при
при ![]() и такая, что
и такая, что
если ![]() , где С4 не зависит от M, R – любое достаточно большое число.
, где С4 не зависит от M, R – любое достаточно большое число.
Имеют место теоремы
Теорема 1
Пусть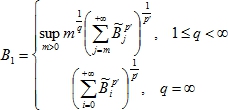 причем для оператора вложения
причем для оператора вложения где C1 и C2 постоянные зависящие только от p и q.
Теорема 2
Пусть ![]() . Тогда пространство
. Тогда пространство ![]() компактно вложено в пространство
компактно вложено в пространство ![]() тогда и только тогда, когда выполняется условие
тогда и только тогда, когда выполняется условие
Можно привести примеры весовых последовательностей, для которых имеет место вложение пространства ![]() в пространство
в пространство ![]() . Например, полагая
. Например, полагая ![]() , получим, что пространство
, получим, что пространство ![]() вложено в пространство
вложено в пространство ![]() тогда и только тогда, когда
тогда и только тогда, когда
В случае ![]() пространство
пространство ![]() вложено в пространство
вложено в пространство ![]() тогда и только тогда, когда
тогда и только тогда, когда
б) ![]() при всех стальных значениях p и q.
при всех стальных значениях p и q.
Пространство ![]() компактно вложено в пространство
компактно вложено в пространство ![]() при
при ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]()
Рассмотрим пространство ![]() - разностный аналог весового лебегова пространства, которое определяется как множество всех последовательностей
- разностный аналог весового лебегова пространства, которое определяется как множество всех последовательностей ![]() имеющих конечную норму:
имеющих конечную норму:
здесь последовательность ![]() играет роль веса, причем
играет роль веса, причем ![]() .
.
На множестве финитных последовательностей ![]() можно определить норму (1), где
можно определить норму (1), где ![]() - последовательность неотрицательных чисел,
- последовательность неотрицательных чисел, ![]()
соответственно разности первого и второго порядков; ![]() .
.
![]() - пополнение множества финитных последовательностей по норме (1). Нулем пространства
- пополнение множества финитных последовательностей по норме (1). Нулем пространства ![]() может оказаться класс, состоящий из констант (например, при
может оказаться класс, состоящий из констант (например, при ![]() ) или линейных последовательностей (при
) или линейных последовательностей (при ![]() ). В таком случае вложение
). В таком случае вложение ![]() в пространство
в пространство ![]() возможно лишь при
возможно лишь при ![]() . Норму (1) называют вырожденной, имея в виду возможность такой патологии. На вес накладываются дополнительные условия, при которых нулем в пространстве
. Норму (1) называют вырожденной, имея в виду возможность такой патологии. На вес накладываются дополнительные условия, при которых нулем в пространстве ![]() является класс последовательностей, обращающихся в ноль почти всюду.
является класс последовательностей, обращающихся в ноль почти всюду.
Продолжая ![]() четно на все множество целых чисел, обозначим
четно на все множество целых чисел, обозначим
Из определения последовательности чисел ![]() следует, что
следует, что ![]() только при
только при ![]() и условие
и условие ![]() эквивалентно требованию:
эквивалентно требованию: ![]() .
.
Обозначим ![]() - отрезок, аналогично
- отрезок, аналогично ![]() Норма пространства
Норма пространства ![]() на этих отрезках определяется так:
на этих отрезках определяется так:
Введенная выше последовательность ![]() обладает важным свойством, сформулируем его в виде леммы.
обладает важным свойством, сформулируем его в виде леммы.
Лемма 2. Пусть ![]() определена соотношением (2). Тогда для всех
определена соотношением (2). Тогда для всех ![]() выполняется неравенство
выполняется неравенство ![]() .
.
Приведем ряд утверждений, с помощью которых будут доказаны теоремы вложения.
Лемма 3. Пусть вес ![]() удовлетворяет условию:
удовлетворяет условию: ![]() - отрезки, определенные выше и
- отрезки, определенные выше и ![]() определено соотношением (2). Тогда существует последовательность чисел
определено соотношением (2). Тогда существует последовательность чисел ![]() такая, что
такая, что
Доказательство см., например, в работе [17, С. 240].
Кроме приведенных утверждений, в доказательстве теорем вложения используется, так называемая, пробная последовательность, удовлетворяющая определенным условиям. Существование такой пробной последовательности доказывается в лемме:
Лемма 4. Если ![]() , то найдется последовательность
, то найдется последовательность ![]() и такая, что
и такая, что
если ![]() , где С4 не зависит от M, R – любое достаточно большое число.
, где С4 не зависит от M, R – любое достаточно большое число.
Лемма 5. Для любой последовательности ![]() справедливо неравенство
справедливо неравенство ![]() .
.
На основании приведенных лемм 3 и 4 доказывается критерий вложения пространства ![]() в пространство
в пространство ![]() при
при ![]() и двусторонние оценки нормы оператора вложения
и двусторонние оценки нормы оператора вложения
Теорема 4
Пусть ![]() . Тогда пространство
. Тогда пространство ![]() вложено в пространство
вложено в пространство ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() , где
, где
Оценка сверху нормы оператора вложения Е2 и достаточное условие вложения пространств ![]() в
в ![]() доказывается из локальных оценок, в силу леммы 3 и справедливости следующей оценки:
доказывается из локальных оценок, в силу леммы 3 и справедливости следующей оценки:
Лемма 5. Если ![]() - последовательности неотрицательных чисел, то существует конечная постоянная С4
- последовательности неотрицательных чисел, то существует конечная постоянная С4
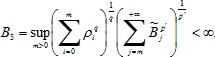 Кроме того наилучшая постоянная С7 связана с B3 соотношением:
Кроме того наилучшая постоянная С7 связана с B3 соотношением:
Список литературы / References
- Никольский С.М. Приближение функций многих переменных и теоремы вложения. – М.: Наука, 1977.
- Кудрявцев Л.Д. Теоремы вложения для классов функций, определенных на всем пространстве или полупространстве. Ч.1.// Мат. Сб. – 1966. – Т.66(111). – № 4. – С. 616-639.
- Кудрявцев Л.Д. Теоремы вложения для классов функций, определенных на всем пространстве или полупространстве. Ч.2.// Мат. Сб. – 1966. – Т.70(112). – № 1. – С. 3-35.
- Лизоркин П.И. Граничные свойства функций из «весовых классов». // ДАН СССР. – 1960. – Т.132. – № 3. – С. 514-517.
- Бесов О.В. Исследование одного семейства функциональных пространств в связи с теоремами вложения и продолжения. // Тр.МИАН. – 1961. – Т.60. – С.42-81.
- Ильин В.П. Интегральное представление функций классов и теоремы вложения. // Зап.науч.семинаров Лен.отд. МИАН СССР. –1970. – Т.19. – С. 95-155.
- Бирман М.Ш. О полной непрерывности некотрых операторов вложения / Бирман М.Ш., Павлов Б.С. // Вест.ЛГУ. Сер.мат., мех. и астрономия. –1961. – Вып.1. – С.61-74.
- Мазья В.Г. О (p,l) – емкости, теоремах вложения и спектре сопряженного эллиптического оператора. // Изв.АН СССР. Сер.мат. – 1973. – Т.37. – С. 356-385.
- Лизоркин П.И. Теоремы вложения и компактности для пространств Соболевского типа с весами. Ч.1. / Лизоркин П.И., Отелбаев М. // Мат.сб. –1979. – Т.108. – №3. – С. 358-377.
- Мазья В.Г. О теоремах вложения и спектре одного псевдодифференциального оператора / Мазья В.Г., Отелбаев М. // Сиб.мат.жур. – 1977. – Т.18. – №5. – С.1073-1087.
- Отелбаев М. О природе спектра одномерных дифференциальных операторов // Вестн. МГУ.- Сер.1. Математика. Механика. – 1972. – №5. – С.43-51.
- Отелбаев М. Критерий дискретности спектра одного вырожденного оператора и некоторые теоремы вложения // Дифф.уравнения. – 1977. – Т.13, №1. – С.111-120.
- Отелбаев М. Теоремы вложения пространств с весом и их приложения к изучению спектра оператора Шредингера // Тр.МАИН. – 1979. – Т.150. – С.265-305.
- Молчанов А.М. Об условиях дискретности спектра самосопряженных дифференциальных уравнений второго порядка. // Тр.ММО. – 1953. – Т.2. – С. 169-200.
- Соболев С.Л. Об оценках некоторых сумм для функций, заданных на сетке. // Изв.АН СССР. Сер.мат. – 1940. – №4. – С.5-17.
- Мустафина Л.М. Разностные теоремы вложения пространств Соболева с весом / Мустафина Л.М., БулабаевА.Т // Всесоюзная школа молодых ученых: Тез. докл. – Ташкент. – 1988. – С. 121-122.
- Мынбаев К.Т. Весовые функциональные пространства и спектр дифференциальных операторов / МынбаевК.Т., Отелбаев М. // М.: Наука, 1988.
- Мухамедиев Г.Х. Плотность финитных функций и теоремы вложения для одного класса весовых пространств. // Дис…канд. физ.-мат. наук.- Баку. 1986.
Список литературы на английском языке / References in English
- Nikolsky S.M. Priblizheniye funktsiy mnogikh peremennykh i teoremy vlozheniya [Approximation of Functions of Several Variables and Embedding Theorems. – M.: Nauka, 1977. [in Russian]
- Kudryavtsev L.D. Teoremy vlozheniya dlya klassov funktsiy, opredelennykh na vsem prostranstve ili poluprostranstve. CH.1 [Embedding Theorems for Classes of Functions Defined on Entire Space or Half-space. Part 1.] / Mat. Col. 1966-66 (111). – №. 4. – P. 616-639. [in Russian]
- Kudryavtsev L.D. Teoremy vlozheniya dlya klassov funktsiy, opredelennykh na vsem prostranstve ili poluprostranstve. Ch.2 [Embedding Theorems for Classes of Functions Defined on Entire Space or Half-space. Part 2.] / Mat. Sat. – 1966 – T.70 (112). – № – P. 3-35. [in Russian]
- Lizorkin P.I. Granichnyye svoystva funktsiy iz «vesovykh klassov». [Boundary Properties of Functions from "Weight Classes"] // DAN SSSR. – 1960. – V.132. – № 3. – P. 514-517. [in Russian]
- Besov O.V. Issledovaniye odnogo semeystva funktsional'nykh prostranstv v svyazi s teoremami vlozheniya i prodolzheniya [Study of Family of Function Spaces in Connection with Embedding and Extension Theorems] // Tr. MIAN. – 1961. – V.60. – P.42-81. [in Russian]
- Ilyin V.P. Integral'noye predstavleniye funktsiy klassov i teoremy vlozheniya. [Integral Representation of Class Functions and Embedding Theorems] // Col of Scient seminars. Spb dep. Steklov Mathematical Institute of the USSR. –1970. – V.19. – P. 95-155. [in Russian]
- Birman M.Sh. O polnoy nepreryvnosti nekotrykh operatorov vlozheniya [On Complete Continuity of Some Embedding Operators / Birman M.Sh., Pavlov B.S. // Bul. of LSU. Math and ast. ser. – 1961. – Issue 1 –P0.61-74. [in Russian]
- Maz'ya V.G. O (p,l) – yemkosti, teoremakh vlozheniya i spektre sopryazhennogo ellipticheskogo operatora [On (p,l) – capacities, embedding theorems, and the spectrum of the conjugate elliptic operator.] // Bul of AS of the USSR. Math. Ser. – 1973. – V.37. – P. 356-385. [in Russian]
- Lizorkin P.I. Teoremy vlozheniya i kompaktnosti dlya prostranstv Sobolevskogo tipa s vesami. CH.1 [Embedding and Compactness Theorems for Spaces of Sobolev Type with Weights. Part 1.] / Lizorkin P.I., Otelbaev M. O. // Mat. – 1979. – V.108. – 3. – P. 358-377. [in Russian]
- Maz'ya V.G. O teoremakh vlozheniya i spektre odnogo psevdodifferentsial'nogo operatora [On Embedding Theorems and Spectrum of Pseudodifferential Operator] / Maz'ya VG, Otelbaev M. // Sib. math. jour. – 1977. – T.18. – № 5. – P.1073-1087 [in Russian]
- Otelbaev M. O prirode spektra odnomernykh differentsial'nykh operatorov [On nature of Spectrum of One-dimensional Differential Operators] / Bul of MSU – Ser.1. Mathematics. Mechanics. – 1972. – № – P.43-51. [in Russian]
- Otelbaev, M., Kriteriy diskretnosti spektra odnogo vyrozhdennogo operatora i nekotoryye teoremy vlozheniya [Criterion for Discreteness of Spectrum of Degenerate Operator, and Some Embedding Theorems] Diff. Equations. 1977. – V.13, № – P.111-120. [in Russian]
- Otelbaev M., Teoremy vlozheniya prostranstv s vesom i ikh prilozheniya k izucheniyu spektra operatora Shredingera [Embedding Theorems for Spaces with Weight and Their Applications to Study of Spectrum of Schrödinger operator, Tr. MAIN. – 1979. – Vol. 150, P. 265-305. [in Russian]
- Molchanov A.M. Ob usloviyakh diskretnosti spektra samosopryazhennykh differentsial'nykh uravneniy vtorogo poryadka [On Discrete Conditions for Spectrum of Self-adjoint Differential Equations of Second order] // Tr. MMO. – 1953. – V.2. – P. 169-200. [in Russian]
- Sobolev S.L. Ob otsenkakh nekotorykh summ dlya funktsiy, zadannykh na setke. [Estimates of Some Sums for Functions Defined on Grid] // Bul of AS of USSR. Math. Ser. – 1940. – № – P.5-17. [in Russian]
- Mustafina L.M. Raznostnyye teoremy vlozheniya prostranstv Soboleva s vesom [Difference Embedding Theorems for Sobolev Spaces with Weight] / Mustafina L.M., Bulabaev A.T. // All-Union School of Young Scientists: Tez. doc. – Tashkent. – 1988. – P. 121-122. [in Russian]
- Mynbaev K.T. Vesovyye funktsional'nyye prostranstva i spektr differentsial'nykh operatorov [Weighted Function Spaces and Spectrum of Differential Operators] / Mynbaev K.T., Otelbaev M. // M.: Nauka, 1988. [in Russian]
- Mukhamediev G.Kh. Plotnost' finitnykh funktsiy i teoremy vlozheniya dlya odnogo klassa vesovykh prostranstv [Density of Finite Functions and Embedding Theorems for Class of Weighted Spaces. // PhD thesis in Phys. and Math: Baku. 1986. [in Russian]