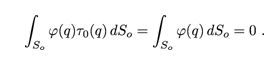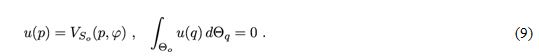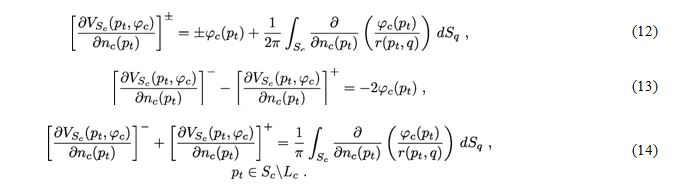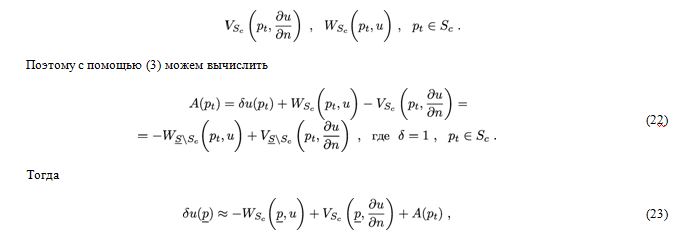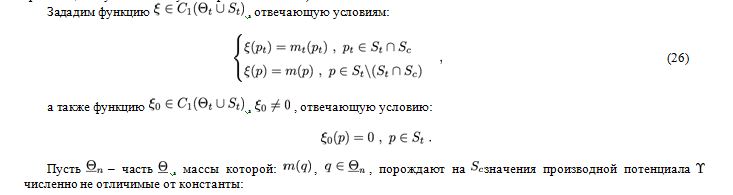ПРИМЕНЕНИЕ МЕТОДА ПОТЕНЦИАЛА В ГРАВИМЕТРИЧЕСКОЙ РАЗВЕДКЕ
ПРИМЕНЕНИЕ МЕТОДА ПОТЕНЦИАЛА В ГРАВИМЕТРИЧЕСКОЙ РАЗВЕДКЕ
Научная статья
ORCID: 0000-0001-9863-2484,
Российский университет транспорта, Москва, Россия
* Корреспондирующий автор (trubaevn[at]umail.ru)
АннотацияОпределение масс составляющих Землю компонентов по гравиметрическим измерениям важно для поиска полезных ископаемых и построения геоида. Наибольший интерес представляют величины масс в приповерхностном слое в несколько километров. В статье приводится численный способ определения величин этих масс в пространстве дифференцируемых функций, используя математический метод потенциала. В отличие от большинства известных алгоритмов способ приводит к решению корректно поставленной задачи, имеющей единственное решение. Описанный алгоритм обобщает предложенный ранее способ определения масс составляющих Землю компонентов в пространстве дифференцируемых функций с глобального на региональный уровень. По результатам глобального расчета можно получить исходные данные для вычисления уточненных значений масс составляющих Землю компонентов в приповерхностном слое, глубина которого определяется площадью полевых измерений. Увеличение площади полевых измерений позволяет использовать предлагаемую аппроксимацию на большей глубине и определить с заданной точностью величины масс.
Ключевые слова: теория потенциала, гравиметрия, геоид.
APPLICATION OF THE POTENTIAL METHOD IN GRAVIMETRIC EXPLORATION
Research article
Trubaev N.A.*
ORCID: 0000-0001-9863-2484,
Russian University of Transport, Moscow, Russia
* Corresponding author (trubaevn[at]umail.ru)
Abstract
Determination of the mass of the components of the Earth by gravimetric measurements is important for the search for minerals and the modelling of a geoid. Of the most interest is the magnitude of the masses in the near-surface layer of several kilometers. The article presents a numerical method for determining the values of these masses in a space of differentiable functions using the mathematical method of potential. Unlike most of the known algorithms, the method leads to the solution of a correctly posed problem with a single solution. The described algorithm generalizes the previously proposed method for determining the masses of the components of the Earth in the space of differentiable functions from the global to the regional level. Based on the results of the global calculation, it is possible to obtain initial data for calculating the refined values of the masses of the components composing the Earth in the near-surface layer, the depth of which is determined by the area of field measurements. The increase in the area of field measurements makes it possible to use the proposed approximation at a greater depth and determine the mass values with a given accuracy.
Keywords: potential theory, gravimetry, geoid.
Введение
Ознакомиться с историей и современным состоянием вопроса можно в [1], [4], [20], [3]. Автор уже обращался к заявленной теме. В [22] предложен алгоритм построения гравитационной модели Земли и геоида. В статье описана его адаптация с глобального на региональный уровень.
Используя предельные свойства ньютоновского потенциала простого слоя (1) и ньютоновского потенциала двойного слоя (2):
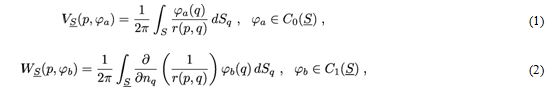 можно получить равенства (3) для гармонической в односвязной области функции [22], [6].
можно получить равенства (3) для гармонической в односвязной области функции [22], [6].
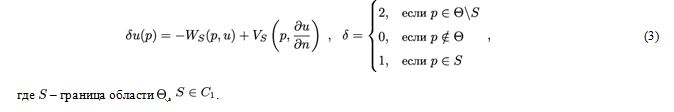
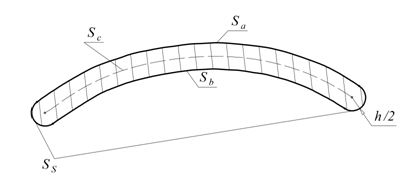
Предельные выражения для области ![]()
Рис. 1 – Одно из сечений области ![]()
Рассмотрим решения задач Дирихле для областей ![]() и R3\
и R3\![]() в виде потенциала простого слоя (1):
в виде потенциала простого слоя (1):
Ниже мы используем предельные выражения нормальной производной на границе гармонических функций S0, представленных потенциалами (4), (5). Значения гармонической функции в области R3\![]() по граничным значениям ее нормальной производной (внешняя задача Неймана) определяются единственным образом; так как потенциал (5) удовлетворяет условию излучения, то по граничным значениям S0 на его нормальной производной можно определить сам потенциал.
по граничным значениям ее нормальной производной (внешняя задача Неймана) определяются единственным образом; так как потенциал (5) удовлетворяет условию излучения, то по граничным значениям S0 на его нормальной производной можно определить сам потенциал.
Значения гармонической функции по граничным значениям ее нормальной производной в области ![]() (внутренняя задача Неймана) определяются с точностью до константы, уравнение [22], (12) индекс «+» , имеет решение при нулевой правой части. Для него справедливо
(внутренняя задача Неймана) определяются с точностью до константы, уравнение [22], (12) индекс «+» , имеет решение при нулевой правой части. Для него справедливо
Производная от (6) равна нулю, константа «исчезает»при дифференцировании.
В общем случае вид функции to не известен. В [18] показано, что в частном случае геометрии ![]() (рис. 1) функция toравна константе, то есть
(рис. 1) функция toравна константе, то есть
где co, c1 – константы.
Чтобы значения потенциалаИз условия (8) следует, что представляемая потенциалом ![]() гармоническая в
гармоническая в ![]() функция u ортогональна константе (7):
функция u ортогональна константе (7):
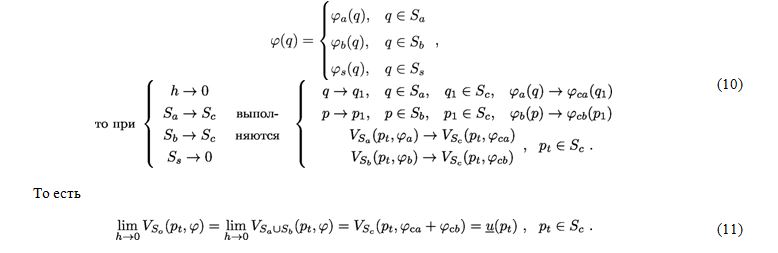 Если условие (8) не выполнено, предел (11) не существует [18].
Если условие (8) не выполнено, предел (11) не существует [18].
Ниже доказано, что при выполнении условия (9), равносильного условию (8), предел (11) существует.
Для потенциалаРассмотрим предельное изнутри ![]() значение на So нормальной производной от (4) в точке
значение на So нормальной производной от (4) в точке ![]() с учетом [22], (12) индекс «+», (10):
с учетом [22], (12) индекс «+», (10):
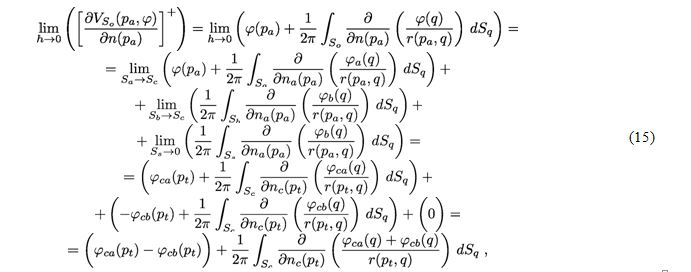 где точка pt – точка Sc, к которой стремится точка
где точка pt – точка Sc, к которой стремится точка 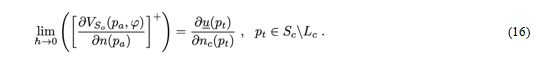 Так как правая часть (16) конечна по постановке задачи, то левая часть также конечна, следовательно пределы в (15) существуют, плотности
Так как правая часть (16) конечна по постановке задачи, то левая часть также конечна, следовательно пределы в (15) существуют, плотности В частном случае, когда Sc – часть плоскости, второе слагаемое в последнем равенстве (15) равно нулю, следовательно, имея ввиду (12), где второе слагаемое правой части также равно нулю, существует потенциал
где Sc – часть плоскости.
Из (9), (7) следует, что в (20) нормальная производная удовлетворяет условию:
 С помощью (20) по значениям нормальной производной на поверхности Sc можно определить значения гармонической функции на поверхности Sc. Построим численную процедуру определения приближенных значений гармонической функции u вблизи поверхности Sc по ее значениям и значениям ее нормальной производной на поверхности Sc на основе равенства (3) и оценим степень приближения.Аппроксимация на основе равенств (3)
С помощью (20) по значениям нормальной производной на поверхности Sc можно определить значения гармонической функции на поверхности Sc. Построим численную процедуру определения приближенных значений гармонической функции u вблизи поверхности Sc по ее значениям и значениям ее нормальной производной на поверхности Sc на основе равенства (3) и оценим степень приближения.Аппроксимация на основе равенств (3)
Пусть поверхность Sc является частью гладкой границы S односвязной области Q, включающей в себя Землю, 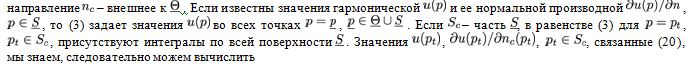
Поэтому с помощью (3) можем вычислить
где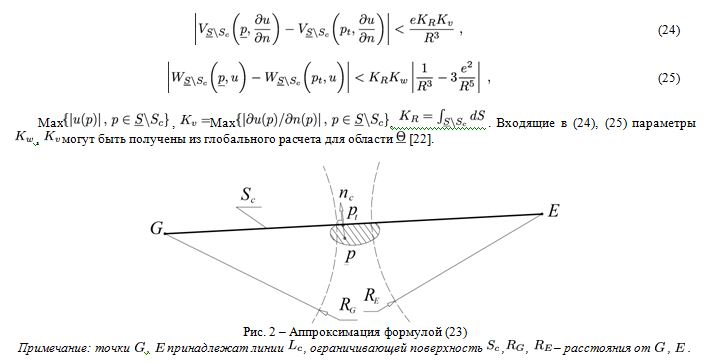 Следовательно,
Следовательно, Решение обратной задачи
Если мы имеем результаты глобального расчета [22] для области
 где индекс «+» соответствует стремлению из , индекс «–» – стремлению из . Действительно, по причине аналогичной описанной в [22] решение должно удовлетворять условию [22, (36)]:
где индекс «+» соответствует стремлению из , индекс «–» – стремлению из . Действительно, по причине аналогичной описанной в [22] решение должно удовлетворять условию [22, (36)]:

Заключение
Описанный в статье алгоритм позволяет обобщить предложенный в [22] способ определения масс составляющих Землю компонентов в пространстве дифференцируемых функций с глобального на региональный уровень. По результатам глобального расчета [22] с помощью предельного соотношения (20) и аппроксимации (23) можно получить исходные данные для решения уравнения [22], (33), что позволяет вычислить уточненные значения масс составляющих Землю компонентов (35) в приповерхностном слое, глубина которого определяется площадью полевых измерений. Увеличение площади полевых измерений позволяет использовать аппроксимацию (23) на большей глубине и определить с заданной точностью величины масс. Точность расчета известна до его проведения. Решение уравнения [22], (33) является корректно поставленной задачей, имеющей единственное решение. Корректность постановки математической задачи является преимуществом предлагаемого алгоритма по сравнению с большинством известных. Результаты расчета можно использовать при поиске полезных ископаемых и уточнении параметров геоида.
Не претендуя на полноту обзора, рассмотрим сравнение предлагаемого алгоритма с некоторыми реализованными подходами оценки гравиметрических данных [7], [3], [19], [14].
Основным преимуществом предлагаемого алгоритма является сведение решения к корректно поставленной задаче, имеющей единственное решение, «центральная вычислительная задача гравиметрии» [15] решена. Нет необходимости проводить регуляризацию, устойчивость решения к ошибкам округления в процессе численного счета «обеспечивается»наличием первого слагаемого в [22, (33)]. То есть, не рассматривается интегральное уравнение Фредгольма первого рода, являющееся некорректно поставленной задачей, решение сводится к рассмотрению интегрального уравнения Фредгольма второго рода – корректно поставленной задаче. Поэтому единственное решение может быть получено устойчиво к ошибкам округления. Проводить «фильтрацию помех правой части» [3], [16], [17] нет необходимости. При этом Земля численно рассматривается как объемное трехмерное тело с гладкой поверхностью [22], «сведение» к какому-либо телу вращения не производится. При переходе на региональный уровень используется аппроксимация (23), глубина применения которой ограничивается только точностью измерительной аппаратуры, если плоскую поверхность продолжить от заштрихованной области (рис. 2) далеко от поверхности Земли, используя данные спутниковой гравиметрии. Нет необходимости априорных оценок [7], [2], [19], [14], рассматривается единственное в пределах Земли решение, точность которого определяется полнотой натурных измерений и известна до проведения расчета.
Это единственное в пределах Земли решение обратной задачи гравиметрии при представлении величин масс составляющих Землю компонентов дифференцируемой функцией можно постоянно уточнять, используя полевые измерения величин этой функции на поверхности Земли и поверхностных и надповерхностных измерений силы тяжести, в чем заключается основная новизна и практическая ценность предлагаемого алгоритма.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Алексидзе М.А. Приближенные методы решения прямых и обратных задач гравиметрии / М. А. Алексидзе. – М.: Наука, 1987. – 336 с.
- Балк П.И. Аддитивные технологии количественной интерпретации гравитационных аномалий. /П. И. Балк, А. С. Долгаль // Геофизика. – 2016. – № 1. – С. 43-47.
- Блох Ю.И. Интерпретация магнитных и гравитационных аномалий / Ю. И. Блох. - 2009. –[Электронный ресурс].URL:http://sigma3d.com/index.php/en/publications/books(дата обращения: 12.11.2021)
- Бровар B.В. Гравиметрия и геодезия / B. В. Бровар. – М.: Научный мир, 2010. – 560 c.
- Бычков С.Г. Объемное моделирование геологических объектов по гравитационному полю на основе синтеза качественных и количественных методов интерпритации. / С. Г. Бычков, А. С. Долгаль, В. И. Костицыни др. // Геофизика. – 2015. – № 5. – С. 47-54.
- Гюнтер Н.М. Теория потенциала и ее применение к основным задачам математической физики /Н. М.Гюнтер. – М.: Гос. изд-во технико-теоретической литературы, 1953. – 416 c.
- Долгаль А.С. Размышления о структуре нового учебника по курсу “Гравиразведка” для студентов ВУЗов. / А. С. Долгаль, В. И. Костицын // Геофизика. – 2014. – № 5. – С. 88-93.
- Заварзина Г.А. Результаты комплексного анализа аэрогравимагнитных и сейсморазведочных данных восточной части Восточно-Сибирского моря. / Г. А. Заварзина, Р. Р. Мурзин, О. А. Захароваи др.// Геофизика. – 2017. – № 4. – С. 69-75.
- Каленицкий А.И. Еще раз о редукционных проблемах гравиметрии / А. И. Каленицкий// Интерэкспо Гео-Сибирь. – 2006. – Т. 3. – № 2. – C. 130-143.
- Кащеев Р.А. Современные методы спутниковой гравиметрии /Р. А. Кащеев. – Казань: Казанский университет, 2015. – 45 c.
- Кочнев В.А. Технология расчета плотностной и скоростной моделей и статических поправок по гравиметрическим данным. / В. А. Кочнев, И. В. Гоз, В. С. Поляков // Геофизика. – 2014. – № 1. – С. 2-7.
- Михайлов А.А. Курс гравиметрии и теории фигуры Земли. – М.: РЕДБЮРО ГУГК при СНК СССР, 1939. – 432 с.
- Молоденский М.С. Гравитационное поле, фигура и внутреннее строение Земли / М. С. Молоденский. – М.: Наука, 2001. – 569 c.
- Петрищевский А.М. Одно практическое следствие теорем единственности и эквивалентности обратных задач гравитационного потенциала. / А. М. Петрищевский // Геофизика. – 2020. – № 4. – С. 98-111.
- Страхов В.Н. О центральной вычислительной задаче гравиметрии, магнитометрии, геодезии и геоинформатики. / В. Н. Страхов // Физика Земли. – 2008. – № 2. – С. 63-79.
- Страхов В.Н. Как следует решать системы линейных алгебраических уравнений с симметрическими положительно полуопределенными матрицами, возникающие в задачах гравиметрии и магнитометрии. / В. Н. Страхов // Физика Земли. – 2012. – № 9-10. – С. 13-16.
- Страхов В.Н. Будущее теории интерпритации гравитационных аномалий. / В. Н. Страхов // Физика Земли. – 2013. – № 6. – С. 151-168.
- Трубаев Н.А. Применения теории ньютоновского потенциала / Трубаев Н. А. // Материалы XXIX Международной научно-практической конференции “Инновационные исследования как локомотив развития современной науки: от теоретических парадигм к практике”. 20 октября 2020 г., Москва: НИЦ МИСИ. – С.163-185.
- Чадаев М.С. Гравиметрическое изучение зоны арктического шельфа и континента. / М. С. Чадаев, В. И. Костицын, Р. Г. Ибламинов идр. // Геофизика. – 2017. – № 5. – С. 17-24.
- Sjoberg L. E. Gravity inversion and integration. Theory and applications in geodesy and geophysics / L. E. Sjoberg, M. Bagherbandi. – New York: Springer, 2017. – 391 p.
- Strakhov V. N. Change of epochs in Earth sciences / V. N. Strakhov // Russian journal of Earth sciences. – 2007. – Vol. 9. – No 1. – P. ES1001-19. DOI:10.2205/2007ES000217
- Trubaev N. А. The numerical solving of one inverse problem of the theory of the Newtonian potential / N. А. Trubaev// Modern Science. – 2021. № 1-1, pp.335-344.
Список литературы на английском языке / References in English
- Aleksidze M. A. Priblizhennye metody resheniia priamykh i obratnykh zadach gravimetrii [Approximate methods for solving direct and inverse problems of gravimetry] / M. A. Aleksidze. – Moscow: Nauka, 1987. – 336 p. [in Russian]
- Balk P. I. Additivnye tekhnologii kolichestvennoi interpretatsiigravitatsionnykh anomalii [The additive technologies of quantitative interpretation of the gravitational anomalies] / P. I. Balk, A. S. Dolgal' // Geofizika. – 2016. – №1. – P. 43-47. [in Russian]
- Blokh Yu.I. Interpretatsiya magnitnykh i gravitatsionnykh anomalii [The interpretation of the magnetic and gravitational anomalies] / Yu.I. Blokh. - 2009. – [Electronic resource].URL: http://sigma3d.com/index.php/en/publications/books (accessed: 12.11.2021) [in Russian]
- Brovar B. V. Gravimetriia i geodeziia [Gravimetry and geodesy] / B. V. Brovar.– Moscow: Nauchnyi mir, 2010. – 560 p. [in Russian]
- Bychkov S. G. Ob"emnoe modelirovanie geologicheskikh ob"ektov po gravitatsionnomu polyu na osnove sinteza kachestvennykh i kolichestvennykh metodov interpritatsii [3D modeling of geological objects based on the synthesis of qualitative and quantitative interpretation methods of the gravitational field] / S. G. Bychkov, A. S. Dolgal', V. I. Kostitsyn et al. // Geofizika. – 2015. – №5. – P. 47-54. [in Russian]
- Gyunter N. M. Teoriya potentsiala i ee primenenie k osnovnym zadacham matematicheskoi fiziki [Potential theory and its application for basic problems of mathematical physics] / N. M. Gyunter. – Moscow: StatePublishing house of tekh and theoretical literature, 1953. – 416 p. [in Russian]
- Dolgal' A. S. Razmyshleniya o strukture novogo uchebnika po kursu “Gravirazvedka” dlya studentov VUZov [Some ideas of the structure of the new textbook for the course "Gravimetric prospecting" for university students] / A. S. Dolgal', V. I. Kostitsyn // Geofizika. – 2014. – №5. – P. 88-93. [in Russian]
- Zavarzina G. A. Rezul'taty kompleksnogo analiza aerogravimagnitnykh i seismorazvedochnykh dannykh vostochnoi chasti Vostochno-Sibirskogo moray [The results of the complex analysis of the aerogravimagnetic and seismic researches of the eastern part of East-Siberian sea] / G. A. Zavarzina, R.R. Murzin, O. A. Zakharova et al. // Geofizika. – 2017. – №4. – P. 69-75. [in Russian]
- Kalenitskii A. I. Eshche raz o reduktsionnykh problemakh gravimetrii [Once again about the reduction problems of gravimetry] / A. I.Kalenitskii // Interekspo Geo-Sibir’. – 2006. № 3, 4, – Р. 130-143 [in Russian]
- Kashcheev R. A. Sovremennye metody sputnikovoi gravimetrii [The modern methods of satellite gravimetry] / R. A. Kashcheev. – Kazan: Kazanskii universitet, 2015. – 45 p. [in Russian]
- Kochnev V. A. Tekhnologiya rascheta plotnostnoi i skorostnoi modeleii staticheskikh popravok po gravimetricheskim dannym [The technology of calculation of the density and velocity models and static corrections of the gravimetric data] / V. A. Kochnev, I. V. Goz, V. S. Polyakov // Geofizika. – 2014. – №1. – P. 2-7. [in Russian]
- Mikhailov A.A. Kurs gravimetrii i teorii figury Zemli [Theoretical course of gravimetry and Earth shape]. – Moscow: REDBYuRO GUGK pri SNK SSSR, 1939. – 432 p. [in Russian]
- Molodenskii M. S. Gravitatsionnoe pole, figura i vnutrennee stroenie Zemli [Gravitational field, figure and internal structure of the Earth] / M. S.Molodenskii. – Moscow: Nauka, 2001. – 569 p. [in Russian]
- Petrishchevskii A. M. Odno prakticheskoe sledstvie teorem edinstvennosti i ekvivalentnosti obratnykh zadach gravitatsionnogo potentsiala [One practical consequence of the uniqueness and equivalence theorems of the inverse problems of gravitational potential] / A. M. Petrishchevskii // Geofizika. – 2020. – №4. – P. 98-111. [in Russian]
- Strakhov V. N. O tsentral'noi vychislitel'noi zadache gravimetrii, magnitometrii, geodezii i geoinformatiki [The central computational problem of gravimetry, magnetometry, geodesy and geoinformation system] / V. N. Strakhov // Fizika Zemli. – 2008. – №2. – P. 63-79. [in Russian]
- Strakhov V. N. Kak sleduet reshat' sistemy lineinykh algebraicheskikh uravnenii s simmetricheskimi polozhitel'no poluopredelennymi matritsami, voznikayushchie v zadachakh gravimetrii i magnitometrii [The way of solving of the systems of linear algebraic equations with symmetric positive semidefinite matrices in the problems of gravimetry and magnetometry] / V. N. Strakhov // Fizika Zemli. – 2012. – №9-10. – P. 13-16. [in Russian]
- Strakhov V. N. Budushchee teorii interpritatsii gravitatsionnykh anomalii [The future of the theory of interpretation of the gravitational anomalies] / V. N. Strakhov // Fizika Zemli. – 2013. – №6. – P. 151-168. [in Russian]
- Trubaev N. А. The applications of the theory of the Newtonian potential / Trubaev N. А. // Materialy XXIX Mezhdunarodnoi nauchno-prakticheskoi konferentsii “Innovatsionnye issledovaniya kak lokomotiv razvitiya sovremennoi nauki: ot teoreticheskikh paradigm k praktike”. 20 oktyabrya 2020 g., – Moscow: NITs MISI, 2020. – pp. 163-185.
- Chadaev M. S. Gravimetricheskoe izuchenie zony arkticheskogo shel'fa i kontinenta [The gravimetric analysis of the Arctic shelf zone and the continent] / M. S. Chadaev, V. I. Kostitsyn, R. G. Iblaminov et al. // Geofizika. – 2017. – №5. – P. 17-24. [in Russian]
- Sjoberg L. E. Gravity inversion and integration. Theory and applications in geodesy and geophysics / L. E. Sjoberg,M. Bagherbandi. – New York: Springer, 2017. – 391 p.
- Strakhov V. N. Change of epochs in Earth sciences / V. N. Strakhov // Russian journal of Earth sciences. – 2007. – Vol. 9. – No 1. – P. ES1001-19. DOI:10.2205/2007ES000217
- Trubaev N. А. The numerical solving of one inverse problem of the theory of the Newtonian potential / N. А. Trubaev // Modern Science. – 2021. № 1-1, – Р.335-344.