ПРИМЕНЕНИЕ ФУНКЦИЙ VBA EXCEL В АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
ПРИМЕНЕНИЕ ФУНКЦИЙ VBA EXCEL В АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
Научная статья
Российский государственный университет туризма и сервиса, Пушкино, Россия
* Корреспондирующий автор (oasdv[at]yandex.ru)
АннотацияПриведены программные коды двух пользовательских функций VBA Excel. Первая из них находит или координаты точки пересечения двух прямых плоскости, или тангенс угла между ними, или угловой коэффициент прямой, по которой луч света, движущийся по первой прямой, движется после отражения от второй прямой. Вторая функция находит или величину расстояния между скрещивающимися прямыми, или координаты точки, через которую проходит общий перпендикуляр скрещивающихся прямых, или направляющий вектор их общего перпендикуляра, или параметрические уравнения их общего перпендикуляра, или величину расстояния от заданной точки первой прямой до второй прямой. Все вычисления проводятся онлайн и не требуют данных рабочих листов Excel. Применение разработанных пользовательских функций показано на конкретных задачах.
Ключевые слова: луч света, скрещивающиеся прямые, общий перпендикуляр, код, диалоговое окно.
USING VBA EXCEL FUNCTIONS IN ANALYTICAL GEOMETRY
Research article
Sdvizhkov O.A.*
Russian State University of Tourism and Service, Pushkino, Russia
* Corresponding author (oasdv[at]yandex.ru)
AbstractThe article contains the software codes of two VBA Excel custom functions. The first function finds either the coordinates of the point of intersection of two straight planes, or the tangent of the angle between them, or the slope of the straight line, in which a ray of light, while moving along the first straight line, moves after the reflection from the second line. The second function finds either the distance between intersecting lines, or the coordinates of the point, through which passes the common perpendicular of the intersecting lines, or the guiding vector of their common perpendicular, or the parametric equations of their common perpendicular, or the distance from a given point of the first straight line to the second straight line. All calculations are performed online and do not require Excel worksheet data. The application of the developed custom functions is demonstrated through specific tasks.
Keywords: light beam, intersecting straight lines, common perpendicular, code, dialog box.
ВведениеВ статье «Аналитическая геометрия (пользовательские функции)» [10] приведены программные коды около 15 пользовательских функций VBA Excel, предназначенных для решения задач аналитической геометрии [1], [5], [6] в режиме онлайн. Две из них рассматриваются в данной статье. Следует заметить, что в связи с переходом к информационному обществу, в котором все задачи должны решаться на компьютере, причем в режиме онлайн, задача информатизации вычислений, в том числе и по аналитической геометрии, является одной из наиболее актуальных задач. Рассматриваемые в статье задачи специальных инструментов решений в математических пакетах [4], [8], [9] не имеют.
Применяемый для решения рассматриваемых задач программный комплекс Excel – один из самых популярных и доступных программных комплексов, предназначенный для обработки числовых данных, причем заложенная в Excel среда программирования VBA позволяет пользователю создавать собственные процедуры, автоматизирующие математические вычисления [2], [3], [7].
В основном в VBA Excel разрабатываются проекты [2], [3], [7], то есть процедуры Sub. В данной статье применяется более простая, но достаточно эффективная процедура Function, которой создаются пользовательские функции VBA, имеющие встроенные диалоговые окна ввода данных, что позволяет не тратить время на создание пользовательских форм.
Основной особенностью рассматриваемых в статье пользовательских функций является то, что они позволяют, используя конструкцию Select Case, находить значения нескольких параметров, что существенно уменьшает необходимое число пользовательских функций. Последней переменной каждой функции является строковая переменная, показывающая значение какого параметра требуется вычислить.
Пользовательская функция ОТРАЖЕНИЕ
Пусть уравнениями А1х+В1у+С1=0 и А2х+В2у+С2=0 заданы две прямые и надо найти уравнение прямой, по которой луч света, движущийся по первой прямой, будет двигаться после отражения от второй прямой. Программный код пользовательской функции ОТРАЖЕНИЕ, позволяющий решить онлайн эту задачу на компьютере, приведен в листинге 1.1.
Листинг 1.1. Код функции ОТРАЖЕНИЕ и ее описания
Function ОТРАЖЕНИЕ(Прямая1() As Variant, Прямая2() _
As Variant, I_T_L As String)
Dim A(1 To 2) As Single, B(1 To 2) As Single, C(1 To 2) _
As Single, M(1 To 2) As Variant
A(1) = Прямая1(1): B(1) = Прямая1(2): C(1) = Прямая1(3)
A(2) = Прямая2(1): B(2) = Прямая2(2): C(2) = Прямая2(3)
D = A(1) * B(2) - A(2) * B(1)
D1 = B(1) * C(2) - B(2) * C(1)
D2 = C(1) * A(2) - C(2) * A(1)
T = D / (A(1) * A(2) + B(1) * B(2))
Select Case I_T_L
Case "I":M(1) = D1 / D:M(2) = D2 / D
ОТРАЖЕНИЕ = M
Case "T"
ОТРАЖЕНИЕ = T
Case "L"
ОТРАЖЕНИЕ = (T * B(2) - A(2)) / (B(2) + T * A(2))
End Select
End Function
Sub InstallFunc1()
Application.MacroOptions Macro:="ОТРАЖЕНИЕ", Description:= _
"При I находит точку пересечения прямых, заданных " & _
"коэф. общ. ур. прямых, при T - тангенс угла между " & _
"прямыми, при L - угл. коэф. прямой, получаемой " & _
"отражением 1-й прямой от 2-й прямой"
End Sub
По листингу 1.1 стандартным образом [2], [3] создается функция ОТРАЖЕНИЕ.
Задача 1.1. Луч света направлен по прямой х-2у+5=0. Дойдя до прямой 3х-2у+7=0, луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч.
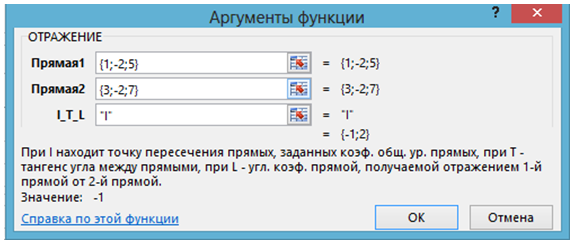
Технология решения. 1. Вызывается функция ОТРАЖЕНИЕ и находятся координаты точки пересечения прямых:
Рис. 1.1 – Первое применение функции ОТРАЖЕНИЕ в задаче 1.1
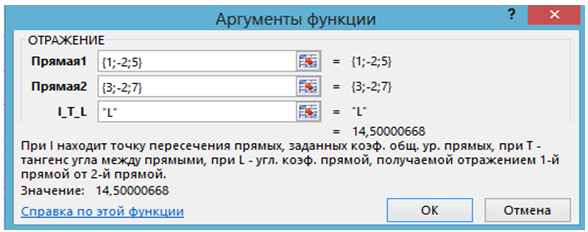
- Вызывается функция ОТРАЖЕНИЕ и находится угловой коэффициент прямой, на которой лежит отраженный луч:
Рис. 1.2 – Второе применение функции ОТРАЖЕНИЕ в задаче 1.1
Остается выписать ответ: у-2=14,5(х+1).
Если надо найти тангенс угла между заданными прямыми, то применяется функция ОТРАЖЕНИЕ, когда значение последнего параметра “T”:
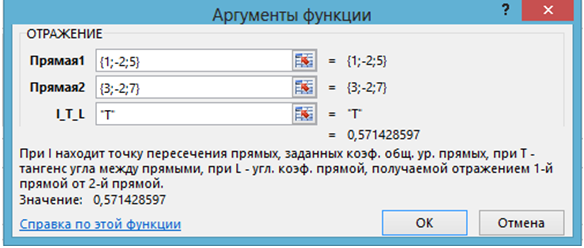
Рис. 1.3 – Нахождение тангенса угла между прямыми
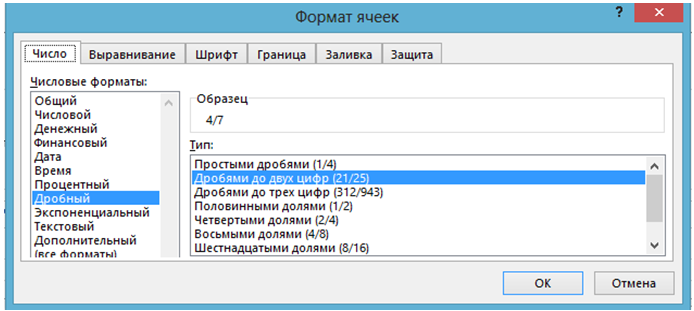
Переход к дробному формату дает:Рис. 1.4 – Диалоговое окно «Формат ячеек»
Задача 1.2. Из точки М(5, 4) выходит луч света под углом φ = arctg 2 к оси Ох и отражается от нее. Написать уравнение отраженного луча.
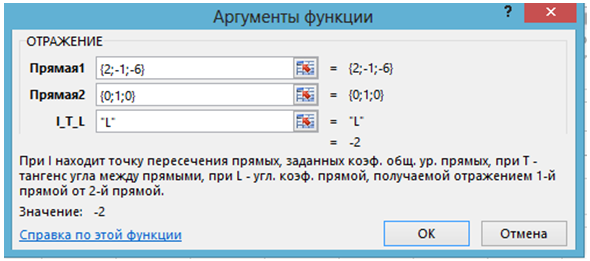
Технология решения. Уравнение падающего луча у-4=2(х-5), подстановка у=0 дает х=3. Вызывается функция ОТРАЖЕНИЕ и вводятся данные:
Рис. 1.5 – Применение функции ОТРАЖЕНИЕ в задаче 1.2
Следовательно, уравнение отраженного луча у=-2(х-3).Пользовательская функция СКРЕЩ
Пусть прямая a задана точкой ![]() и направляющим вектором
и направляющим вектором ![]() , а прямая b задана точкой
, а прямая b задана точкой ![]() и направляющим вектором
и направляющим вектором ![]() , причем векторы
, причем векторы ![]() – линейно независимые, то есть прямые a и b являются скрещивающимися. Тогда расстояние d между ними вычисляется [5,С. 39] по формуле:
– линейно независимые, то есть прямые a и b являются скрещивающимися. Тогда расстояние d между ними вычисляется [5,С. 39] по формуле:
Направляющим вектором общего перпендикуляра прямых a и b является вектор ![]() . Общий перпендикуляр является пересечением плоскостей, первая из которых определяется точкой М и векторами
. Общий перпендикуляр является пересечением плоскостей, первая из которых определяется точкой М и векторами ![]() , а вторая точкой Р и векторами
, а вторая точкой Р и векторами ![]() .
.
Расстояние h от точки М до прямой, заданной точкой Р и вектором ![]() , находится [1, С. 67] по формуле:
, находится [1, С. 67] по формуле:
Программный код функции СКРЕЩ, возвращающей или величину расстояния между скрещивающимися прямыми, или координаты точки, через которую проходит общий перпендикуляр скрещивающихся прямых, или направляющий вектор их общего перпендикуляра, или параметрические уравнения их общего перпендикуляра, или расстояние от точки 1 до второй прямой, имеет вид, приведенный в листинге 2.1.
Листинг 2.1. Код функции СКРЕЩ и ее описания
Function СКРЕЩ(Точка1() As Variant, Вектор1() As Variant, _
Точка2() As Variant, Вектор2() As Variant, D_P_C_L_H _
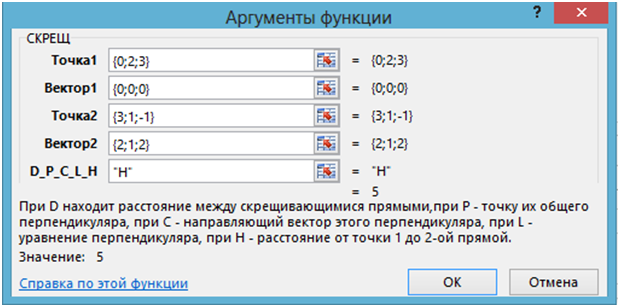
As String) Dim M(1 To 3) As Variant, a(1 To 3) As Variant Dim P(1 To 3) As Variant, b(1 To 3) As Variant Dim c(1 To 3) As Variant Dim r(1 To 3) As Variant Dim g(1 To 3) As Variant Dim Q(1 To 3) As Variant Dim X(1 To 3) As Variant For i = 1 To 3 M(i) = Точка1(i) a(i) = Вектор1(i) P(i) = Точка2(i) b(i) = Вектор2(i) Next If a(1) = a(2) = a(3) = 0 Then a(1) = 1 c(1) = a(2) * b(3) - a(3) * b(2) c(2) = a(3) * b(1) - a(1) * b(3) c(3) = a(1) * b(2) - a(2) * b(1) S = (c(1) ^ 2 + c(2) ^ 2 + c(3) ^ 2) ^ (1 / 2) r(1) = P(1) - M(1): r(2) = P(2) - M(2): r(3) = P(3) - M(3) g(1) = a(2) * c(3) - a(3) * c(2) g(2) = a(3) * c(1) - a(1) * c(3) g(3) = a(1) * c(2) - a(2) * c(1) h = M(1) * g(1) + M(2) * g(2) + M(3) * g(3) h = h - P(1) * g(1) - P(2) * g(2) - P(3) * g(3) t = h / (b(1) * g(1) + b(2) * g(2) + b(3) * g(3)) Q(1) = P(1) + b(1) * t Q(2) = P(2) + b(2) * t Q(3) = P(3) + b(3) * t For i = 1 To 3 c(i) = Round(c(i), 4) Q(i) = Round(Q(i), 4) Next Select Case D_P_C_L Case "D" СКРЕЩ = (c(1) * r(1) + c(2) * r(2) + c(3) * r(3)) / S СКРЕЩ = Abs(СКРЕЩ) Case "P":СКРЕЩ = Q Case "C":СКРЕЩ = c Case "L" For i = 1 To 3 If c(i) < 0 Then X(i) = Q(i) & "-" & -c(i) & "t" Else X(i) = Q(i) & "+" & c(i) & "t" End If Next СКРЕЩ = X Case "H" СКРЕЩ = ((r(2)*b(3)-r(3)*b(2))^2 + _ (r(1)*b(3)-r(3)*b(1))^2+ _ (r(1)*b(2)-r(2)*b(1))^2)^(1/2)/ _ (b(1)^2+b(2)^2+b(3)^2)^(1/2) СКРЕЩ=Round(СКРЕЩ,4) End Select End Function Sub InstallFunc2() Application.MacroOptions Macro:="СКРЕЩ", Description:= _ "При D находит расстояние между скрещивающимися прямыми," & _ "при Р - точку их общего перпендикуляра, при С - " & _ "направляющий вектор этого перпендикуляра, при L – " & _ "уравнение перпендикуляра, при H – расстояние от точки 1 " & _ "до 2-ой прямой" End Sub Задача 2.1. Заданы прямые: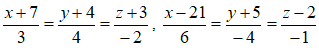 Применяя функцию СКРЕЩ, найти:
Применяя функцию СКРЕЩ, найти:
1) расстояние между прямыми;
2) координаты точки, через которую проходит их общий перпендикуляр;
3) координаты направляющего вектора их общего перпендикуляра;
4) параметрические уравнения их общего перпендикуляра.
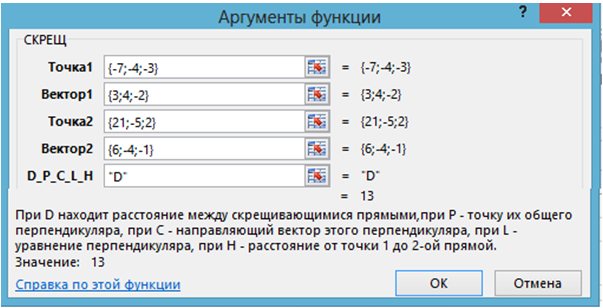
Технология решения. 1) Вызывается функция СКРЕЩ, вводятся данные задачи и “D”:
Рис. 2.1 – Применение функции СКРЕЩ в задаче 2.1.1
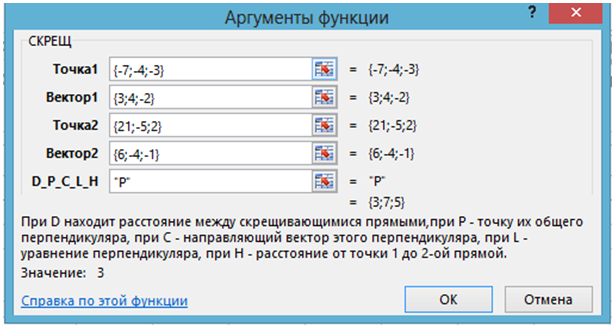
2) Вызывается функция СКРЕЩ, вводятся данные задачи и “P”:Рис. 2.2 – Применение функции СКРЕЩ в задаче 2.1.2
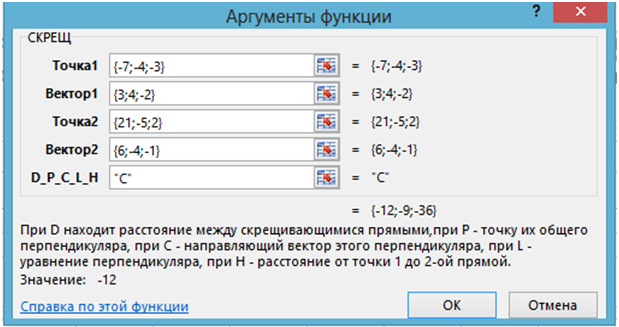
3) Вызывается функция СКРЕЩ, вводятся данные задачи и “C”:Рис. 2.3 – Применение функции СКРЕЩ в задаче 2.1.3
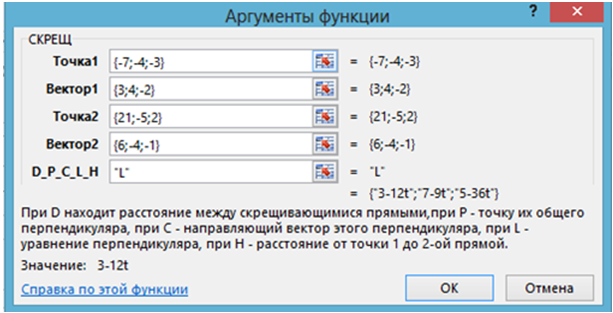
4) Вызывается функция СКРЕЩ, вводятся данные задачи и “L”:Рис. 2.4 – Применение функции СКРЕЩ в задаче 2.1.4
Задача 2.2. Применяя функцию СКРЕЩ, найдите расстояние от точки М(0, 2, 3) до прямой:Рис. 2.5 – Применение функции СКРЕЩ в задаче 2.2
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. / Д. В. Беклемишев – М.: «Наука», 1976. – 320с.
- Гарбер Г.З. Основы программирования на Visual Basic и VBA Excel 2007. / Г. З. Гарбер – М.: СОЛОН-ПРЕСС, 2008. – 192 с.
- Гарнаев А.Ю. MS Excel 2002: разработка приложений. / А. Ю. Гарнаев – СПб.: БХВ-Петербург, 2003. – 768 с.
- Дьяконов В.П. Mathematica 5/6/7. Полное руководство. / В. П. Дьяконов – М.: ДМК Пресс, 2010. 624 с.
- Ефимов А.В. Сборник задач по математике для втузов. В 4 частях. Ч. 1: Учебное пособие для втузов / Под общ. ред. А. В. Ефимова и А. С. Поспелова. – 4-е изд. перераб. и доп. – М.: Издательство Физико-математической литературы, 2003. – 288 с.
- Клетеник Д.В. Сборник задач по аналитической геометрии: Учебное пособие. 17-е изд., стер. / По ред. Н. В. Ефимова. – СПб.: Издательство «Лань», 2016. – 224 с.
- Сдвижков О.А. Excel-VBA. Словарь-справочник пользователя / О.А. Сдвижков – М.: Эксмо, 2008.
- Сдвижков О.А. MATHCAD-2000. / О.А. Сдвижков – М.: Издательско-торговая корпорация «Дашков и К°», 2002. – 204 с.
- Сдвижков О.А. Математика на компьютере: Maple 8. / О.А. Сдвижков – М.: СОЛОН-ПРЕСС, 2003. – 176 с.
- Сдвижков О.А. Аналитическая геометрия (пользовательские функции) [Электронный ресурс] – URL: https://oas.ucoz.com/load/analiticheskaja_geometrija_polzovatelskie_funkcii/1-1-0-31 (дата обращения: 14.10.2020)
Список литературы на английском языке / References in English
- Beklemishev D. V. Kurs analiticheskoi geometrii i lineinoi algebry [Course in Analytical Geometry and Linear Algebra] / D. V. Beklemishev — M.: "Nauka", 1976 – 320 p. [in Russian]
- Garber G. Z. Osnovy programmirovaniia na Visual Basic i VBA Excel 2007 [Basics of Programming in Visual Basic and VBA Excel 2007] / G. Z. Garber — M.: SOLON-PRESS, 2008. - 192 p. [in Russian]
- Garnaev A. Yu. MS Excel 2002: razrabotka prilozhenii [MS Excel 2002: Application Development] / A. Yu. Garnaev — SPb.: BHV-Peterburg, 2003. — 768 p. [in Russian]
- Diakonov V. P. Mathematica 5/6/7. Polnoe rukovodstvo [Mathematica 5/6/7. A Complete Guide.] / V. P. Diakonov — M.: DMK Press, 2010. 624 p. [in Russian]
- Efimov, A. V. Sbornik zadach po matematike dlia vuzov. V 4 chastiakh. Ch. 1: Uchebnoe posobie dlia vtuzov [Collection of Problems in Mathematics for Higher Education Institutions. In 4 Parts. Part 1: A Textbook for Higher Education Institutions] / A. V. Efimov et al. Edited by A. V. Efimov and A. S. Pospelova. – 4th Edition. Revised and Updated. M.: Publ. house of Fiz-math literature, 2003, 288 p. [in Russian]
- Kletenik D. V. Sbornik zadach po analiticheskoi geometrii: Uchebnoe posobie [Collection of Problems in Analytical Geometry: a Textbook] / D. V. Kletenik. Edited by N. N. Efimov. 17th Edition, print run. — SPb: Publ. house "Lan'", 2016. - 224 p. [in Russian]
- Sdvizhkov O. A. Excel-VBA Slovar'-spravochnik pol'zovatelia [Excel-VBA. A Reference Book] / O. A. Sdvizhkov — M.: Eksmo, 2008. [in Russian]
- Sdvizhkov O. A. MATHCAD-2000. / O. A. Sdvizhkov — M.: Publ. house «Dashkov i K°», 2002. - 204 p. [in Russian]
- Sdvizhkov O. A. Matematika na komp'iutere: Maple 8 [Mathematics on the computer: Maple 8]. / O. A. Sdvizhkov — M.: SOLON-PRESS, 2003. - 176 p. [in Russian]
- Sdvizhkov O. A. Analiticheskaia geometriia (pol'zovatel'skie funktsii) [Analytical geometry (user-defined functions)] [Electronic resource] — URL: https://oas.ucoz.com/load/analiticheskaja_geometrija_polzovatelskie_funkcii/1-1-0-31 (accessed: 14.10.2020) [in Russian]