ПОСТРОЕНИЕ РАЗМЕЧЕННЫХ МНОЖЕСТВ ПРИМЕНЕНИЕМ ГАРМОНИЧЕСКИХ ФУНКЦИЙ
DOI: https://doi.org/10.23670/IRJ.2018.75.9.005
ПОСТРОЕНИЕ РАЗМЕЧЕННЫХ МНОЖЕСТВ ПРИМЕНЕНИЕМ ГАРМОНИЧЕСКИХ ФУНКЦИЙ
Научная статья
Мурзабаева А.Б.*
ORCID: 0000-0003-0694-6633,
Ошский технологический университет, Ош, Кыргызстан
* Корреспондирующий автор (aytbu.murzabaeva[at]mail.ru)
Аннотация
В данной статье на основе ранних работ построены размеченные области применением гармонических функций. Даны определения и обозначения размеченных областей, рассмотрены конкретные случаи размеченных областей. А также введено понятие ориентированные размеченные области. Приведены примеры ориентированных, размеченных областей. В качестве примера применения размеченных областей рассматривается линейное сингулярно возмущенное обыкновенное дифференциальное уравнение первого порядка. Для исследования асимптотического поведения решения начальной задачи построена размеченная область. Доказана, существует часть размеченной области являющиеся областью притяжения решения вырожденного уравнения.
Ключевые слова: размеченная область, гармоническая функция, линии уровня, сеть кривых, точки ветвления, сингулярно возмущенное уравнение, асимптотика.
CONSTRUCTION OF LABELED MULTITUDES USING POTENTIAL FUNCTIONS
Research article
Murzabaeva A.B.*
ORCID: 0000-0003-0694-6633,
Osh Technological University, Osh, Kyrgyzstan
* Corresponding author (aytbu.murzabaeva[at]mail.ru)
Abstract
In this paper, based on earlier papers, we constructed a labeled area using potential functions. The definitions and designations of labeled areas are given, specific cases of labeled areas are considered. The paper also introduces the concept of oriented labeled areas. Examples of oriented labeled areas are given. We consider a linear singularly perturbed ordinary differential equation of the first order as an example of the application of labeled area. A labeled area is constructed to study the asymptotic behavior of the solution of the initial problem. It is proved that there is a part of the labeled area that is the area of the attraction of the solution of the degenerate equation.
Keywords: labeled area, potential function, level lines, network of curves, branching points, singularly perturbed equation, asymptotics.
Пусть ![]() односвязная область.
односвязная область.
Определение 1. Если Ω полностью покрывается некоторым множеством кривых {L(A)}, где A произвольная точка, принадлежащая области Ω, то область Ω назовём размеченным множеством кривых {L(A)} и обозначим Ω({L(A)}) .
Ниже будем рассматривать конкретные случаи множества {L(A)}.
Примеры
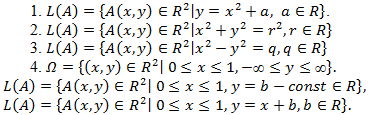
В [1] для исследования асимптотического поведения решений сингулярно возмущённых обыкновенных дифференциальных уравнений аналитическими функциями при нарушении условия устойчивости, точки покоя присоединенной системы введено понятие размеченное множество в множество комплексных чисел.
Определение 2. Если кривые L(A) из множества имеют определенную ориентацию (направление), то размеченное множество Ω назовём ориентированным и будем обозначать ![]() . Ориентация кривых зависит от некоторых параметров, значения которых определяют положение точки A.
. Ориентация кривых зависит от некоторых параметров, значения которых определяют положение точки A.
Области определенные в предыдущем примере являются ориентированными. Параметром ориентации служит независимая переменная x.
Займемся построением размеченных множеств, применением гармонических функций.
При построении размеченных областей используем частично результаты работ [1], [2], [3], [4], [5].
Пусть u(x,y)∈Γ(Ω) – пространство гармонических функций в области Ω.
Определение 3. Множество ![]() назовём линией уровня функции u(x,y) в области Ω.
назовём линией уровня функции u(x,y) в области Ω.
Предположим выполнения следующего условия
U.1. ![]()
Согласно условия U.1 линии уровня (L) не имеют кратных точек в области Ω, то есть через каждую точку области Ω проходит единственная линия уровня.
Таким образом область Ω является размеченной линиями уровней (L) функции u(x,y) и область Ω является размеченным.
Пример. ![]()
Линиями уровня функции u(x,y) являются концентрические окружности с центром в точке (0;0).
Пусть ![]() – пространство аналитических функций в области Ω.
– пространство аналитических функций в области Ω.
Полагая ![]() – действительные переменные, введем обозначения
– действительные переменные, введем обозначения ![]() ,
,
Функции ![]() являются сопряжено гармоническими в области Ω.
являются сопряжено гармоническими в области Ω.
Предположим выполнения условия
U.2. ![]()
Тогда функция F(z) в области Ω не имеет кратных точек, следовательно линии уровня функций ![]() также не имеют точек ветвления.
также не имеют точек ветвления.
Линии уровней ![]() являются взаимно ортогональными в точках пересечения. Таким образом область Ω полностью покрывается сетью взаимно ортогональных линии уровней функций
являются взаимно ортогональными в точках пересечения. Таким образом область Ω полностью покрывается сетью взаимно ортогональных линии уровней функций ![]() . В рассматриваемом случае область Ω размечена двумя видами множества кривых.
. В рассматриваемом случае область Ω размечена двумя видами множества кривых.
При нарушении условия U.2, в общем случае, представить размеченную область Ω, практически является трудной задачей и каждый из этих случаев, надо будет рассматривать отдельно. Такие случаи рассмотрены в [1], [3].
Теперь рассмотрим случай, когда заданы несколько аналитических функций в области Ω. Частично используем результаты работ [6-10].
U.3. Пусть ![]()
Введём обозначения
![]() ,
,
Согласно рассмотренному случаю линии уровня, определяемые парами ![]() полностью покрывают область Ω сетью взаимно ортогональных линии уровней и область Ω будет размеченным порознь парами
полностью покрывают область Ω сетью взаимно ортогональных линии уровней и область Ω будет размеченным порознь парами ![]() .
.
Размеченность области Ω парой ![]() обозначим
обозначим ![]() , а парой
, а парой ![]() обозначим
обозначим ![]() . Какова взаимосвязь размеченных областей
. Какова взаимосвязь размеченных областей ![]() ? Используя только условие U.3 решение поставленной задачи, практически является невозможным.
? Используя только условие U.3 решение поставленной задачи, практически является невозможным.
Пусть ![]() и является её внутренней точкой и U.4.
и является её внутренней точкой и U.4. ![]()
Возьмём ![]() Согласно U.4 имеем
Согласно U.4 имеем ![]() , следовательно, существует линия уровня
, следовательно, существует линия уровня ![]() которая проходит через точку
которая проходит через точку ![]() и область Ω делит на две части, которые обозначим
и область Ω делит на две части, которые обозначим ![]() .
.
По линиям уровней функции ![]() строго монотонна. Пусть
строго монотонна. Пусть ![]() произвольная точка, принадлежащая
произвольная точка, принадлежащая ![]() . Существует линия уровня
. Существует линия уровня ![]()
Рассмотрим ![]() . Так как
. Так как ![]() то в каждом из областей
то в каждом из областей ![]() принимает значения разных знаков.
принимает значения разных знаков.
Для определённости возьмём ![]() .
.
Тогда ![]() , причём равенство имеет место только для точек принадлежащих линии
, причём равенство имеет место только для точек принадлежащих линии ![]() .
.
Области ![]() являются размеченными и в совокупности определяют размеченную область
являются размеченными и в совокупности определяют размеченную область ![]() . Аналогично рассматривая функции
. Аналогично рассматривая функции ![]() определяем области
определяем области ![]() принимает значения разных знаков. Области
принимает значения разных знаков. Области ![]() имеют общую границу
имеют общую границу ![]() являются размеченными и в совокупности определяют размеченную область Ω.
являются размеченными и в совокупности определяют размеченную область Ω.
Для определённости считаем
![]() .
.
U.5. Пусть линии уровня ![]() и пересекаются только в точке
и пересекаются только в точке ![]() .
.
При выполнении условия U.5 существуют области, где функции ![]() принимают значения одинаковых или разных знаков, причём все области являются размеченными по линиям уровней функций
принимают значения одинаковых или разных знаков, причём все области являются размеченными по линиям уровней функций ![]()
Применение размеченных множеств для определения областей притяжения.
Размеченные множества применяются при исследовании асимптотического поведения решений сингулярно возмущённых уравнений и для определения областей притяжения решений вырожденных уравнений.
Более подробно применением размеченных множеств для различных классов сингулярно возмущённых уравнений можно ознакомиться в [1-10]. Для простоты рассмотрим линейное сингулярно возмущённое уравнение следующего вида
![]() (1)
(1)
с начальным условием
![]() (2)
(2)
где ![]() малый параметр;
малый параметр; ![]() - односвязная область;
- односвязная область; ![]() является её внутренней точкой.
является её внутренней точкой.
Пусть выполняются условия
![]()
Задача. Исследовать асимптотическое поведение решения задачи (1)-(2).
Для решения поставленной задачи решение задачи (1)-(2) представим в виде
![]() , (3)
, (3)
где ![]() .
.
Выполняются все условия раздела II. Область Ω полностью покрывается сетью взаимно ортогональных линии уровней функций ![]() является размеченным.
является размеченным.
Функцию (3) будем рассматривать в размеченной области Ω.
По определению ![]() . Тогда существует линия уровня
. Тогда существует линия уровня ![]() проходящая через точку
проходящая через точку ![]() и делящая область
и делящая область ![]() , причем в каждом из частей функция
, причем в каждом из частей функция ![]() принимает значения разных знаков. Для определенности возьмём
принимает значения разных знаков. Для определенности возьмём
![]() .
.
Области ![]() также являются размеченными. Для исследования асимптотического поведения функции (3) при
также являются размеченными. Для исследования асимптотического поведения функции (3) при ![]() для (3) выберем пути интегрирования.
для (3) выберем пути интегрирования.
Пусть состоит из части ![]() соединяющего точки
соединяющего точки ![]() и части линии уровня
и части линии уровня ![]() c соединяющего точки
c соединяющего точки ![]() .
.
Линии уровня функций ![]() являются аналитическими кривыми и их уравнения можно параметризовать по их длине.
являются аналитическими кривыми и их уравнения можно параметризовать по их длине.
Длину линии ![]() от точки
от точки ![]() обозначим s, а длину линии
обозначим s, а длину линии ![]() от точки
от точки ![]() обозначим σ.
обозначим σ.
Учитывая выбранные пути интегрирования и параметры, функцию (3) перепишем в следующем виде
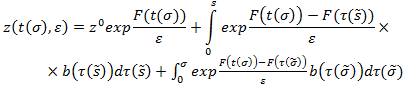 (4)
(4)
Рассмотрим следующие случаи:
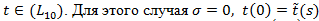 и (4) имеет вид
и (4) имеет вид
![]() . (5)
. (5)
К интегралу, в (5), применяя метод стационарной фазы, получим, что он имеет порядок ε. В рассматриваемом случае
![]() .
.
Таким образом ![]() функция (5) не имеет предела при
функция (5) не имеет предела при ![]() , но ограничена по модулю т.е.
, но ограничена по модулю т.е.
![]() ,
,
где ![]() – постоянная не зависящая от ε.
– постоянная не зависящая от ε.
- Пусть
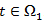 . В этом случае для значений
. В этом случае для значений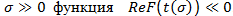 . Следовательно, в (4) первое и второе слагаемое бесконечна мала по сравнению с ε, а третье слагаемое имеет порядок ε (надо учесть, что
. Следовательно, в (4) первое и второе слагаемое бесконечна мала по сравнению с ε, а третье слагаемое имеет порядок ε (надо учесть, что 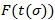 убывает). Таким образом для
убывает). Таким образом для 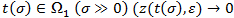 .
. - Пусть
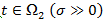 .
.
Для асимптотической оценка ![]() воспользуемся неравенством
воспользуемся неравенством ![]()
Из (4) получим
![]() (6)
(6)
К первому интегралу в (6) применим метод стационарной фазы, тогда
![]() ,
,
где ![]() - постоянная не зависящая от ε; для второго интеграла применяя метод интегрирование по частям получим оценку.
- постоянная не зависящая от ε; для второго интеграла применяя метод интегрирование по частям получим оценку.
![]() ,
,
где ![]() - постоянная не зависящая от ε.
- постоянная не зависящая от ε.
Учитывая полученные оценки, для ![]() имеем
имеем
![]() .
.
Отсюда следует, для ![]() .
.
Таким образом часть области ![]() является областью притяжения вырожденного уравнения [1], [2].
является областью притяжения вырожденного уравнения [1], [2].
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы\ References
- Алыбаев К.С. Метод линий уровня исследования сингулярно возмущенных уравнений при нарушении условия устойчивости / К.С. Алыбаев //Вестник КГНУ. – Серия 3, Выпуск 6. – Бишкек, 2001г. – С. 190-200.
- Панков П.С. Явление погранслойных линий и асимптотика решений сингулярно возмущенных линейных обыкновенных дифференциальных уравнений с аналитическими функциями / Панков П.С., Алыбаев К.С., ТампагаровК.Б. и др. // Вестник ОшГУ, 2013-№1 (специальный выпуск). – С. 227-231.
- Тампагаров К.Б. Погранслойные линии для сингулярно и регулярно возмущенных дифференциальных уравнений первого порядка с аналитическими функциями / К.Б. Тампагаров // Естественные и математические науки в современном мире: сб. статей по материалам XLVII международной научно-практической конференции. №10 (45). Россия, Новосибирск: СиБАК, 2016. –С. 67-73.
- Алыбаев К.С. Явление простирающегося симметричного пограничного слоя для сингулярно возмущенных уравнений при потере устойчивости / Алыбаев К.С., Нарбаев М.Р. // Вестник ЖАГУ. Жалал-Абад, 2008. №1. – с.122-126.
- Алыбаев К.С. // Исслед. по интегро-дифферен. Уравнениям / Алыбаев К.С., Нарбаев М.Р. // Выпуск 35. Бишкек. 2006. С. 105 – 109
- Алыбаев К.С. Сингулярно возмущенные уравнения с аналитическими функциями теряющие единственность при вырождении / К.С. Алыбаев, А.Б.Мурзабаева // Итоги науки в теории и практике 2017: сб. статей по материалам XXXIV международной научной конференции. № 12 (34) Россия, Москва: ЕНО, 2017. – С.15-20.
- Мурзабаева А.Б. Системы сингулярно возмущенных обыкновенных дифференциальных уравнений с аналитическими функциями теряющие единственность при вырождении / А.Б. Мурзабаева // Теоретические и практические вопросы современной науки: сб. статей по материалам XLI международной научной конференции. № 7 (41) Россия, Москва: ЕНО, 2018. –С.12- 18.
- Alybayev K.S. Singularly perturbed first-order equations in complex domains that lose their uniqueness under degeneracy / К.S. Alybaev, A.B Murzabaeva // International conference on analysis and applied mathematics (icaam 2018) AIP Conference Proceedings Volume number: 1997, 020076, Aug 6 (2018); org/10.1063/1.5049070.
- Мурзабаева А.Б. Нарушение единственности решений вырожденного уравнения для сингулярно возмущенных уравнений с аналитическими функциями / А.Б. Мурзабаева // Информационные технологии и математическое моделирование в науке, технике и образовании. № 3 (39) часть 1 Кыргызстан, Бишкек: “Текник”2016.-С.162-169.
- Мурзабаева А.Б. Сингулярно возмущенные уравнения при нарушении единственности решений вырожденного уравнения и условия устойчивости // Естественные и математические науки в современном мире:сб.ст.по матер. XLIX междунар.науч.-практ. конф.№12(47).- Нобосибирск : Сибак, 2016.-С.77-85.
Список литературы на английском языке / References in English
- Alybaev K.S. Metod linii urovnya issledovaniya singuliarno vozmushchennykh uravnenii pri narushenii usloviya ustoichivosti [Method of Level Lines for Study of Singularly Perturbed Equations in Violation of Stability Condition] / K.S.Alybaev // Bulletin of KSNU. – Series 3, Issue 6. – Bishkek, 2001. – P. 190-200. [in Russian]
- Pankov P.S. Yavlenie pogransloinykh linii i asimptotika reshenii singuliarno vozmushchennykh lineinykh obyknovennykh differentsialnykh uravnenii s analiticheskimi funktsiyami [Phenomenon of Boundary Layer Lines and Asymptotics of Solutions of Singularly Perturbed Linear Ordinary Differential Equations with Analytic Functions] / PankovS., Alybaev K.S., Tampagarov K.B. and others // Bulletin of Osh State University, 2013-No.1 (special issue). – P. 227-231. [in Russian]
- Tampagarov K.B. Pogransloinye linii dlia singuliarno i reguliarno vozmushchennykh differentsialnykh uravnenii pervogo poriadka s analiticheskimi funktsiyami [Boundary Lines for Singularly and Regularly Perturbed First-Order Differential Equations with Analytic Functions] / K.B. Tampagarov // Yestestvennyye i matematicheskiye nauki v sovremennom mire: kolledzh. statey o materialakh XVI Mezhdunarodnoy nauchno-prakticheskoy konferentsii. [Natural and Mathematical Sciences in Modern World: Coll. of Articles on the Materials of the XLVII International Research-to-Practice Conference]. No.10 (45). Russia, Novosibirsk: SiBAK, 2016. – 67-73. [in Russian]
- Alybaev K.S. Yavlenie prostirayushchegosia simmetrichnogo pogranichnogo sloya dlia singuliarno vozmushchennykh uravnenii pri potere ustoichivosti [Phenomenon of Extending Symmetric Boundary Layer for Singularly Perturbed Equations with Loss of Stability] / Alybaev K.S., Narbaev M.R. // Herald of JASU. Jalal-Abad, 2008. No.1. - p.122-126. [in Russian]
- Alybaev K.S. // Issled. po integro-differen. uravneniyam. [Study of Integro-different. Equations] / Alybaev K.S., Narbaev M.R. // Issue 35. Bishkek. 2006. P. 105 – 109 [in Russian]
- Alybaev K.S. Singuljarno vozmushchennye uravneniya s analiticheskimi funktsiyami teriayushchie edinstvennost pri vyrozhdenii [Singularly Perturbed Equations with Analytic Functions that Lose Uniqueness under Degeneracy] / K.S. Alybaev, A.B. Murzabaeva // Rezul'taty nauki v teorii i praktike 2017: Kolledzh. statey o materialakh XXXIV Mezhdunarodnoy nauchnoy konferentsii. № 12 (34) [Results of Science in Theory and Practice 2017: Colle. of Articles on the Materials of the XXXIV International Scientific Conference. No. 12 (34) Russia, Moscow: ЕNО, 2017. - P.15-20. [in Russian]
- Murzabaeva A.B. Sistemy singuliarno vozmushchennykh obyknovennykh differentsialnykh uravnenii s analiticheskimi funktsiyami teriajyshchie edinstvennost pri vyrozhdenii [Systems of Singularly Perturbed Ordinary Differential Equations with Analytic Functions that Lose Uniqueness under Degeneracy] / B. Murzabaeva // Teoreticheskiye i prakticheskiye voprosy sovremennoy nauki: sb. statey po materialam Mezhdunarodnoy nauchnoy konferentsii XLI [Theoretical and Practical Questions of Modern Science: Coll. of Articles on the Materials of the XLI International Scientific Conference. No. 7 (41)] Russia, Moscow: ЕNО, 2018. – P.12- 18. [in Russian]
- Alybayev K.S. Singularly perturbed first-order equations in complex domains that lose their uniqueness under degeneracy / К.S. Alybaev, A.B Murzabaeva // Mezhdunarodnaya konferentsiya po analizu i prikladnoy matematike (icaam 2018) AIP Conference Proceedings Volume number: 1997, 020076 [International conference on analysis and applied mathematics (icaam 2018) AIP Conference Proceedings Volume number: 1997], 020076, Aug 6 (2018); org/10.1063/1.5049070. [in Russian]
- Murzabaeva A.B. Narushenie edinstvennosti reshenii vyrozhdennogo uravneniya dlia singuliarno vozmushchennykh uravnenii s analiticheskimi funkciyami [Violation of Uniqueness of Solutions of Degenerate Equation for Singularly Perturbed Equations with Analytic Functions] / B. Murzabaeva // Informatsionnyye tekhnologii i matematicheskoye modelirovaniye v nauke, tekhnike i obrazovanii [Information Technologies and Mathematical Modeling in Science, Engineering and Education]. No. 3 (39) part 1 Kyrgyzstan, Bishkek: “Technik” 2016. – P.162-169. [in Russian]
- Murzabaeva A.B. Singuliarno vozmushchennye uravneniya pri narushenii edinstvennosti reshenii vyrozhdennogo uravneniya i usloviya ustoichivosti [Singularly Perturbed Equations in Violation of Uniqueness of Solutions of Degenerate Equation and Stability Condition] // Yestestvennyye i matematicheskiye nauki v sovremennom mire: sbornik statey. XLIX Mezhdunarodnaya nauchno-prakticheskaya konferentsiya [Natural and Mathematical Sciences in Modern World: Collected Articles. XLIX International Research-to-Practice Conf. No. 12 (47)]. – Novosibirsk: Sibak, 2016. – P.77-85. [in Russian]
