ОСОБЕННОСТИ ПОВЕДЕНИЯ ГАЗОЖИДКОСТНОЙ СМЕСИ В ТРУБАХ

ОСОБЕННОСТИ ПОВЕДЕНИЯ ГАЗОЖИДКОСТНОЙ СМЕСИ В ТРУБАХ

Научная статья

Акперли Р.С. *

Азербайджанский университет архитектуры и строительства, Баку, Азербайджан

* Корреспондирующий автор (akbarli89[at]mail.ru)

Аннотация

Экспериментальные и теоретические исследования, проведенные в последнее время с газосодержащими жидкостями, показали, что в предпереходных условиях (т.е. в области давлений, превышающих давление насыщения, но близких к нему) реологические и релаксационные свойства газожидкостных систем во многом определяются наличием «микро зародышей» - мельчайших газовых пузырьков, кооперативное действие которых проявляется при приближении к давлению насыщения [1]. При решении многих практических задач возникает необходимость изучения распространения волн с учетом влияния взаимодействия между жидкостью и стенкой деформируемой трубы. В этом случае получается система, состоящая из деформированного тела, жидкости и газа, поэтому исследование следует проводить с учетом сил взаимодействия между деформированным телом, жидкостью и газом.

Ключевые слова: вязко-упругая труба, вязкая жидкость, волны, уравнение дисперсии.

MAIN PROPERTIES OF A GAS-LIQUID MIXTURE IN PIPES

Research article

Akperli R.S. *

Azerbaijan University of Architecture and Construction, Baku, Azerbaijan

* Corresponding author (akbarli89[at]mail.ru)

Abstract

Recently carried out experimental and theoretical studies with gas-containing liquids have shown that rheological and relaxation properties of gas-liquid systems under pre-transition conditions (i.e., in pressures exceeding the saturation pressure, but close to it) are largely determined by the presence of “micro germs” – the smallest gas bubbles, the cooperative action of which manifests itself when approaching the saturation pressure [1]. When solving many practical problems, it becomes necessary to study the wave propagation with regard to the influence of the interaction between the liquid and the wall of the deformable pipe. In this case, the system consisting of a deformed body, liquid, and gas is obtained; therefore, the study should be carried out with regard to the interaction forces between the deformed body, liquid and gas.

Keywords: visco-elastic pipe, viscous fluid, waves, dispersion equation.

Введение

Решая задачу транспорта двухфазных потоков, необходимо иметь в виду, что такая среда отличается от других двухфазных сред тем, что теплоемкость несущей фазы  значительно превышает теплоемкость дисперсной фазы  в силу преобладающего массового содержания несущей фазы в единице объема [2]: . Здесь  соответственно плотности жидкости и газа. В связи с этим жидкость является термостатом и имеет постоянную температуру .

В рамках указанных особенностей представляет теоретический и практический интерес характер течения двухфазной пузырьковой жидкости в цилиндрических трубах. Актуальность этой задачи определяется также и тем, что в инженерной практике (медицина, транспорт и хранение нефти и газа, авиация и т.д.) широко распространены конструкции, составляющие элементы которых, имеют полости или отсеки, содержащие жидкость, которая в свою очередь никогда не бывает однородной, а содержит небольшие добавки нерастворенного газа.

Систему, состоящую из жидкой, газообразной и твердой фаз, моделируем как изотропную, однородную, бесконечную цилиндрическую оболочку.

Предполагается, что движение газожидкостной среды и оболочки осесимметричное. Тогда уравнения движения оболочки в цилиндрической системе координат , где ось  направлена вдоль оси тонкостенной оболочки, радиальная координата, имеют вид [3]:

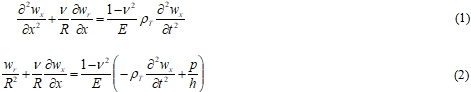
здесь,  - плотность материала оболочки,   - радиальная и продольная координаты вектора перемещений частиц оболочки, t - время, v - коэффициент Пуассона и E - модуль Юнга, R и h соответственно радиус и толщина оболочки, p - давление газожидкостной среды.

На внутренней поверхности оболочки принимается условие равенства радиальных скоростей двухфазной среды и стенки оболочки:

   (3)

Если объемное содержание пузырьков в единице объема смеси   (случай весьма интересный с точки зрения практики) то реализуется устойчивая пузырьковая структура среды и последняя может рассматриваться как некая однородная «пузырьковая жидкость» [4].

Характерной особенностью такой жидкости является высокая средняя

   (4)

плотность, мало отличающаяся от плотности несущей фазы в силу . Здесь нижние индексы 1 и 2 относятся соответственно к параметрам жидкой и газовой фазы. При этом сжатие смеси фактически происходит только за счет сжатия ее газовой составляющей, жидкая фаза практически не сжимается.

Используем общепринятое допущение о проявлении вязкости лишь в процессах межфазного взаимодействия и проявлении в макроскопических процессах переноса импульса.

Предполагаем также, что среднемассовая температура смеси постоянна.

При этих допущениях линеаризованные уравнения неразрывности и движения запишутся в виде:

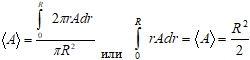Здесь нижний индекс 0 относится к невозмущенному состоянию. Усредним уравнение (5) по сечению трубы. Имея в виду, что получим В дальнейшем учтем, что [5] Из уравнения (8) с учетом (4) получаем    (10) Число пузырьков радиусом в единице объема смеси связано с объемным содержанием пузырьков   соотношением     (11) При отсутствии межфазного массообмена число пузырьков в единице объема удовлетворяет уравнению [6]     (12) Согласно (5) и (12) имеем      (13) Продифференцировав (11) и проведя линеаризацию полученного уравнения, придем к соотношению:       (14) Рассмотрим случай, когда при пульсациях пузырьков радиальная инерция жидкой фазы несущественна, а разница между давлениями фаз уравновешивается вязкими силами в жидкости. Такая ситуация реализуются, когда пузырьки мелкие, а жидкость вязкая [7]. Пренебрегая инерционными членами в уравнении Релея, описывающего закон движения подвижной границы раздела фаз, получим Здесь  коэффициент поверхностного натяжения,  вязкость жидкости. 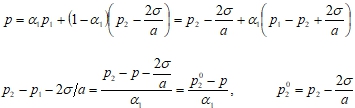Отсюда получаем    (15) Согласно, Подставив последнее соотношение в (15), получим    (16) Подставив (16) и (13) в (14), получим    (17) Подставим (17) в уравнение (10): Откуда следует    (18)

Поскольку скорость звука  в жидкой фазе смеси велика и объемное содержания пузырьков мало, сжимаемостью жидкости можно пренебречь

то уравнение для определения давления в (18) упрощается и принимает вид    (19) Давление  можно определить, рассмотрев уравнение сохранения массы индивидуального пузырька:    (20) Соотношение (20) можно преобразовать к виду   Если учесть уравнение состояния калорически совершенного газа

С учетом (11) и (13) получаем . Из уравнения (4) имеем . Откуда окончательно получаем

Если для простоты пренебречь капиллярными эффектами , то линеаризованное выражение для давления (19) примет вид:

   (21)

Таким образом, полная система уравнений для определения давления смеси принимает вид

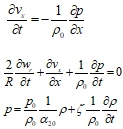
Система уравнения (1), (2) и (22) замкнута и может быть использована для исследования эволюции малых возмущений в оболочке, содержащей газожидкостную среду.

Далее будем использовать следующие безразмерные переменные и параметры:

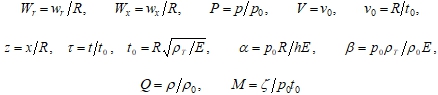Тогда система уравнений в безразмерном виде приобретет вид: 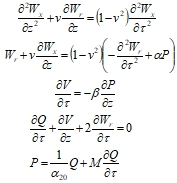   (23)

Рассмотрим случай переменной вязкости жидкости. Вязкость жидкости в значительной степени зависит от температуры и давления. Зависимость вязкости жидкости от давления в широком диапазоне давлений остаётся практически линейной:

   (24)

где:  - вязкость жидкости при атмосферном давлении,  - экспериментальный коэффициент пропорциональности.

Пусть по аналогии с (2) и (9)

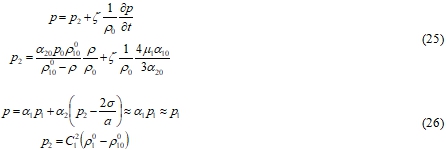Для нелинейной задачи без учета капиллярных сил будем иметь: Для несжимаемой жидкости имеем:

Здесь  и  соответственно давление и плотность газожидкостной среды,  - объемное содержание пузырьков в единице объема смеси  - динамическая вязкость жидкости (для воды  истинная плотность жидкости (для воды при атмосферном давлении ). Нижний индекс «0» относится к значению параметров при .

Вязкость воды примерно в 60 раз больше вязкости воздуха, поэтому при  практически не зависит от объемного содержания пузырьков в смеси.

Заключение

Таким образом, исходя из выбранных параметров и режима работы системы, можно сделать следующие выводы:

• По мере увеличения значения α скорость распространение волны значительно уменьшается;
• Кроме того, амплитуда безразмерной плотности увеличивается на порядок;
• Амплитуда скорости смеси потока (и, следовательно, потребление) увеличивается;
• Выявлено, что только вязкость слегка влияет на характер потока смеси.

Конфликт интересов Не указан.

Conflict of Interest None declared.

 

Список литературы / References

1. Nigmatulin R.I. Multiphase Dynamics / Nigmatulin R.I. V.1, – М., 1987, 464 p.
2. Aliyev G.A. Pulsational flow of a two-phase fluid in a non-uniform visco-elastic pipe due to the effect of constriction / Aliyev G.A. Amenzade R.Y. The News of Bki University, №1, 2005, P. 66-74
3. Akbarly R.S. Waves propagation in the fluid flowing in an elastic tube, considering viscoelastic friction of surrounding medium / Akbarly R.S. International journal on technical and physical problems of engineering 35, 2018, P. 39-42
4. Muhammad B.R. Couette flows of a viscous fluid with slip effects and non-integer order derivative without singular kernel / Muhammad B.R., Muhammad I.A. Discrete and Continuous Dynamical Systems, 12(3), 2018, P. 645-664
5. Umer F. Computational Analysis For Mixed Convective Flows of Viscous Fluids With Nanoparticles / Umer F., Dianchen L., Muhammad R. Journal of Thermal Science and Engineering Applications, 11(2), 2018, P. 92-99
6. Lan H. Global attractor for a nonlinear one-dimensional compressible viscous micropolar fluid / Xin-Guang Y., Yongjin L., Taige W. Mathematik and Physik 1-20, 2018
7. Chen W.Q. On wave propagation in anisotropic elastic cylinders at nanoscale: surface elasticity and its effect / B.Wu, C.L.Zhang, Ch. Zhang. Acta Mech 225, 2014, P. 2743–2760