ОПТИМИЗАЦИЯ ЗЕМЛЕПОЛЬЗОВАНИЯ АПК НА ОСНОВЕ МАТЕМАТИЧЕСКИХ МЕТОДОВ ФИНАНСОВОГО АНАЛИЗА
Сахарова Л.В.1, Стрюков М.Б.2
Ростовский государственный экономический университет (РИНХ)
ОПТИМИЗАЦИЯ ЗЕМЛЕПОЛЬЗОВАНИЯ АПК НА ОСНОВЕ МАТЕМАТИЧЕСКИХ МЕТОДОВ ФИНАНСОВОГО АНАЛИЗА
Аннотация
В статье представлена модель оптимизации нерационального землепользования на основе данных о посевных площадях и урожайности для основных сельскохозяйственных культур, выращиваемых в Ростовской области. В качестве математического анализа для моделирования использованы методы регрессионного анализа и нелинейной оптимизации, обычно применяемые в математических методах финансового анализа для оптимизации портфелей финансовых инструментов. Модель позволяет рассчитать оптимальное количественное распределение территорий, обеспечивающее максимальную среднюю урожайность при минимальном среднем риске.
Ключевые слова: модель оптимизации, агротехническое землепользование, урожайность сельскохозяйственной территории.
Sakharova L.V.1, Stryukov M.B.2
1,2Rostov State University of Economics (RSUE)
OPTIMIZATION OF LAND-USE MANAGEMENT IN AGROINDUSTRIAL COMPLEX BASED ON MATHEMATICAL METHODS OF FINANCIAL ANALYSIS
Abstract
The paper presents the model for minimization of irrational land-use based on the data on crop areas and yields for the main agricultural crops grown in the Rostov Region. The regression analysis and nonlinear optimization methods, commonly used in mathematical methods of financial analysis for the optimization of financial portfolios were used in the mathematical analysis and simulation. The model enables to calculate the optimal quantitative distribution of territories, ensuring a maximum average yield with a minimum average risk.
Keywords: optimization model, agronomic land use, yield of agricultural territory.
Введение
Оптимизация нерационального агротехнического землепользования является одной из приоритетных задач математического моделирования в агропромышленном комплексе. В то же время, математический аппарат в данной области еще недостаточно разработан. Как правило, для моделирования в АПК применяются традиционные статистические и эконометрические методы. Их недостаток заключается в том, что они применимы в локальных условиях и не обладают достаточным уровнем универсальности. В данной статье предложена простая модель, позволяющая оптимизировать землепользование на основе классических методов финансового анализа – так называемой «портфельной теории» [1],[2]. Модель обладает достаточной универсальностью. Для ее применения необходима лишь статистическая информация об урожайности основных сельскохозяйственных культур, выращиваемых на рассматриваемой сельскохозяйственной территории.
- Модификация оптимизационных методов финансового анализа для АПК
Предполагается, что на заданной агропромышленной территории планируется выращивать n сельскохозяйственных культур, урожайность каждой из которых представлена статистической выборкой за некоторый временной период. Пусть ![]() есть подлежащий оптимизации вектор, где xk ∈ R — доля территории, занятой сельскохозяйственной культурой с номером k (k = 1, 2, … , n). Очевидно, что должно выполняться условие:
есть подлежащий оптимизации вектор, где xk ∈ R — доля территории, занятой сельскохозяйственной культурой с номером k (k = 1, 2, … , n). Очевидно, что должно выполняться условие: ![]() . Очевидно, что в отличие от задачи об оптимизации портфеля ценных бумаг, в рассматриваемой задаче значения xk могут быть только положительными. Тогда величина
. Очевидно, что в отличие от задачи об оптимизации портфеля ценных бумаг, в рассматриваемой задаче значения xk могут быть только положительными. Тогда величина ![]() есть урожайность заданной агропромышленной территории; Ek есть урожайность k-й сельскохозяйственной культуры (случайная величина). Тогда средней ожидаемой урожайностью агропромышленной территории будем называть математическое ожидание величины Еx, а риском – ее среднеквадратическое отклонение. Будем минимизировать риск при заданной средней урожайности r. Опуская подробные выкладки (аналогичные тем, что производятся в математических методах финансового анализа для задачи минимизации риска портфеля финансовых инструментов при его заданной доходности) сформулируем задачу оптимизации сельскохозяйственного землепользования:
есть урожайность заданной агропромышленной территории; Ek есть урожайность k-й сельскохозяйственной культуры (случайная величина). Тогда средней ожидаемой урожайностью агропромышленной территории будем называть математическое ожидание величины Еx, а риском – ее среднеквадратическое отклонение. Будем минимизировать риск при заданной средней урожайности r. Опуская подробные выкладки (аналогичные тем, что производятся в математических методах финансового анализа для задачи минимизации риска портфеля финансовых инструментов при его заданной доходности) сформулируем задачу оптимизации сельскохозяйственного землепользования:
![]() (1)
(1)
![]() (2)
(2)
где xk есть доля территории, занятой k-й сельскохозяйственной культурой; ![]() – ожидаемая средняя урожайность k-й сельскохозяйственной культуры (k =1, … , n), вычисляемая как выборочное среднее значение для случайной величины
– ожидаемая средняя урожайность k-й сельскохозяйственной культуры (k =1, … , n), вычисляемая как выборочное среднее значение для случайной величины ![]() – ковариация урожайностей k-й и
– ковариация урожайностей k-й и
- Оптимизация сельскохозяйственных территорий Ростовской области
Оптимизацию агропромышленных территорий Ростовской области осуществим в четыре этапа, в соответствии с количественными и качественными характеристиками статистической информации об урожайности [3].
1 этап. Рассмотрим подробно оптимизацию территорий на основе разделения сельскохозяйственной продукции по четырем основным видам: зерновые культуры, подсолнечник, картофель, овощи. Следующие показатели за 1990-2015 гг представлены для каждого вида культур: посевная площадь (тыс. га), валовый сбор сельскохозяйственной продукции (тыс. тонн), урожайность (цн/га). Данная статистическая информация сведена в Таблицы 1,2.
Внизу таблиц приведены также результаты первоначальной статистической обработки выборок. Это средние значения случайных величин (посевная площадь, валовый сбор, урожайность) M, квадраты среднеквадратических отклонений σ2, а также сами среднеквадратические отклонения σ. Для удобства эконометрического анализа сельскохозяйственным культурам присвоена следующая нумерация: зерновые культуры – №1; подсолнечник – №2; картофель – №3; овощи – №4.
Из таблиц следует, что средние урожайности четырех видов с/х культур равны: r1= 22.457143; r2= 11.285714; r3= 97.342857; r4 =119.961905.
Используя средние значения площадей (отведенных под каждую из четырех сельскохозяйственных культур) найдем соответствующую среднюю суммарную площадь используемой агропромышленной территории:
S=S1 + S2 + S3 + S4 = 2704.72000 + 891.43000 + 45.19 + 40.58000 = 3681.92.
Соответственно, средние доли площадей, занятые под каждой вид культуры, равны: X1 =0.73459; X2 =0.24211; X3 =0.01227; X4 =0.01102. Следовательно, средняя урожайность агропромышленной территории, используемой под рассматриваемые четыре вида сельскохозяйственных культур в Ростовской области, в соответствии с представленными статистическими данными, равна: rср=r1 * X1 + r2 * X2 + r3 * X3+ r4 * X4 = 21.28. Средний риск, полученный на основе обработки исходных статистических данных, равен 34%.
Таблица 1 – Статистические данные для зерновых культур и подсолнечника
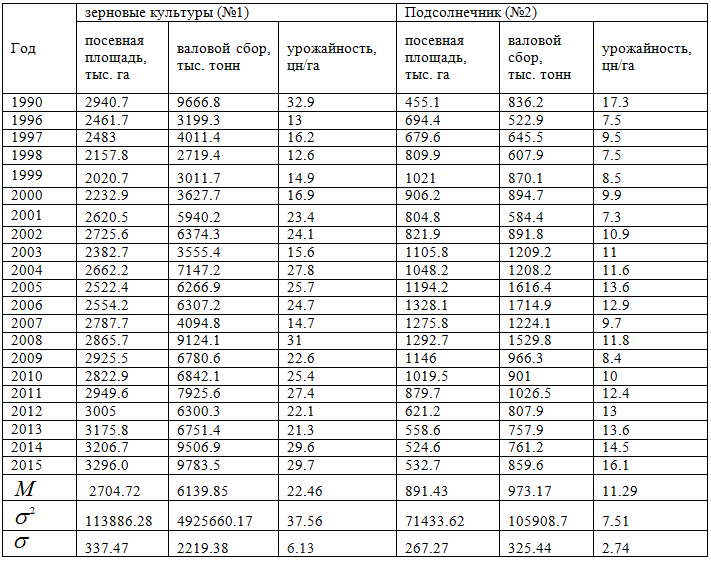
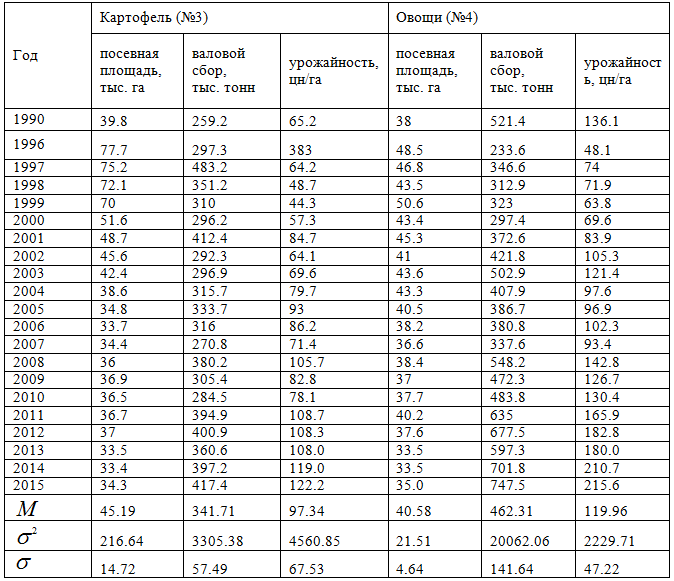
Таблица 2 – Статистические данные для картофеля и овощей
Задача об оптимизации территорий для четырех культур, как следует из общей формулировки задачи (1) – (2), имеет вид:
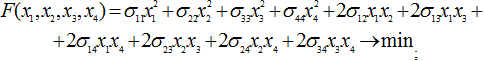 (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
Применив к выборкам регрессионный анализ, получим значения ковариации, а также коэффициентов корреляции урожайностей рассматриваемых четырех видов сельскохозяйственных культур и построим задачу нелинейного программирования для четырех основных видов сельскохозяйственных культур в Ростовской области. Решим задачу для различных значений средней ожидаемой урожайности, использовав метод множителей Лагранжа, а также условия Куна-Такера [3],[4] (см.Таблицу 3).
Таблица 3 – Результаты оптимизационных расчетов, первый этап
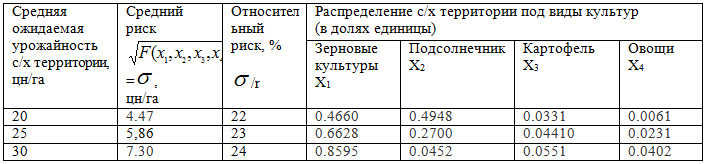
Расчеты показывают, что средняя ожидаемая урожайность r =35 недостижима, поскольку среди компонент решения присутствуют отрицательные. Как можно видеть из таблицы, риск при оптимальном распределении территорий не превышает 24% против 34% при среднем исходном (статистическом) распределении агропромышленных территорий. В то же время, численный эксперимент указывает на то, что можно достигнуть средней ожидаемой урожайности территории 30 цн/га при риске 24% против статистической средней урожайности 21,28 цн/га при среднем риске 34%.
2 этап. На втором этапе оптимизируем территории, отведенные под зерновые культуры, по четырем их основным видам, существенно различающимся по агротехническим характеристикам: озимые зерновые культуры – №1; яровые зерновые культуры – №2; рис – №3; зернобобовые – №4. Для каждого вида культур имеются следующие показатели за 2000-2015 гг: посевная площадь (тыс. га), валовый сбор сельскохозяйственной продукции (тыс. тонн), урожайность (цн/га). Статистический анализ показывает, что средние урожайности четырех видов зерновых культур равны: r1= 27.74; r2= 17.17; r3=39.73; r4 =16.45. Суммарная средняя территория, отведенная под зерновые культуры, равна: S=2725.35. Средние доли, занятые видами культур, равны: X1= 0.632, X2= 0.338, X3= 0.005, X4= 0.025. Средняя урожайность равна: rср= 23.95. Как следует из результатов 1-го этапа, средний риск агропромышленных территорий, занятых зерновыми культурами, равен 6.13, то есть относительный риск территории равен 25,6%. Результаты оптимизационных расчетов приведены в Таблице 4.
Таблица 4 – Результаты оптимизационных расчетов, второй этап
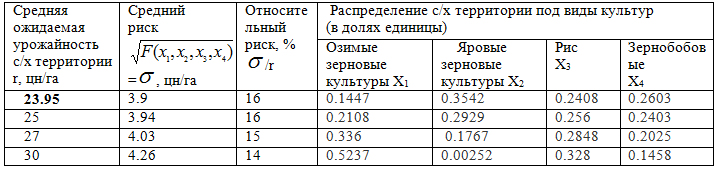
Как можно видеть из таблицы, риск при оптимальном распределении территорий не превышает 16% против 25,6% при среднем исходном (статистическом) распределении агропромышленных территорий. В то же время, численный эксперимент указывает на то, что можно достигнуть средней ожидаемой урожайности территории 30 цн/га при риске 14% против статистической средней урожайности 23,95 цн/га при среднем риске 25,6%.
3 этап. На третьем этапе оптимизируем территории внутри видов зерновых культур. Распределение озимых зерновых будем оптимизировать для трех культур: пшеница, ячмень, рожь (соответственно, №1,2,3 внутри группы озимых). Распределение яровых культур выполним для четырех культур: пшеница, ячмень, кукуруза на зерно и просо (соответственно, №1,2,3,4 внутри группы яровых). Статистический анализ осуществлен для данных о посевной площади (тыс. га) и урожайности (цн/га) за 2000-2015 гг для каждой отдельной культуры. Анализ показывает, что доли, занятые озимыми культурами, равны: X1=0.976, X2=0.016, X3=0.008; средняя урожайность 27.74, а риск равен 5.23, что составляет 19%. Доли, занятые яровыми культурами, соответственно, равны: X1=0.012, X2=0.678, X3=0.188, X4=0.122; средняя урожайность 17.17, а риск равен 4.4, что составляет 26%.
Приведем расчетные оптимизационные данные для рассматриваемых двух групп в Таблицах 5,6. Как следует из Таблицы 5, среднюю ожидаемую урожайность озимых зерновых можно повысить за счет оптимизации распределения территорий до 28 цн/га при риске 18% против 27.74 цн/га при риске 19%. Из Таблицы 6 следует, что среднюю ожидаемую урожайность яровых культур можно повысить до 17.18 цн/га при 24% риска против 17.17 при 26% риска. Дальнейшее улучшение результатов в данных группах невозможно в силу неравномерности распределения культур по средней урожайности.
Таблица 5 –Результаты оптимизационных расчетов, третий этап, 1-я группа
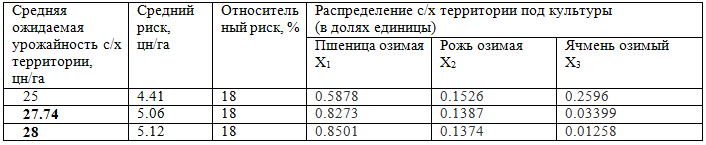
Таблица 6 – Результаты оптимизационных расчетов, третий этап, 2-я группа
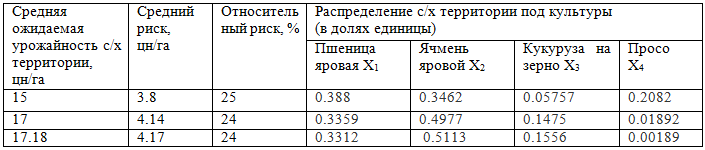
- Расчет оптимизированного распределения территорий на 2018 год
Рассмотрим применение полученных результатов для расчетов распределения агротехнических территорий. Предположим, что суммарная агротехническая территории Ростовской области в 2018 году составит 4000 тыс. га. Тогда, в соответствии с полученными результатами (см. Таблица 3), средняя ожидаемая урожайность территории 30 цн/га при среднем относительном риске 24% может быть достигнута при следующем распределении площадей:
| Зерновые культуры: | S1=4000*0.8595=3438 (тыс. га); |
| Подсолнечник: | S2=4000*0.0452=180.8 (тыс. га); |
| Картофель: | S3=4000*0.0551=220.4 (тыс. га); |
| Овощи: | S4=4000*0.0402=160.8 (тыс. га). |
Внутри группы зерновых культур средняя ожидаемая урожайность территории 30 цн/га при среднем относительном риске 14% может быть достигнута при следующем распределении (см. Таблица 4):
| Озимые зерновые культуры: | S11=3438*0.5237=1800.4806 (тыс. га); |
| Яровые зерновые культуры: | S12=3438*0.0025=8.6638 (тыс. га); |
| Рис: | S13=3438*0.328=1127.6640 (тыс. га); |
| Зернобобовые: | S14=3438*0.1458=501.2604 (тыс. га). |
Внутри группы озимых зерновых культур урожайность территории 28 цн/га при среднем относительном риске 18% может быть достигнута за счет следующего распределения территории между культурами (см. Таблица 5):
| Пшеница озимая: | S111=1800.4806*0.8501=1530.5886 (тыс. га); |
| Рожь озимая: | S112=1800.4806*0.1374=247.3860 (тыс. га); |
| Ячмень озимый: | S113=1800.4806*0.0126=22.6861 (тыс. га); |
Внутри группы яровых зерновых культур средняя ожидаемая урожайность территории 17 цн/га при среднем относительном риске 24% может быть достигнута за счет следующего распределения агротехнических территорий (см. Таблица 6):
| Пшеница яровая: | S121=8.6638 *0.3359= 2.9102 (тыс. га); |
| Ячмень яровой: | S122=8.6638 *0.4977=4.3120 (тыс. га); |
| Кукуруза на зерно: | S123=8.6638 *0.1475=1.2780 (тыс. га); |
| Просо: | S122=8.6638 *0.01892=0.1639 (тыс. га). |
Таблица 7 – Итоговые результаты оптимизационных расчетов
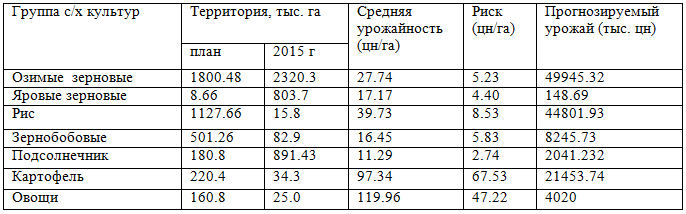
Как можно видеть из таблицы, результаты применения предложенной методики указывают на целесообразность увеличения площадей отведенных под выращивание овощей более чем в 6 раз, картофеля – почти в 7 раз, зернобобовых – 6 раз, риса – почти в 8 раз; вместе с этим, предлагается существенно сократить посевы яровых культур, обладающих относительно низкой урожайностью, в весовом отношении (почти в 10 раз). Кроме того, метод указывает на необходимость в целях оптимизации сократить посевы «легкого» подсолнечника почти в 5 раз. Также предлагается сократить посевы озимых зерновых культур в пользу более «весомых» овощей и картофеля. Кроме того, не учитывалась «весомость» различных типов сельскохозяйственных культур (например, подсолнечник и картофель «весили» в модели одинаково, что и привело к существенному сокращению доли подсолнечника). Отмеченные моменты позволяют сделать вывод, о том, что модель может быть с успехом применена в отношении «равновесомых» сельскохозяйственных культур. Однако при расчетах для разнородных агрокультур их необходимо относить к среднестатистической оптимальной урожайности.
Выводы
Предложена математическая модель оптимизации землепользования, основанная на «портфельной» теории – одном из основных инструментов оптимизации портфелей ценных бумаг в классических математических методах финансового анализа. Для расчетов на основе модели необходимы статистические выборки достаточного объема об урожайности основных сельскохозяйственных культур на оптимизируемой сельскохозяйственной территории. Модель, в целом, позволяет рассчитать оптимальное распределение территорий под посадку как основных групп сельскохозяйственных культур (зерновые, подсолнечник, картофель, овощи и т.д), так и видов внутри группы (озимые и яровые зерновые, рис, зернобобовые), а также конкретных зерновых культур. Расчеты показывают, что оптимальное распределение с/х территорий, рассчитанное на основе модели, позволяет повысить среднюю ожидаемую урожайность территорий при минимизации среднего риска.
Однако для практического применения модели является целесообразным относить урожайности агрокультур к их среднестатистическим оптимальным значениям, чтобы исключить фактор «различия весомости» разнородных агрокультур (например, овощи и подсолнечник).
Кроме того, для приведения модели в соответствие существующим квотам на производство сельскохозяйственной продукции, в нее необходимо в дальнейшем включить дополнительные ограничения по различным видам сельскохозяйственных культур.
Список литературы / References
- Арсеньев, Ю.Н. Управление рисками / Ю.Н. Арсеньев.- М.: Высш. шк., 2007. - 420 с.
- Соловьев, В.И. Математические методы управления рисками: учеб. пособие для студентов всех специальностей / В.И. Соловьев.- М.: ГУУ, 2009.- 98 с.
- Онлайн-калькулятор «Методы оптимизации» [Электронный ресурс]. – URL: http://math.semestr.ru (дата обращения: 20.03.2017).
- Online-сервисы по высшей математике [электронный ресурс]. – URL: http://www.math-pr.com (дата обращения: 15.03.2017).
Список литературы на английском языке / References in English
- Arsenyev Yu. N. Upravlenie riskami [Risk management] / Yu. N. Arsenyev. – M.: Vyssh. wk., 2007. - 420 p. [in Russian].
- Soloviev V. I. Matematicheskie metody upravlenija riskami: ucheb.posobie dlja studentov vseh special'nostej [Mathematical methods for risk management: textbook. a manual for students of all disciplines] / V.I. Solovyov. – M.: GUU, 2009. – 98 p. [in Russian].
- Onlajn-kal'kuljator «Metody optimizacii» [Online calculator «Methods of optimization»] [Electronic resource]. – URL: http://math.semestr.ru (accessed: 20.03.2017). [in Russian]
- OnLine-servisy po vysshej matematike [OnLine services for higher mathematics] [Electronic resource]. – URL: http://www.math-pr.com (accessed: 15.03.2017). [in Russian]
