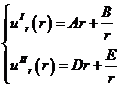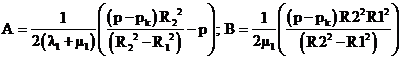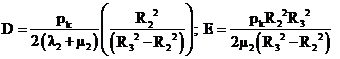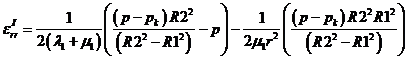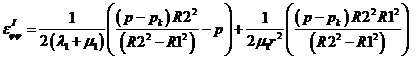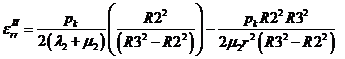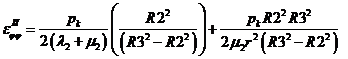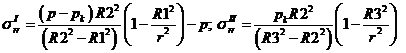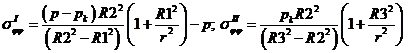ОПРЕДЕЛЕНИЕ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ДВУХСЛОЙНОЙ ТРУБЫ
Блинов А.В.
Студент, Пермский национальный исследовательский политехнический университет
ОПРЕДЕЛЕНИЕ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ДВУХСЛОЙНОЙ ТРУБЫ
Аннотация
В статье сформулирована постановка задачи линейной теории упругости для определения напряженно-деформированного состояния трубы, продемонстрирован алгоритм получения зависимости напряжений и деформаций по радиусу трубы.
Ключевые слова: напряжения, деформация, двухслойная труба.
Blinov A.V.
Student, Perm National Research Polytechnic University
DETERMINATION OF STRESS-STRAIN STATE OF TWO-LAYER PIPES
Abstract
In the article the problem of linear elasticity theory to determine the stress-strain state, demonstrated algorithm for produce according to the stresses and strains along the radius of the tube is formulated.
Keywords: stress, strain, two-layer pipes.
При постановке задачи были внесены следующие упрощения: слои трубопровода – однородные, давление равномерно распределено по внутренней поверхности трубы, внешний слой не имеет гофрированной структуры. В силу данных упрощений можно считать, что задача является осесимметричной и относится к классу плоских задач теории упругости, поэтому удобно рассматривать её решение в цилиндрической системе координат. Внешний и внутренний радиус задаются из условий требуемой задачи, рассматриваемой инженером. Выберем систему координат таким образом, чтобы её начало совпадало с центром тяжести какого-либо произвольного поперечного сечения, а ось Oz была сонаправлена оси симметрии трубы, см. рис 1.
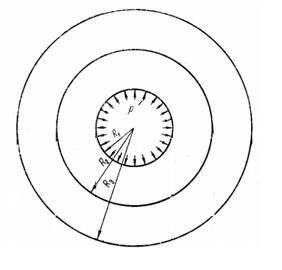Рис. 1. Выбор оси Oz в центре сечения, указание радиусов слоёв трубы и внутреннего давления.
Математическая постановка:
- Уравнение равновесия, применяемое для описания поведения трубы в цилиндрической системе координат:
(1)
- Физические соотношения в цилиндрической системе координат:
; 
(2)
- Геометрические соотношения (связь тензора деформаций от перемещений по радиусу):
; 
(3)
- Граничные условия (4):
Напряжение на внутренней поверхности первого слоя (от центра сечения трубы) определяется через внутреннее давление:
; (4а)
По условиям поставленной задачи, давление на внешнем слое трубы отсутствует, следовательно, напряжение на внешнем радиусе отсутствует:
; (4б)
Учет напряжений между слоями трубы:
; (4в)
Учет перемещений между слоями трубы:
(4г)
где 
- радиальная и угловая координаты. 
- радиальное и окружное напряжения на внутренней и внешней трубе. 
- радиальная и окружная компоненты тензора деформаций. 
- упругие постоянные Ляме изотропного материала. 
- радиальное перемещение на внутренней и внешней трубе. 
- межтрубное давление, действующее на поверхности соприкосновения труб (которое найдется в процессе решения поставленной задачи).
Будем решать задачу в перемещениях в радиальном направлении. В данном случае это удобно, так как постановка плоской осесимметричной задачи включает только одно уравнение равновесия, а поле перемещений является чисто радиальным.
В случае плоского деформированного состояния в теле обязательно возникает ненулевое осевое напряжение 
. Здесь 
- коэффициент Пуассона для материала.
Подставляя соотношения (2) и (3) в уравнение равновесия (1) получим уравнение равновесия в перемещениях в виде:
(5)
Отметим, что уравнения равновесия для первого и второго слоя трубы совпадают на качественном уровне, отличаются лишь свойством материала слоя.
Интегрируя уравнение (5), получим поле перемещений для первого и второго слоя трубы в радиальном направлении:
(6)
Константы A,B,D,E определим из граничных условий задачи (4):
(7)
(8)
Подставим соотношение (6) - (8) в соотношения (3), получим выражения для нахождения напряжений и деформаций для каждого слоя трубы, выраженных через внешний и внутренний радиус, равномерное внутреннее давление и упругие константы:
- Деформации в радиальном направлении по радиусу от внутреннего давления в первом слое трубы:
(9)
- Деформации в окружном направлении по радиусу от внутреннего давления в первом слое трубы:
(10)
- Деформации в радиальном направлении по радиусу от внутреннего давления во втором слое трубы:
(11)
- Деформации в окружном направлении по радиусу от внутреннего давления во втором слое трубы:
(12)
- Напряжение в радиальном направлении по радиусу от внутреннего давления в первом и втором слое трубы:
(13)
Напряжение в окружном направлении по радиусу от внутреннего давления в первом и втором слое трубы:
(14)
По зависимостям (9)-(14) можно однозначно определить напряжения и деформации от радиуса по всему сечению бесконечной двухслойной трубы. Давление на стыке слоев трубы определяется . Ожидается небольшой скачок напряжений и деформаций на стыке слоев бесконечной двухслойной трубы, связанный с контактом между двух материалов.
Данные результаты будут использоваться для проверки применения конечно-элементной модели двухслойного трубопровода, которые используются в различных сферах промышленности. Необходимо построить функциональную зависимость напряжений, деформаций и перемещений от радиуса, меняющегося от внутреннего слоя до внешнего радиуса второго слоя. А так же определить относительную и абсолютную погрешность между аналитическим решением и решением, полученным с помощью метода конечных элементов.
Необходимость применения конечно-элементной модели связано с удобством быстрого определения напряжений и деформаций двухслойной толстостенной трубы, которые применяются для подземной прокладки систем отвода канализационной и дождевой воды, а так же прочих нужд, которые допускает данный тип материала и конструкцию труб. Чаще всего это трубы городской наружной канализации, прежде всего в качестве коллекторов. Могут применяться для строительства канализационных сетей санитарно-технического, ливневого и общего назначения, а благодаря высокой химической стойкости могут успешно использоваться в строительстве промышленных сетей [1].
Литература
- Трубы ПЭ, ПП для наружной канализации двухслойные «ПОЛИТЭК-3000», «FD ПЛАСТ», «POLYTRON». [Электронный ресурс]. URL: http://www.rtg-company.ru/gl/katalog-ceni/details/16/8/narugnie-sistemi-truboprovodov/kanalizatsiya/dvuhsloynaya-
- Демидов С.П. Теория упругости: Учебник для вузов. – М.: Высшая школа, 1979. – 432 с.
- Дарков, А.В. Сопротивление материалов / А.В. Дарков, Шапиро Г.С. – М.: Высшая школа. 1975. – 654 с.
References
- Trubi PE, PP dlya narujnoy kanalizacii dvuhsloynie «politek-3000», «FD plast», «POLYTRON». [electronic resource]. URL: http://www.rtg-company.ru/gl/katalog-ceni/details/16/8/narugnie-sistemi-truboprovodov/kanalizatsiya/dvuhsloynaya-
- Demidov S.P. Teoriya uprugosti: Uchebnik dlya vuzov. – M.: Visshaya shkola, 1979. - 432 s.
- Darkov A.V. Soprotivlenie materialov / A.V. Darkov, Shapiro G.S. – M.: Visshaya shkola. 1975. – 654 s.